10. NP-Completeness

约 4422 个字 2 行代码 预计阅读时间 22 分钟

10.1 概述

根据问题的难度，由不同的定义划分，问题可以分为：

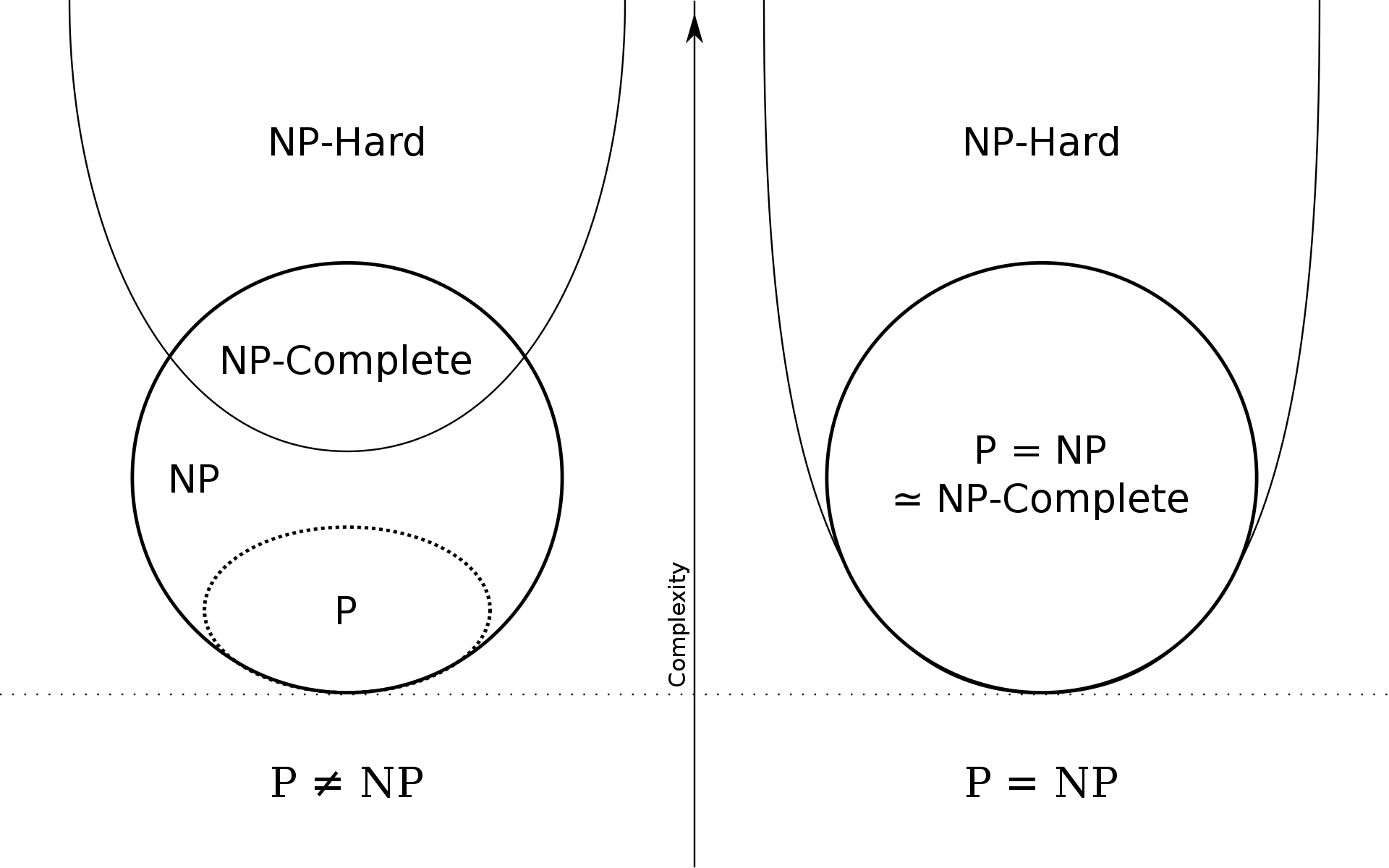
P 问题(polynomial time)、NP 问题(nondeterministic polynomial time)、NPC 问题(NP complete)、NPH 问题(NP hard)。除此之外 ，我们还需要额外了解不可计算问题(undecidable)。

• P 取自 polynomial time，指的是可以用确定型图灵机（指某一指令执行完成之后，下一条指令是唯一确定的）🔍在多项式时间内解决的问题。

也就是我们通常意义下所说的，可以在多项式时间内解决的问题。

• NP 即 nondeterministic polynomial time，指的是可以用[非确定型图灵机（在某一条指令执行完成之后，下一条指令可以有若干个，机器总能选出正确的一条）🔍]在多项式时间内解决的问题。这个说法等价于可以用[确定型图灵机🔍]在多项式时间内验证（判断答案是否正确）。

也就是我们通常意义下所说的，可以在多项式时间内验证的问题。

• NPC 即 NP complete，NP 完全，是 NP 中最难的决定性问题（并不是无限定词的最难的问题！）。而我们称满足如下条件的问题为 NPC 问题：

• 是一个 NP 问题；

• 所有 NP 问题都可以[多项式时间归约🔍]为该问题；

由 2 可以有结论，所有的 NPC 问题难度相同——一旦有一个 NPC 问题被解决，那么所有 NPC 问题，乃至所有 NP 问题都能被解决。

如果我们试图证明一个问题是 NPC 问题，我们可以通过这种手段：

1. 判定该问题是一个 NP 问题；

2. 判定一个已知的 NPC 问题可以[多项式时间归约🔍]为该问题，或判定该问题是 NPH（在下面）问题；

   NPC问题难度相同，NPC问题能够归约到另一个NPC故事。或者利用\(NPC = NP \cap NPH\),如果一个既是NP问题，又是NPH问题，那么它也是NPC问题

第一个被证明是 NPC 的问题是 [Circuit-SAT🔍] 问题。

• NPH 即 NP hard，NP 困难，它不一定需要是 NP 问题。而所有 NP 问题都可以[多项式时间归约🔍]为 NPH 问题。

NPH问题无法通过不确定图灵机进行验证

all the language can be decided by a non-deterministic machine。 F

$$ NPC = NP \cap NPH $$

10.2 Undecidable Problem

不可判定问题(undecidable problem)是一类特殊的决定性问题，它的特点是我们无法设计一个算法来求解它的结果。

停机问题是一个典型的不可计算问题，它指的是，对于任意一个程序，我们无法设计一个算法来判断它是否会在有限时间内停机（即判断程序是否会死循环）。

我们通过反证法可以证明：

假设存在函数 willHalt(func F) 可以判断函数 F 是否会停机，如果会，则返回 true，否则返回 false。那么我们可以构造一个这样的函数 foo()：

void foo() {
    if ( willHalt(foo) ) {
        while (true) {} // Endless loop.
    }
    return;
}

接下来，如果我们想知道 foo() 是否会停机，就会执行 willHalt(foo)。然而在 foo() 内部也有一个 willHalt(foo)，如果它认为 foo() 会停机，则构造一个死循环；而如果它认为 foo() 不会停机，则选择让它立刻停机，于是这里就产生了矛盾。

理解上面这段内容的关键就是，这里虽然不存在事实意义上的“死循环”，但可以理解为这里存在一个逻辑上的递归，而这种“逻辑上的递归”，正是导致停机问题成为一个不可计算问题的原因。

10.3 P 问题 和 NP 问题

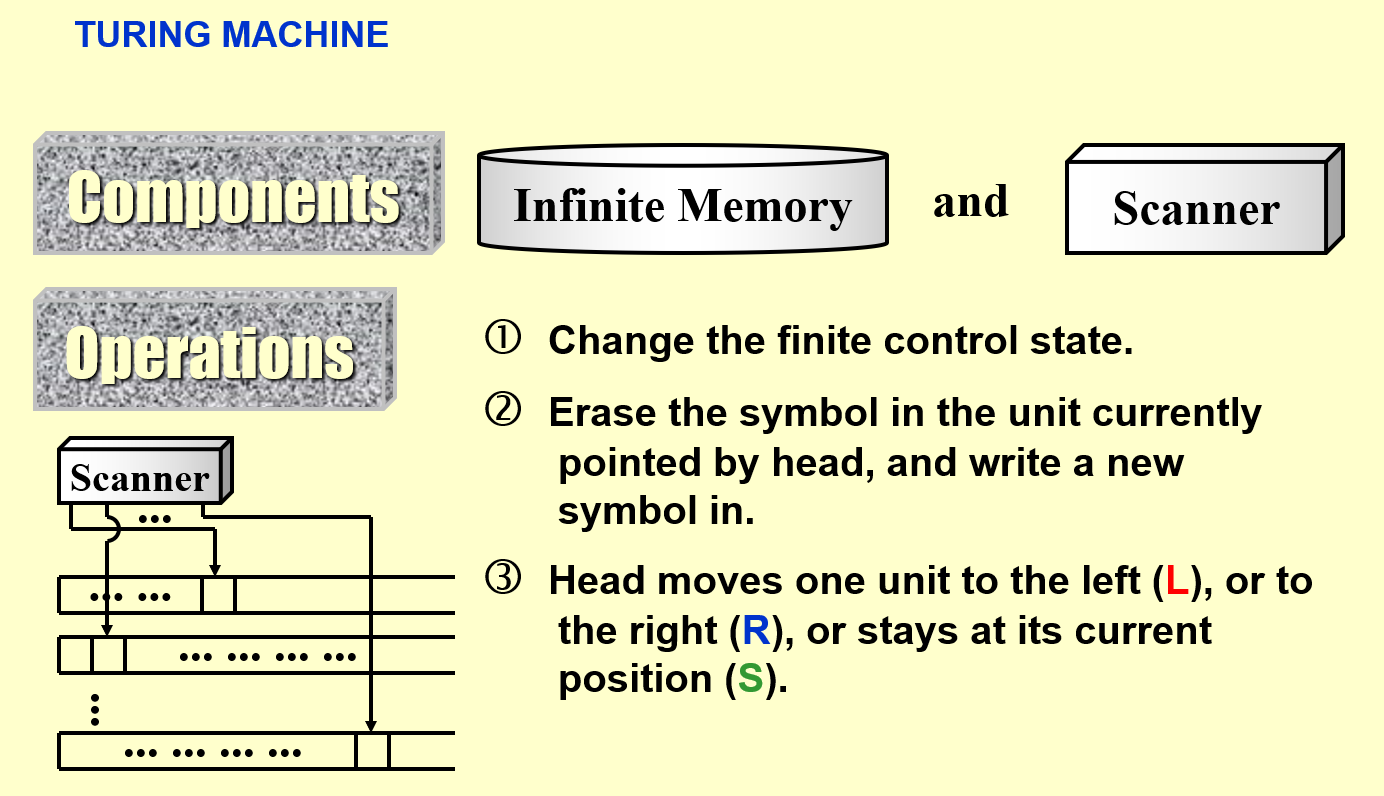
10.3.1 图灵机

图灵机由一个无限长的纸带和一个读写头组成。纸带被划分为一个个格子，每个格子上有一个符号，读写头可以在纸带上移动，读写头可以读取当前格子上的符号，也可以改变当前格子上的符号。图灵机的状态是一个有限集合，每个状态都有一个转移函数，转移函数的输入是当前状态和当前格子上的符号，输出是下一个状态、下一个格子上的符号和读写头的移动方向

A Deterministic Turing Machine executes one instruction at each point in time. Then depending on the instruction, it goes to the next unique instruction.

确定性图灵机在每个时间点执行一条指令。 然后根据指令，它进入下一个唯一的指令。

A Nondeterministic Turing Machine is free to choose its next step from a finite set. And if one of these steps leads to a solution, it will always choose the correct one.

非确定性图灵机可以从有限集合中自由选择下一步。 如果这些步骤之一导致解决方案，它将始终选择正确的解决方案。

两者之间存在复杂度存在差异。假设两者都需要使用n步解决问题，其中非确定性图灵机在每一步都有k中选择，它需要在k种选择中找到正确的动作，所以需要遍历k种选择。那么确定性图灵机的时间复杂度是O(n), 非确定性图灵机的时间复杂度是O(k^n)。

两个图灵机在解决问题上没有差异，一个图灵机能够解决，那么另一个也能解决问题，无非是不同时间复杂度上的解决问题

10.3.2 P & NP

P 取自 polynomial time，指的是可以用[确定型图灵机（Deterministic Turing Machine）🔍]在多项式时间内解决的问题。

也就是我们通常意义下所说的，可以在多项式时间内解决的问题。

NP 即 nondeterministic polynomial time（非确定性多项式时间！=非多项式时间），指的是可以用[非确定型图灵机（Nondeterministic Turing Machine）🔍]在多项式时间内解决的问题。这个说法等价于可以用[确定型图灵机🔍]在多项式时间内验证（判断答案是否正确）。

也就是我们通常意义下所说的，可以在多项式时间内验证的问题。

The problem is NP if we can prove any solution is true in polynomial time.

example：Hamilton cycle problem：找到一个包含所有顶点的单个循环

• 当前没有找到在多项式时间内解决问题的解法
• 但是假设我们已知解法，显然可以在多项式时间内验证（把每一步走一遍），所以这是NP问题

看清题目，哈密顿回路问题（决策版）是可判定问题，但不是NP问题，是NPC问题

哈密顿问题（非决策，路径版）是一个NP问题，给定路径能在多项式时间内进行验证

P与NP之间的关系是\(P \subseteq NP\),也就是所有能在多项式时间内解决的问题，都属于NP问题，但是问题出在两者是否是真子集的关系？

同时并非所有可判定的问题都在 NP 中。 例如，考虑确定图是否没有哈密顿循环的问题。假如给你一个解法，你要么利用该解法找到哈密顿回路，要么就是遍历所有的回路，说明所有的回路都不是哈密顿回路

10.4 NPC 问题

An NP-complete problem has the property that any problem in NP can be polynomially reduced to it.

所有的NP问题，都能够多项式归约到NPC问题，但是NPC不能归约到NP问题

If we can solve any NP-complete problem in polynomial time, then we will be able to solve, in polynomial time, all the problems in NP!

如果我们能在多项式时间内求解任何NP完全问题，那么我们将能够在多项式时间内求解NP中的所有问题！

10.4.1 多项式时间归约

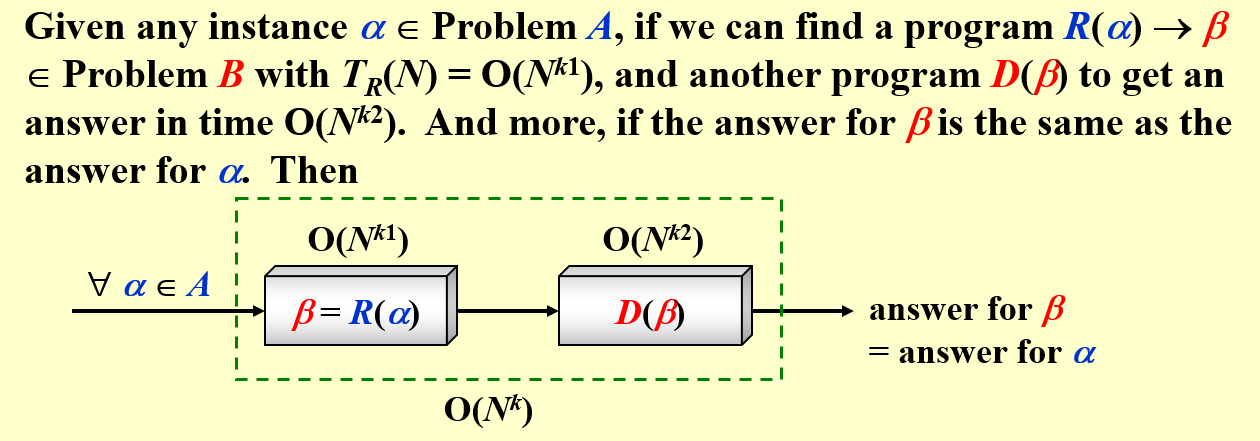
我们引入 P/NP 等这些概念，是为了衡量问题的复杂程度，而如何在具体的“问题”间传递、比较这种“复杂程度”，就是多项式时间归约(polynomial reduce)的目的。

graph LR
问题A --多项式时间转化--> 问题B

如果我们能在多项式时间的复杂度内，将问题 A 转化为问题 B，则称问题 A 可以多项式时间归约(polynomial reduce)为 B，记为\(A \leq_{p} B\)，表示 A 不会比 B 难。

而采取数学语言来描述，则是：

\[ \begin{aligned} A \leq_{p} B \;\;\Leftrightarrow\;\; & \exist f() \text{ which runs in polynomial time}, \\ & s.t. \;\; \forall x \in A,\; f(x) \in B \\ & \text{and}\; \forall f(x) \in B,\; y \in A \end{aligned} \]

将问题A多项式规约到问题B，则问题A不会比问题B难。

也就是说问题的难度小于问题B，也就是说我们总是将一个简单的问题归约转化为一个较难的问题

• 如果问题B是P问题，那么问题A也是P问题，两者都能用多项式时间进行解决
• 如果A是一个NP问题，那么B也是一个NP问题

if\(L_1 \leq_p L_2\),说明问题L1在多项式时间复杂度内是可以归约到\(L2\)的。也就是说，L2如果是P（多项式可解的），那么L1也是P问题（多项式可解的）。

L2如果是NP问题（多项式可验证），那么要验证L1的一个解是否正确，就要先用多项式时间将L1的这个解转化为L2的一个解，然后再用多项式时间验证L2的这个解是否正确，因此L1也是NP问题

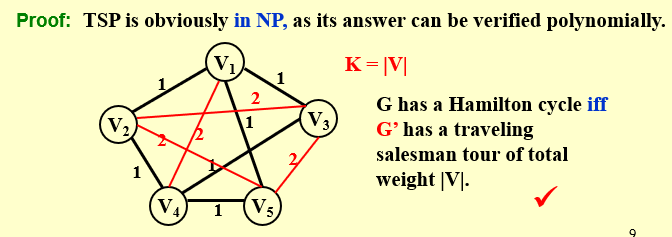
example：假设我们已知 Hamilton Cycle Problem 问题是一个 NPC 问题，尝试通过多项式时间归约🔍的方式来证明 TSP 也是一个 NPC 问题。

Suppose that we already know that the Hamiltonian cycle problem is NP-complete. Prove that the traveling salesman problem is NP-complete as well.

• Hamiltonian cycle problem: Given a graph\(G=(V, E)\), is there a simple cycle that visits all vertices?

• Traveling salesman problem: Given a complete graph\(G=(V, E),\)with edge costs, and an integer K, is there a simple cycle that visits all vertices and has total cost\(<=\)K?

目标：将哈密顿回路问题归约到旅行者问题（NPC->???）

对比 HCP 和 TSP 的差异。

以 HCP 为基础描述 TSP，实际上就是在一张完全图上寻找总长不超过\(k\)的哈密顿环路，具体来说：

HCP	TSP
图\(G(V,E)\)	完全图\(G'(V',E')\)
无边权	有边权
-	\(\sum v_i \leq k\)

1. 先证明TSP问题是NP问题：显然只需要验证给定的答案能够满足条件即可，重新走一遍就好了,只需要\(𝑂(𝑁)\)的开销就能验证
2. 由于TSP问题要求是完全图，也就是每两点之间都有一条边，我们现在哈密顿问题的基础上补全图，将没有连的边都连起来，权重标为2，原先已经在的权重就标为1，得到的新图标记为\(G'\)
3. 那么问题就转化为：\(G\)有哈密顿回路当且仅当\(G'\)满足TSP问题，且\(K = |V|\)
4. 所以如果哈密顿回路问题是NPC问题，那么TSP也是一个NPC问题(原问题为在\(G\)上寻找哈密顿环，等价于在\(G' = f(G)\)上做\(K = |V|\)的 TSP。由此证明\(\text{HCP} \leq_{p} \text{TSP}\))

旅行商问题TSP存在两种定义：

1. 给定一个完全图，判断是否存在一条路径，使得它经过图中的每个点恰好一次，且最后回到起点，且路径长度最短。

   该版本的 TSP 问题是一个 NPH 问题，常常出现在组合优化的语境中

2. 给定一个完全图，判断是否存在一条路径，使得它经过图中的每个点恰好一次，且最后回到起点，且路径长度不超过\(k\)。

   该版本的 TSP 问题是一个 NPC 问题，常常出现在复杂度理论的语境中。

10.5 形式化语言

10.5.1 Abstract Problem

an abstract problem Q is a binary relation on a set I of problem instances and a set S of problem solutions.

抽象问题 Q 是一组问题实例和一组问题解 S 上的二元关系。

example:

• For SHORTEST-PATH problem

\(I = { <G, u, v>: G=(V, E) \ is \ an \ undirected \ graph; u, v \in V };\) \(S = { <u, w_1, w_2, …, w_k, v>: <u, w_1>, …, <w_k, v> \in E }.\)

\(For \ every \ i \in I\),\(SHORTEST-PATH(i) = s \in S.\)

• For decision problem PATH:

\(I = { <G, u, v, k>: G=(V, E) \ is \ an \ undirected \ graph; u, v \in V; k ≥ 0 \ is \ an \ integer };\)

\(S = { 0, 1 }.\) \(For\ every \ i \in I, PATH(i) = 1 \ or \ 0.\)

如果两个形式化语言表示问题都是P问题，那么它们的交集、闭包都能在多项式时间内完成，还是P问题。也就是说P问题具有封闭性

那如果是NP问题呢？

如果\(A(x) = 1\)，则算法 A 接受字符串\(x ∈ {0， 1}\)

如果\(A(x) = 0\)，则算法 A 拒绝字符串 x

如果 L 中的每个二进制字符串都被 A 接受，并且 L 中的每个二进制字符串都被 A 拒绝，则算法 L 由算法 A 决定

要接受一种语言，算法只需要担心 L 中的字符串，但要决定一种语言，它必须正确接受或拒绝\({0， 1}\)中的每个字符串

验证算法是双参数算法 A，其中一个参数是普通输入字符串 x，另一个参数是称为证书的二进制字符串 y。

如果存在证书 y，则双参数算法 A 验证输入字符串 x，使得\(A（x， y） = 1。\)

验证算法 A 验证的语言是\(L = { x ∈ {0， 1} ： 存在 y ∈ {0， 1}，使得 A(x， y) = 1}。\)

刚刚我们研究得到P问题的补集也属于P问题

现在我们研究NP的问题的补集是否也是NP问题？

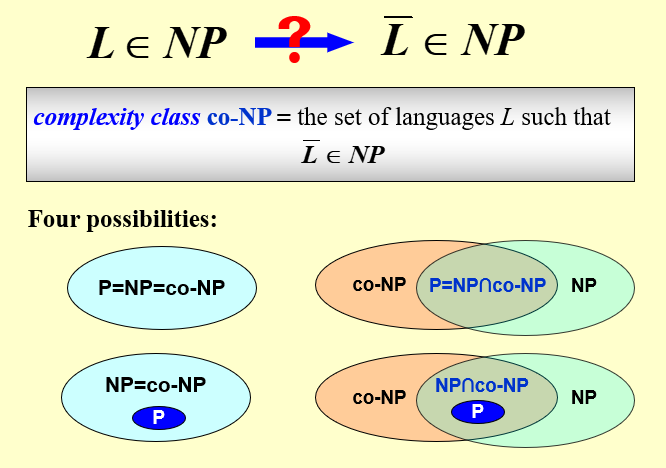
定义co-NP的条件为\(L\)的补集\(\overline L \in NP\)，一共存在以下四种可能

根据co-NP和P的定义，你会发现，\(P \in NP\)并且\(P \in\)\(co-NP\)

因为如果\(L \in P\), 那么\(\overline L \in P \subseteq NP\)符合co-NP的条件

-\(NP = co-NP\)

1. 若$P = NP$,根据$P$的**封闭性**可得$L \in P \Leftrightarrow \overline L \in P$,又因为co-NP条件为$\overline L \in NP$,所以$P=NP=$co-NP

2.$NP = co-NP, P \in NP, P\in co-NP$

-\(NP != co-NP\)

1.$P \in NP \cap co-NP$

2.$P = NP \cap co-NP$

形式化语言的归约

A language\(L1\)is polynomial-time reducible to a language\(L2\)(\(L1 ≤_p L2\)) if there exists a polynomial-time computable function\(f : \{0, 1\} → \{0,1\}\)such that for all\(x \{0, 1\}, x \in L1 \ iff \ f (x) \in L2.\)

We call the function\(f\)the reduction function(归约函数), and a polynomial-time algorithm\(F\)that computes \(f\)is called a reduction algorithm（归约算法）.

A language L ⊆ {0, 1}* is NP-complete if

1. L ∈ NP, and
2. \(L' ≤_p L \ for \ every L’ ∈ NP.\)

例子：将顶点覆盖问题归约到clique problem（分团问题）

假设我们已经知道分团问题（clique problem）是NP完备的。 证明顶点覆盖问题也是 NP 完备的。

• Clique problem: Given an undirected graph\(G = (V, E)\)and an integer\(K\), does\(G\)contain a complete subgraph (clique) of (at least)\(K\)vertices?

CLIQUE = { <G, K> : G is a graph with a clique of size K }.

• Vertex cover problem: Given an undirected graph\(G = (V, E)\)and an integer\(K\), does\(G\)contain a subset\(V' \subset V\)such that\(|V'|\)is (at most)\(K\)and every edge in\(G\)has a vertex in\(V'\)(vertex cover)?

VERTEX-COVER = { <G, K> : G has a vertex cover of size K }.

证明：

1. VERTEX-COVER ∈ NP

   Given any\(x = <G, K>\), take\(V' \subseteq V\)as the certificate\(y.\) Verification algorithm: check if\(|V'| = K\); check if for each edge\((u, v) ∈ E\), that\(u ∈ V'\)or\(v ∈ V'\).

   时间复杂度为：每条边检测是否有顶点位于V‘中，一共有N条边\(O(N \times N \times N = N^3)\)

2. CLIQUE\(≤_p\)VERTEX-COVER (证明分团问题 no harder than顶点覆盖问题)

   G has a clique of size K iff\(\overline G\)has a vertex cover of size\(|V| - K\).

   \(\Rightarrow\)

   • \(G\)中存在分团子集\(V' \subseteq V\)其大小为\(|V'| = K\)，令边\((u,v)\)表示不在\(E\)中的边，也就是根据\(V\)将原图补全成完全图的边
   • 那么肯定存在一个点\(u/v\)不在\(V'\)中，也就是说存在于\(V - V'\),此时刚好说明\(\overline G\)(原图的补图)中每一条边都至少有一个顶点存在于\(V - V'\)中
   • 刚好满足顶盖覆盖的定义，所以\(\overline G\)has a vertex cover of size\(|V| - K\).

   \(\Leftarrow\)

   • 已知补图满足顶点覆盖，对任意的边\((u,v) \notin E\),\(u \in V'\)或者\(v \in V'\)
   • 那么对于同时不在\(V’\)的点构成的边\((u,v) \in E\),所以\(V-V'\)is a clique and it has size\(|V|-|V'| = K.\)

10.6 习题集

1. If\(𝐿1≤_p𝐿2\)and\(𝐿2∈𝑁𝑃\), then\(𝐿1∈𝑁𝑃\). (T/F)

   T,这里的\(≤_p\)表示no harder than， 其实是\(L_1\)可以多项式归约至\(L_2\),由于\(L_2 \in NP\),那么\(L_2\)可以在非确定性图灵机上在多项式时间范围内解决问题，所以\(L_1\)也能够在非确定性图灵机上多项式时间解决

2. All NP-complete problems are NP problems.

   T,所有的NPC问题都是NP问题.NPC = NP\(\cap\)NPH

3. All the languages can be decided by a non-deterministic machine.

   F,忽略了不可判定问题。非确定性图灵机能够处理NP问题，确定性图灵机能够处理P问题.NPH问题无法使用不确定性图灵机进行验证

4. If a problem can be solved by dynamic programming, it must be solved in polynomial time.

   F,背包问题，但是不能用多项式时间进行解决，原因是输入的数据不是多项式的

5. all decidable problems are NP problems.

   F,但并非所有的decidable problems都可以在多项式时间内验证解，还包括NPH问题

6. Among the following problems, __ is NOT an NP-complete problem.

   A.Vertex cover problem

   B.Hamiltonian cycle problem

   C.Halting problem

   D.Satisfiability problem

   C是不可判定问题，顶点覆盖问题和分团问题（clique problem），哈密顿回路问题和旅行商问题。D选项是最早发现的NPC问题

7. Suppose\(𝑄\)is a problem in\(𝑁𝑃\), but not necessarily NP-complete. Which of the following is FALSE?

   A. A polynomial-time algorithm for SAT would sufficiently imply a polynomial-time algorithm for\(𝑄\).

   B. A polynomial-time algorithm for$𝑄$would sufficiently imply a polynomial-time algorithm for SAT.

   C. If\(Q \notin P\), then 𝑃≠𝑁𝑃.

   D. If 𝑄 is NP-hard, then 𝑄 is NP-complete.

8. 

9.