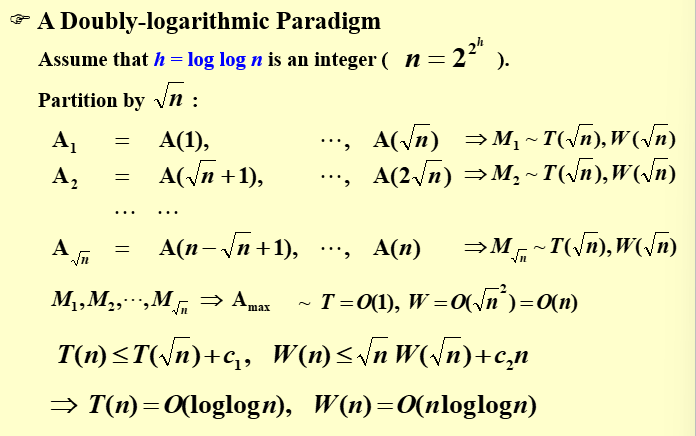跳转至

14. Parallel Algorithm

约 3855 个字 17 行代码 预计阅读时间 19 分钟

  1. 指令级并行（Instruction-Level Parallelism，ILP）：在一个CPU 内部，多条指令可以同时执行；例如大家现在就已经学过的流水线CPU，以及将来可能会学到的乱序、多发射以及超长指令字（VLIW，即把不相关的指令封装到一条超长的指令字中、超标量（例如有多个ALU，可以同时运行没有相关性的多条指令）等；

  2. 数据级并行（Data-Level Parallelism，DLP）：即将相同的操作同时应用于一些数据项的编程模型，例如经典的SIMD（Single Instruction, Multiple Data）架构，即一条指令同时作用于多个数据，例如用一条指令实现向量加法，两个向量中每对对应的元素相加互不干扰，所以可以同时进行所有的加法；

  3. 线程级并行（Thread-Level Parallelism，TLP）：一种显式并行，程序员要设计并行算法，写多线程程序，这也是本讲将要讨论的内容。线程级并行主要指同时多线程（SMT，是一种指令级并行的基础上的扩展，可以在一个核上运行多个线程，多个线程共享执行单元，以便提高部件的利用率，提高吞吐量）/超线程（HT，一个物理CPU 核心被伪装成两个以上的逻辑CPU 核心，看起来就像多个CPU 在同时执行任务，是通过在一个物理核心中创建多个线程实现的）以及多核和多处理器。

14.1 并行算法基本模型

定义 加速比（Speedup）是指在并行计算中，使用p 个处理器时相对于使用一个处理器时的性能提升比例，即 $$ S(p) = \dfrac{T_1}{T_p} $$ 其中\(T1\)是使用一个处理器时的运行时间，\(Tp\)是使用\(p\)个处理器时的运行时间。

显然最理想的情况下，加速比应当是p，即使用p 个处理器时的运行时间是使用一个处理器时的1/p。然而实际情况中，由于并行算法的设计和实现都有一定的困难：

  • 首先，使用多个处理器意味着额外的通信开销；
  • 其次，如果处理器并未分配到完全相同的工作量，则会产生一部分的闲置，就会造成负载不均衡（load unbalance），再次降低实际速度；
  • 最后，代码运行可能依赖其原有顺序，不能完全并行。

上述矩阵相乘并行算法可能有很多个CPU 同时访问了原始矩阵的同一个元素，比如同时得到C 的第一行的所有元素需要同时访问A 的第一行的所有元素。事实上，这种算法模型被称为PRAM 模型（Parallel Random Access Machine），是RAM 模型（Random Access Machine）在共享内存系统上的扩展。该模型假设所有处理器共享一个连续的内存空间。此外，模型还允许同一位置上同时进行多个访问。这在实际应用中，特别是在扩大问题规模和处理器数量的情况下是不可能的。对PRAM 模型的另一个反对意见是，即使在单个处理器上，它也忽略了内存的层次结构（即忽略了cache 等）。但在我们接下来的理论讨论中，我们忽略这些问题，因为我们的目的是讨论并行算法的基本思想。我们使用PRAM 模型，这一模型有规定如下三种内存共享方式：

  1. EREW（Exclusive Read Exclusive Write）：每个内存位置在任意时刻只能被一个处理器读取或写入；
  2. CREW（Concurrent Read Exclusive Write）：每个内存位置在任意时刻可以被多个处理器读取，但只能被一个处理器写入；
  3. CRCW（Concurrent Read Concurrent Write）：每个内存位置在任意时刻可以被多个处理器读取或写入，因为写入涉及到同时写入不同值可能造成的冲突，因此写入策略又可以分为如下三种：

(a) CRCW-C（Common）：所有处理器写入的值相同时才会写入； (b) CRCW-A（Arbitrary）：所有处理器写入的值可以不同，任意选取其中一个写入即可； (c)CRCW-P（Priority）：所有处理器写入的值可以不同，但是有一个优先级，只有优先级最高的写入才会生效。

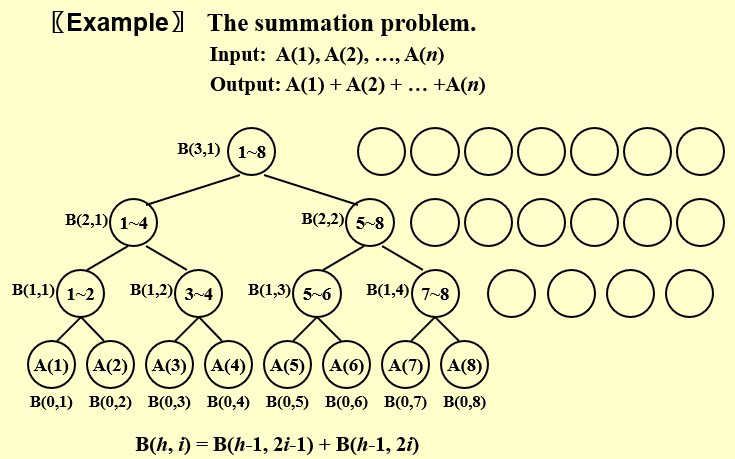
14.2 The Summation Problem

image-20240527102310349

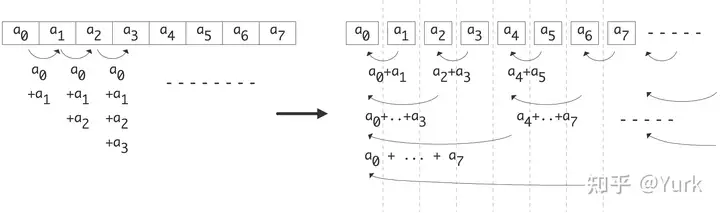
 for (s=2; s<2*n; s*=2)
      for (i=0; i<n-s/2; i+=s)
        x[i] += x[i+s/2]

img

image-20240527102615828

随着h的增加，需要使用的处理器的数量逐渐减少。但是又为每一个processor分配了任务（stay idle），这是不必要的

改进

image-20240527103209122

pardo表示不指定运行的processor，由编译器自行决定任务的分配。使用的寄存器的数量也随之减少

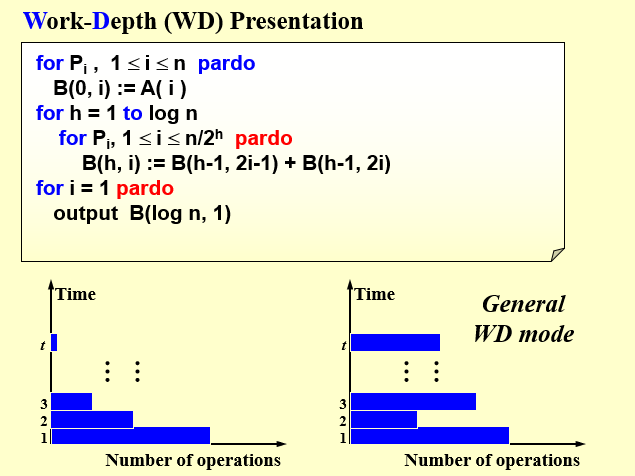
Measuring the performance

  • Work load – total number of operations: W(n)

  • Worst-case running time: T(n)

  • W(n) operations and T(n) time
  • P(n) = W(n)/T(n) processors and T(n) time (on a PRAM)
  • W(n)/p time using any number of p ≤ W(n)/T(n) processors (on a PRAM)
  • W(n)/p + T(n) time using any number of p processors (on a PRAM)

计算n个数的和问题中，时间复杂度是O(log N),如果给定的处理器数量为n/2，会使得最底层的运算次数加一，于是T'(n) = T(n) + 1

定理：设一个并行计算问题的工作量为W，关键路径长度为D，那么使用p个处理器的并行时间具有如下上下界： $$ \dfrac{W}{p} \leq T_p \leq \dfrac{W-D}{p} + D $$ 下界是显然的，受到理想加速比的限制

对于上界，因为关键路径的长度为D，算法的执行可以分为D个内部并行，互相之间串行的阶段，每一个阶段的工作量为\(W_i\),\(W = \underset{i = 1}{\sum}W_i\)

使用p 个处理器时，每一个阶段所需的时间为dWi/pe，向上取整的原因在于，每个阶段的工作量可能不能被p 整除，比如大任务被分成了7 个子任务，7 个任务分配给3 个处理器，那么每个处理器分配到的任务数应当是2，2，3。

需要的总时间为： $$ T_p = \sum_{i=1}^D \lceil \dfrac{W_i}{p}\rceil= \sum_{i=1}^D \lceil \dfrac{W_i - 1}{p}\rceil + 1 \leq \sum_{i=1}^D \dfrac{W_i - 1}{p} + 1 =\dfrac{W-D}{p}+D $$

临界状态，处理器的数目变为n/log n

image-20240527104620123

矩阵乘法：两个n阶方阵A和B相乘得到矩阵C，显然总的操作数是2\(n^3\)(乘法和加法)，如果我们有\(n^2\)个处理器，可以让每一个处理器负责结果矩阵C的一个元素的计算。这样并行计算需要的时间就是计算一个元素的时间，也就是\(2n\)

现在提供更多的处理器，用于加速n个对应元素乘法的和，利用上面提到的算法，额外提供n/2个处理器，加法的时间复杂度会从O(n)下降到O(logN)

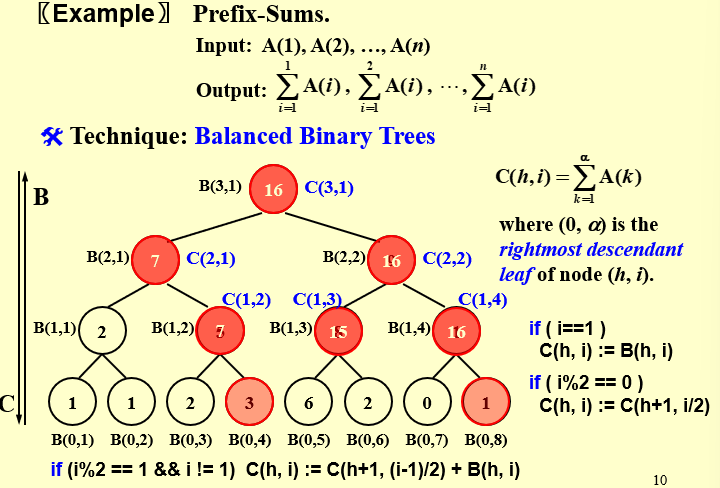
14.3 Prefix-Sums

image-20240527110214946

我们可以从上往下计算这个C，每一层计算都可以并行，直到算完C(0, i) 实际上就是1 到i 的前缀和。因此关键就是怎么从上往下计算，并且保证每一层都能并行

B(h,i)记录的是summation problem记录的值，与前缀和问题存在着重合之处

C(h,i)表示前2^h * i个点的和

  • 如果i=1，那么C(h,i) = B(h,i).因为i=1时，根据定义，C(h,i)等于从第一个元素开始加到该点为根结点的右子树的右下角叶子。所以两者相等
  • 如果i是偶数，这表明这一点是某个点的右儿子，因此它和它的父亲的最右下角的叶子是同一个，因此有C(h,i) = C(h+1,i/2)
  • 如果i是奇数且不是1，这表明该点是某一个点的左儿子，首先它自己的值B(h, i) 不是从1 开始加的，所以我们要选一个左边的点，把从1开始加到这个点对应的之前的部分补上。所以C(h,i) = C(h+1,(i-1)/2) + B(h,i).

image-20240527110234942

显然这一并行算法的深度是O(log n)，总工作量是O(n)，因为无非就是在完全二叉树上先从下往上，然后再从上往下分层遍历了两轮。

14.4 Merge

image-20240527111556042

关键在于求出A元素在B中的排序或者B元素在A中的排序

image-20240527111701941

image-20240527111917893

Binary Search:在n个处理器的基础上，计算排序所需的时间复杂度为O(log n),如果是单个处理器，所需的时间复杂度为O(nlog n)

使用二分查找找到一个元素在另一个数组中的位置只需要O(logN)的时间，即深度D=O(logN),总工作量为O(nlogn),然后我们需要将元素放到正确的位置上，这一深度为O(1),总工作量为O(n),两步合在一起深度就是O(logn),总工作量为O(nlogn)

Serial Ranking:

两个数组的元素从头依次向后比较

Binary Search所需的时间更少，Serial Ranking所需的操作数量更小

改进：Parallel Ranking 使用划分范式的方法

image-20240527112958744

假设每一段的长度为log n，那么能够分成 n/log n段

先对每一段的段头进行排序

再只需要保证段头之间的结点是有序的，那么C就是有序的

  1. 划分：我们将数组划分为p份（此时p未知，需要经过分析选取到最优的p）。我们首先对每一个子问题的第一个元素求出它在另一个数组中的位置，使用二分查找而非线性搜索，深度为O(logn),总工作量为O(plogn)

  2. 真实工作：剩下的工作就是相邻两个箭头之间的部分需要在最终数组中确定相对位置。相邻的两个箭头的距离不会超过n/p，并且一个数组上有p个出发的位置和p 个到达的位置，所以在任意一个数组上，出发点和到达点一共最多有2p个。对应的还剩下2p个大小为O(n/p)的子问题。

如果采用线性查找，深度就是O(n/p),总工作量为2p*O(n/p) = O(n),如果采用二分查找，总工作量就是\(2p \times \frac{n}{p}O(log \frac{n}{p}) = 2n log \frac{n}{p}\)

  1. 接下来希望找到一个最优的p，使得第一步的总工作量为O(n),第二步的深度为O(log n),也就是集成之前Binary Search和serial Ranking的优点。于是得到\(p=n/logn\)

14.5 Maximum Finding

image-20240527113513059

第一种最简单的想法就是类似于前面求和问题的做法，构造一棵二叉树，初始元素两两分组比较，然后逐层上递，最终得到最大值。这样的算法深度为O(log n)，总工作量为O(n)。

第二种方法是并行比较每一对元素的值。只要A[i]<A[j],就往B[i]中写1，最后只有最大的数不会被写1。在并行比较每一对元素时，我们可能会有多个线程同时往数组B 中进行写入，实际上我们只需要使用前面提到的CRCW 策略允许同时写入，然后按common rule 写入即可，因为这里所有线程往任意一个B[i] 只会写入1 这个数字，所以写入的内容都是一样的。

最后得到深度为O(1),总工作量为O(n^2)

image-20240527114430453

双对数范式

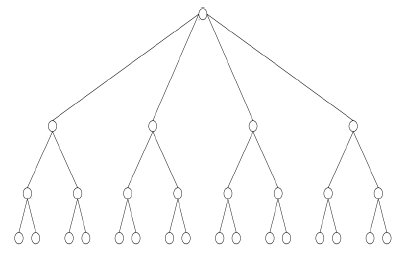
双对数范式是一种可以二叉树的扩展。在完全二叉树中，设叶子的数量为n，那么树高是log n 级别的，这里双对数则是希望构造一棵树，使得树高是log log n 级别的。为了构造这样一棵树，我们首先设树中每个节点的level 为从根到该节点的距离（需要经过的边数），根的level 为0。接下来我们构造这棵树如下：

  1. 设某个结点的level为s，当\(s \leq loglogn-1\)时，则它有\(2^{2^{h-s-1}}个孩子\)
  2. 当\(s = loglogn\)时，它有2个孩子作为树的叶子

image-20240530195027929

每一段的长度为\(\sqrt n\),一共有\(\sqrt n\)段

image-20240527114830853

把数据划分成更小段，每一段的长度为loglog n

  1. 将数组分为\(n/ log log n\)份，即每一份的大小为\(log log n\)，如PPT 第20 页；实际上每一份的大小都很小了，所以我们可以直接利用线性查找的方式找到每一份的最大值，则每一份的深度和工作量都是\(O(log log n)\)的；
  2. 然后我们对上面求出的\(n/ log log n\)个最大值使用双对数范式的算法。

image-20240527120646764

image-20240527120703385

14.6 习题集

  1. While comparing a serial algorithm with its parallel counterpart, we just concentrate on reducing the work load.

    F，除了work load还需要关注时间复杂度。分别对应W和T

  2. To evaluate the Prefix-Sums of a sequence of 16 numbers by the parallel algorithm with Balanced Binary Trees, C(4,1) is found before C(2,2).

    计算前缀和时，从上往下计算。对于summation问题，B[]是从下往上计算的

  3. To evaluate the sum of a sequence of 16 numbers by the parallel algorithm with Balanced Binary Trees, B(1,6) is found before B(2,1).

    B[]从下往上计算

  4. In order to solve the maximum finding problem by a parallel algorithm with\(T(n)=O(1)\), we need work load\(W(n)=Ω(n^2)\)in return.

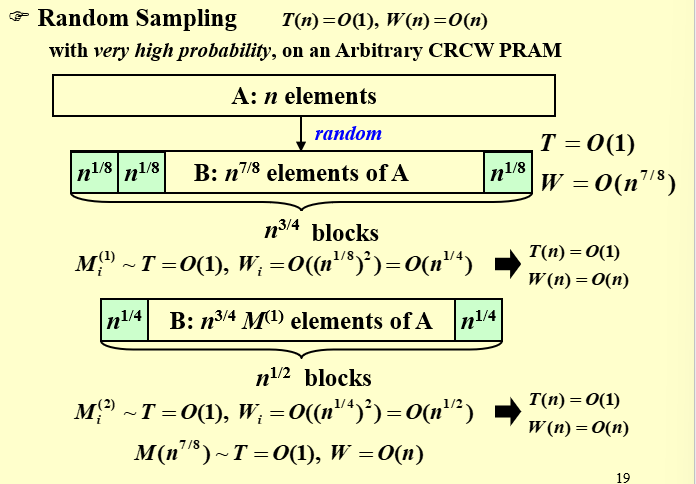
    F.采用 Random Sampling，就可以在$𝑊(𝑛)=𝑂(𝑛)$下得到结果。

  5. To solve the Maximum Finding problem with parallel Random Sampling method,\(O(n)\)processors are required to get\(T(n)=O(1)\)and\(W(n)=O(n)\)with very high probability

    T

  6. The prefix-min problem is to find for each i, 1≤i≤n, the smallest element among A(1), A(2), ⋯, A(i). What is the run time and work load for the following algorithm?

    for i, 1≤i≤n pardo
B(0, i) = A(i)
for h=1 to log(n)
for i, 1≤i≤n/2^h pardo
   B(h, i) = min {B(h-1, 2i-1), B(h-1, 2i)}
for h=log(n) to 0
for i even, 1≤i≤n/2^h pardo
   C(h, i) = C(h+1, i/2)
for i=1 pardo
   C(h, 1) = B(h, 1)
for i odd, 3≤i≤n/2^h pardo
   C(h, i) = min {C(h + 1, (i - 1)/2), B(h, i)}
for i, 1≤i≤n pardo
Output C(0, i)

    image-20240530200435587

    参照求前缀和问题，层数为logn,对应的时间复杂度是O(logn),每一个结点的值都需要计算，对应的也就是n+n/2+n/4+...+1 = 2n,work load就是O(n)

  7. Which one of the following statements about the Maximum Finding problem is true?

    A.There exists aserial algorithm with time complexity being\(O(logN)\).

    B.No parallel algorithmcan solve the problem in O(1) time.

    C.When partitioning the problem into sub-problems and solving them in parallel, compared with\(\sqrt N\), choosing\(loglogN\)as the size of each sub-problem can reduce the work load and the worst-case time complexity.

    D.Parallel random sampling algorithm can run in O(1) time and O(N) work with very high probability.

    D√

    关于C选项，partition by\(\sqrt N\),对应的时间复杂为\(T(N) = O(loglogN)\),对应的work load为\(O(NloglogN)\)

    partition by\(loglogN\),对应的时间复杂度为\(T(N) = loglogN\),对应的work load为\(O(N)\)

    所以时间复杂度不变，但是work load变小

  8. Sorting-by-merging is a classic serial algorithm. It can be translated directly into a reasonably efficient parallel algorithm. A recursive description follows.\(MERGE−SORT( A(1), A(2), ..., A(n); B(1), B(2), ..., B(n) )\)Assume that\(n=2^l\)for some integer\(l≥0\)

    if n = 1 then return B(1) := A(1)

    else call, in parallel,\(MERGE−SORT( A(1), ..., A(n/2); C(1), ..., C(n/2) )\)and

    • \(MERGE−SORT(A(n/2+1), ..., A(n); C(n/2+1), ..., C(n) )\)
    • \(Merge (C(1),...C(n/2)) \ and \ (C(n/2 + 1),...,C(n))\)into\((B(1), B(2), ..., B(n))\)with time O(n)

    Then the MERGE−SORT runs in __ .

    A.\(O(nlogn)\)work and\(O(log^2n)\)time

    B\(O(nlogn)\)work and \(O(logn)\)time

    C.\(O(nlog^2n)\)work and \(O(log^2n)\)time

    D.\(O(nlog^2n)\)) work and \(O(logn)\)time

    image-20240530201752836

  9. Which one of the following statements about the Ranking problem is true? (Assume that both arrays contain N elements.)

    A.There exists a serial algorithm with time complexity being\(O(logN)\).

    serial algorithm对应的时间复杂度和work load都是O(n)

    B.Parallel binary search algorithm can solve the problem in\(O(1)\)time.

    binary search对应的时间复杂度是O(logN)

    C.When partitioning the problem into sub-problems and solving them in parallel, choosing\(O(loglogN)\)as the size of each sub-problem can reduce the work load and the worst-case time complexity to\(O(logN)\).

    在Maximum Finding问题中，双对数范式分割，对应的时间复杂度是O(loglogN)

    D.There is a parallel algorithm that can run in\(O(logN)\)time and\(O(N)\)work.

    D选项，parallel ranking集成二分搜索的时间复杂度O(logN)和顺序查找的work load O(n)

image-20240530202139378