15. External Sorting¶

约 2765 个字 72 行代码预计阅读时间 15 分钟

15.1 外排序¶

普通的排序算法排序的对象都是放在内存里的一些数据，例如一个 int 数组。然而外部排序排序的对象，或者说要排序的那个“数组”，没法被完整地存在内存里，它们都被存储在硬盘之类的非易失介质中，而从这种介质里读取数据往往具有较大的开销，所以我们总是“一块一块”从里面那数据。

从执行的顺序来说，内排序中的归并排序是一个自上而下不断地划分，再自下而上不断归并的过程。相反，外排序由于其特性限制，其“归并段”并不是自上而下$\dfrac{1}{f}$划分出来的，而是根据硬件处理能力，直接划分好最小的归并段，然后直接自下而上归并。

而这样一个将 $𝑘⋅𝑐$ 个 run merge 成 $c$ 个 run 的过程，我们称之为一个 pass。（在归并树上体现为一层。）

15.2 example 2-way merge¶

如何减小pass的次数

Use a k-way merge!

数据最初保存在$T1$上，初始数组一共有$N$个元素，内存可以容纳（排序）$M$个元素。

从磁带$T1$读入$M$个记录，在内存中排序，将排好序的记录交替写入到$T2$和$T3$,每组排好序的记录叫做run（目前的长度为M）
接下来$T2,T3$作为输入磁带，$T1$的数据已经失效，和$T4$一起作为输出磁带。我们将$T2,T3$的第一个run取出，将两者合并，结果写入到$T1$,得到的是$2M$长度的run。我们再从磁带$T2,T3$取出下一个run，合并，将结果写入到$T4$。交替执行，直到$T2$或者$T3$为空，如果某一个磁带存在剩余元素，就直接拷贝到磁盘末尾。
重复相同的操作，结果得到长度为$4M$的run，重复直到得到长度为$N$的run
每执行一次合并，run的长度加倍，所以一共需要$\lceil log_2(N/M) \rceil$次合并（pass），外加上第一次构造初始的排好序的run，于是一共需要pass的次数是 $$ 1 + \lceil log_2(N/M) \rceil $$

例如PPT 上的例子，第一趟构造出长度为3 的run，接下来是三次pass（合并）：run长度依次由3 变6，6 变12，12 变13，因此共4 次pass。

15.3 k路合并¶

优化：采用多路合并

第一个优化的方向是减少工作的pass数量。如果我们使用k路的归并，也就是每一次归并k条磁带上对应位置的run，那么每一次合并之后，run的长度为增加k倍。

所以只需要

\[ 1 + \lceil log_k(N/M) \rceil \]

次pass，即可完成排序。减少了趟数，因此减少了磁带移动的次数，从而减少总时间。

k 路合并有一个实现上需要注意的点，因为我们是k 个run要合并，因此我们需要不断的在k 个元素中选取最小值放到输出的磁带上，这个操作可以使用优先队列来实现，PPT 第5 页给出了这样的例子。

此处增大k，使用三路归并，从划分好的最小归并段，从下往上合并

还需要T6用于存放最终的结果（最后的归并），所以需要2k个type。或者理解为，每一次都尽可能需要进行k路合并，那么显然需要k路的输入，因为输入和输出磁带的交替，所以输出磁带也需要k路，所以一共需要2k个磁带

15.4 多相合并（斐波那契）¶

k 路合并需要的磁带数目是2k，因为我们每次pass需要k 个输入磁带和k 个输出磁带。因此，如果k 很大，那么磁带数目就会很多，这是不太合理的。因此我们讨论另一种优化方案：多相合并，能够大大减小归并需要的磁带数目：k 路合并只需要k + 1 条磁带。

三条磁带，2路归并。T2和T3归并后结果保存在T1，下一次又要从T1将结果拷贝到T2和T3，拷贝需要的IO次数太多

先介绍均匀划分：
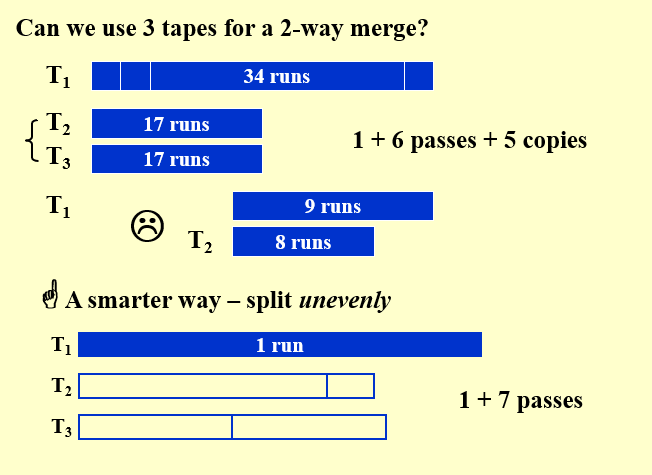
- 设有三盘磁带$T1$、$T2$ 和$T3$，在$T1$ 上有一个输入文件，它将产生34 个run。一种选择是在$T2 \(和$T3\) 的每一盘磁带中放入17 个run。然后我们可以将结果合并到T1 上，得到一盘有17 个run的磁带。
- 由于所有的run都在一盘磁带上，因此我们现在必须把其中的一些run放到T2 上以进行另一次的合并。执行合并的逻辑方式是将前8 个run从T1 拷贝到T2 并进行合并。这样的效果是，为了我们所做的每一趟合并，我们不得不附加额外的复制工作，而复制也需要磁头的移动，是很昂贵的操作，因此这种方法并不好。
- 如果我们接着把所有的步骤都画完，我们会发现我们总共需要1 趟初始+6 趟pass，外加5 次复制操作。
如果使用不均匀的划分，可以减少copy的次数，但是增加passes的次数
- 设我们把21 个run放到T2 上而把13 个run放到T3 上。然后，在T3 用完之前将13 个run合并到T1 上。然后我们可以将具有13 个run的T1 和8个run的T2 合并到T3 上。此时，我们合并8 个run直到T2 用完为止，这样，在T1 上将留下5 个顺串而在T3 上则有8 个run。然后，我们再合并T1 和T3，等等，直到合并结束

run的最初分配会影响排序的效率？那有该如何进行分配呢？

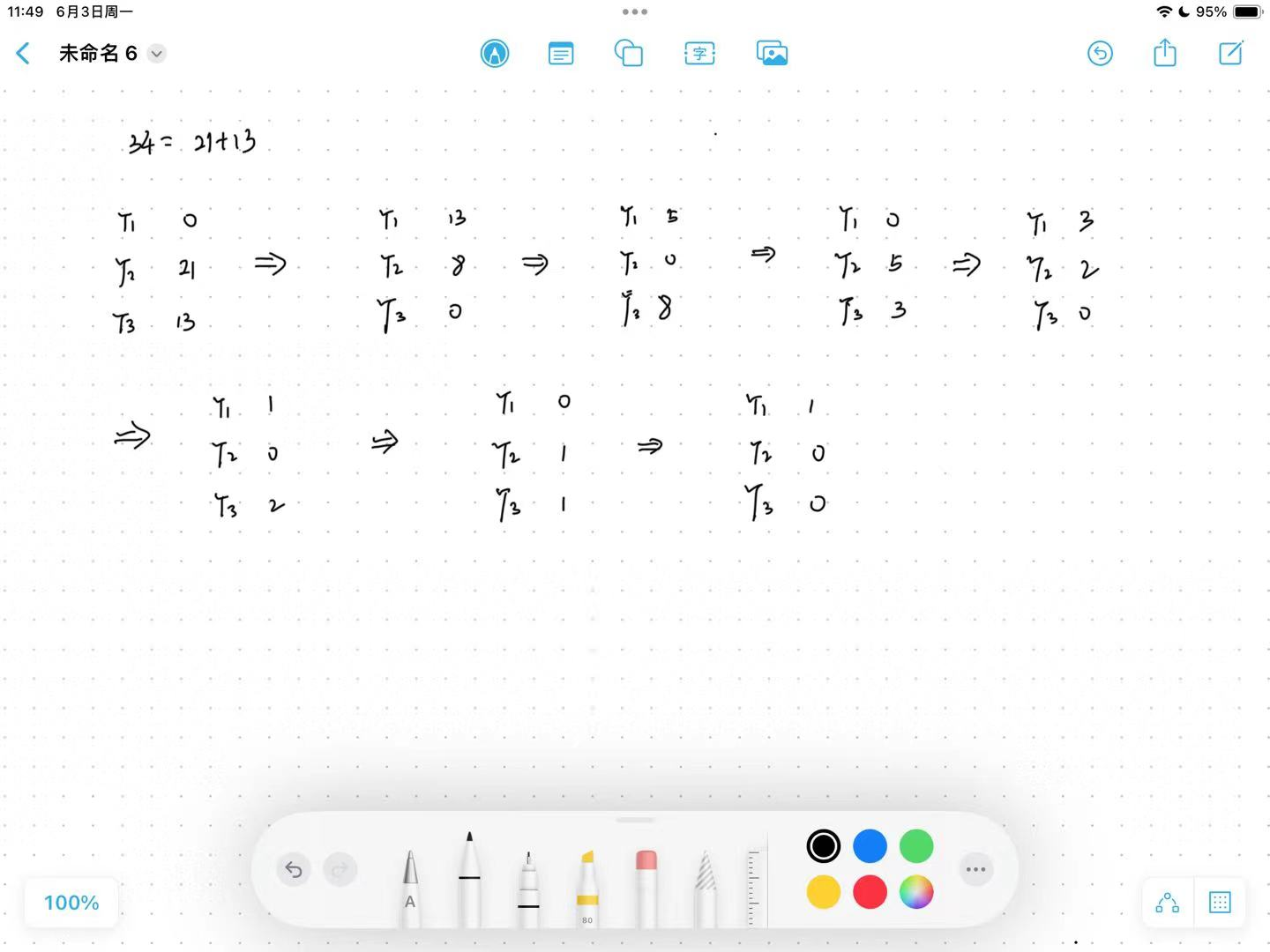
若22 个run放在T2 上，12 个在T3 上，则第一趟合并后我们得到T1 上的12 个run以及T2 上的10 个run。
在另一次合并后，T1 上有10 个run而T3 上有2 个run。此时，进展的速度慢了下来，因为在T3 用完之前我们只能合并两组run。这时T1 有8 个run而T2 有2 个run。同样，我们只能合并两组run，结果T1 有6 个run且T3 有2 个run。再经过三趟合并之后，T2 还有2 个run而其余磁带均已没有任何内容。我们必须将一个run拷贝到另外一盘磁带上，然后结束合并，所以非常复杂。

如何一个run的长度是斐波那契数$F_n$，那么分配这些run的最好的方式就是把它们分裂成两个斐波那契数$F_{n-1}, F_{n-2}$, 对于不是斐波那契数的run数，可以添加无穷大补成斐波那契数

现在扩充到k路合并，此时我们需要第k 阶斐波那契数用于分配run，其中k 阶斐波那契数定义为 $$ F^{(k)}(n) = F^{(k)}(n-1) + F^{(k)}(n-2) +...+ F^{(k)}(n-k) $$

15.5 缓存并行处理¶

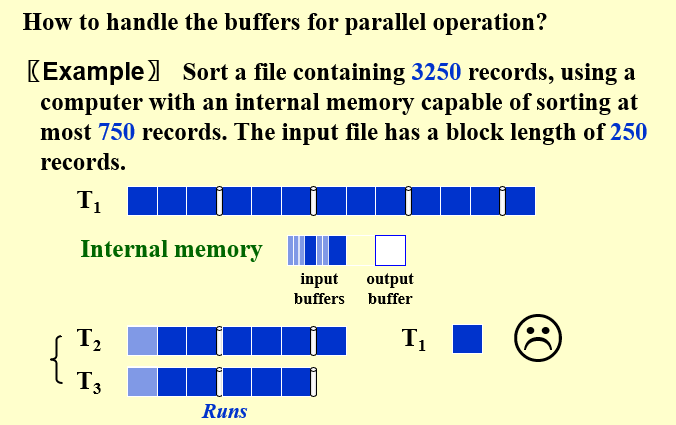
在实现外部排序的过程中，我们是一块一块地读入数据，但是并不是每比较一次就往磁盘中写入一个元素。所以我们是把内存划分为两个输入缓存区(buffer),一个输出缓存区，输入缓存区用来存放从输入磁盘读入的数据，然后两个输入缓存区的数据比较之后的排序结果先放到输出缓存区，当输出缓存区满了之后再一次性写入输出磁盘。

一次读2 * 250个record，结果暂存在输出缓冲区，直到数据积累到250，才写回到磁盘。能够减少IO次数

然而，这样的实现方式仍然存在问题。

当输出缓存区写回到磁盘时，内存里什么事情都干不了，影响排序效率。所以我们需要将输出缓存区也拆分成两个，当其中一个满了需要写回磁盘时，另外一个输出缓存区接收数据，也就实现了并行处理，一个在内存里操作，一个进行I/O交互

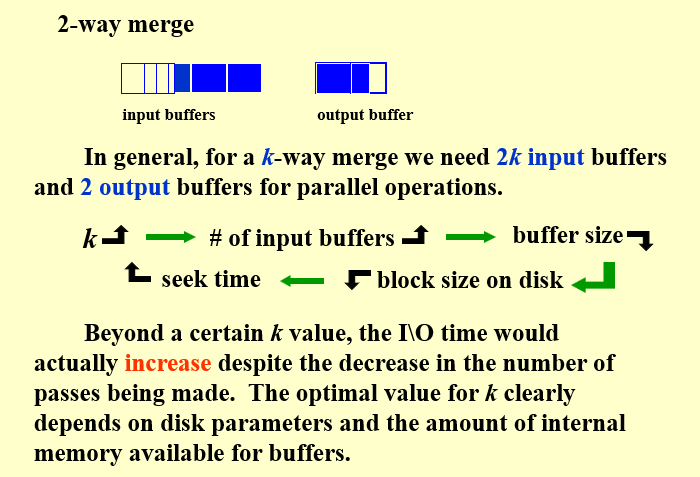
对于输入缓存区同理。如果仍然是2 个输入缓存，当所有输入缓存中的数据都比较完了，这时我们也要被迫停止等待新的数据从输入磁盘中读入。因此我们要进一步划分为4 个输入缓存，这样当其中两个输入缓存中的数据正在比较的时候，另外两个输入缓存可以同时并行地读入新的数据

这里解释为什么k太大时，k路合并尽管减少了pass的数量，但是并不一定更优的原因

这是因为：由于我们将内存区域，划分为2k个输入缓存区和2个输出缓存区，当k很大的时候，输入缓存就会划分的很细，一次能够读入到输入缓存的数据就会很少，block的大小降低，从而导致seek时间大大增多（I/O的次数增多）。尽管pass的次数减少，但是I/O操作次数增加，形成一个权衡。所以对于k存在一个最优值，根据实际进行选取

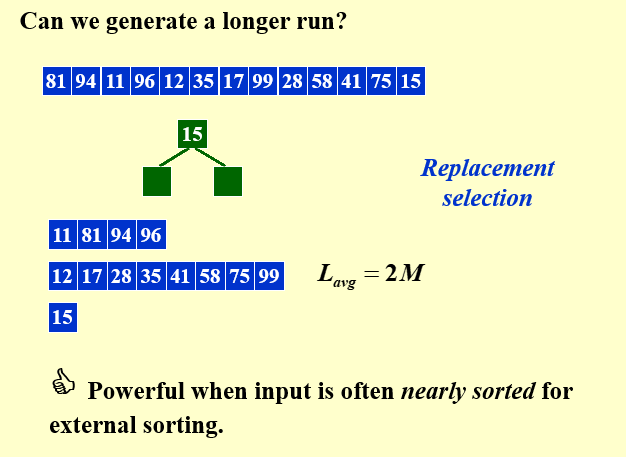
15.6 替换选择¶

迄今我们已经用到的策略是每个run的大小都是内存的大小，然而事实上这一长度还可以进一步扩展。

原因在于，我们某个内存位置中的元素一旦写入磁盘了，这个内存位置就可以空出来给数组后续的元素使用。只要后续的元素比现在写入的更大，就可以继续往run后面添加该元素。PPT 第10 页给出了很清晰的动态例子，我们在内存中维护一个优先队列，每次从队列中取出比当前run中最后一个元素更大的最小的元素写入磁盘，然后再从磁盘中读入一个元素放入队列中，直到队列中的元素都比run的最后一个要小，就开启一个新的run。

在平均情况下，替换选择生成的run的长度为2M，其中M时内存的大小。随着M的增大，意味着run的数量将会减少（N/2M），因此合并的pass次数也将减少，从而减少I/O操作的次数

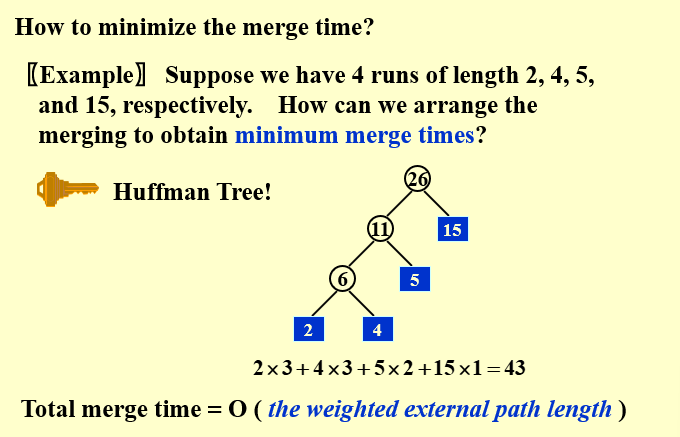
现在变成归并段有长有短，需要决定归并的次序

如何决定归并的次序？最优解是采用huffman树，让长的run尽可能少参与合并，那么显然贪心地不断选择最小的两个run进行合并是最优的。

#include<bits/stdc++.h>
using namespace std;

#define MAXSIZE 100000 + 5
int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    int temp[MAXSIZE];
    // ans[i]表示run的集合，i表示第i个run
    // temp1为first run，temp2为second run
    priority_queue<int, vector<int>, greater<int> > ans[100000], temp1, temp2;
    // ans的下标
    int index = 0; 
    for(int i = 0; i < n; i++)
    {
        scanf("%d", &temp[i]);
        if(i < m)
        {
            // 将前m个数放入first run中
            temp1.push(temp[i]);
            ans[index].push(temp[i]);
        }
        else
        {
            // 如果temp[i]比first run中的最小值大，满足当前集合的要求
            if(temp[i] > temp1.top())
            {
                // 删除first run中的最小值
                temp1.pop();
                // 将temp[i]放入first run中的末尾
                temp1.push(temp[i]);
                // 将temp[i]放入最终结果ans[cnt]
                ans[index].push(temp[i]);
            }
            else
            {
                // 否则， temp[i]比first run中的最小值还小，新建一个ans[cnt + 1]集合
                temp1.pop();
                // 将temp[i]放入second run中
                temp2.push(temp[i]);
                // 将temp[i]放入下一个集合中
                ans[index + 1].push(temp[i]);
            }

            // 如果first run为空，temp1中没有元素
            if(temp1.size() == 0 || i == n - 1 && temp2.size() != 0)
            {
                // 将second run中的元素放入first run中
                temp1 = temp2;
                // temp2清空
                temp2 = priority_queue<int, vector<int>, greater<int> >();
                // index++意味着到下一个run
                index++;
            }
        }

    }
    // 打印结果，每一行最后一个数后面没有空格
    for(int i = 0; i <= index ; i++)
    {
        if(ans[i].size() > 1)
        {
            while(ans[i].size() > 1)
            {
                printf("%d ", ans[i].top());
                ans[i].pop();
            }
        }
        printf("%d\n", ans[i].top());
    }
}