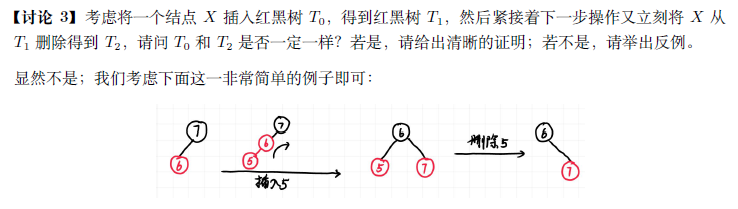
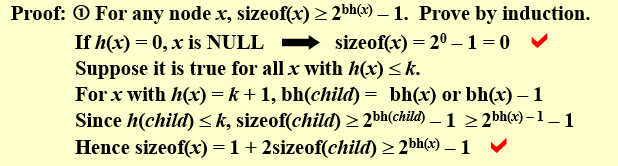2. Red Black Tree & B+ Tree¶
约 3363 个字 预计阅读时间 17 分钟
2.1 Red Black Tree¶
红黑树是满足如下性质的一种二叉搜索树:
-
Every node is either red or black.
-
The root is black.
-
Every leaf (
NIL) is black. -
if a node is red, then both its children are black.
-
For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
对于每个结点,从该结点到后代叶子的所有简单路径都包含相同数量的黑色结点。
注意点:
1. 红结点的父结点一定为黑结点
2. 性质3,所有的NULL leaf 都是black,你看到的leaf不是NULL,但是它的左右结点是NULL,未显示的左右儿子也是黑结点。此处叶子结点被重新定义,称所有两个子结点都是NULL的结点为末端结点(也就是传统意义上的leaf)
3. 由性质5得,合法红黑树的红色结点的两个子结点(存在且为黑色)一定都是叶子或者都不是叶子,不然从红结点出发,到两个子结点,包含不同数量的黑色结点
4. 我们称NIL 为外部结点(external),其余有键值的结点为内部结点(internal)。
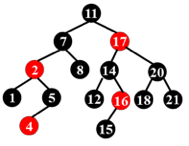
上图的红黑树是否合法?
16 号结点的右儿子是一个黑叶子(NULL),而这个叶子到根的路径上只有 3 个黑结点,而其他叶子到根都有 4 个黑结点。
black height的定义:特定结点的黑高,等于该结点到叶结点(NIL)到简单路径中(不包括自身),黑色结点的数量。记作\(bh(X)\),其中整棵红黑树的黑高也就是根结点的黑高
【lemma】一个有 \(N\) 个内部结点(不包括叶子结点)的红黑树,其高度最大为 \(2log_2(N + 1)\)。
【lemma】\(bh(Tree) >= h(Tree)/2\) 黑结点的数量至少占树高的一半
- 红黑树结点最少情况,全是黑结点,此时就是二分搜索树,二分搜索树\(sizeof(x) = 2^{h(x)} - 1\)。
请注意此处为内部结点大于是因为此时的二分搜索树并不一定是完全平衡二叉树 - \(bh(child) = bh(x)\ or \ bh(x)-1\), 分别对应child是否为黑结点
- \(sizeof(x) = 1 + 2 \times sizeof(child) >= 1 + 2 \times (2^{bh(child)}-1) >= 2 \times 2^{bh(x)-1} -1 = 2^{bh(x)}-1\)
- 红结点的孩子一定是黑结点,所以有红必有黑,任何路径上黑色结点必定占到至少一半的数量
2.1.1 Insert¶
前情提要:如果插入一个红色结点,也就是一个NULL结点被红色结点替代,此时并不会改变黑高。但是需要满足红色结点互不相邻的性质。
如果插入的是黑色结点,那么性质5一定会被打破,黑高一定会加1
总体思路为:先将红黑树当作普通的二叉搜索树,将目标数据插入到书中的末端,
并将它染成红色,再调整使之在满足黑高不变的情况下,红色结点不相邻
不妨先假设我们插入的是红色结点。
-
如果插在黑色结点下面,没有影响
-
如果插入空树,则将红结点直接变为黑结点
-
如果插入到红色结点的下面,此时破坏了性质4
-
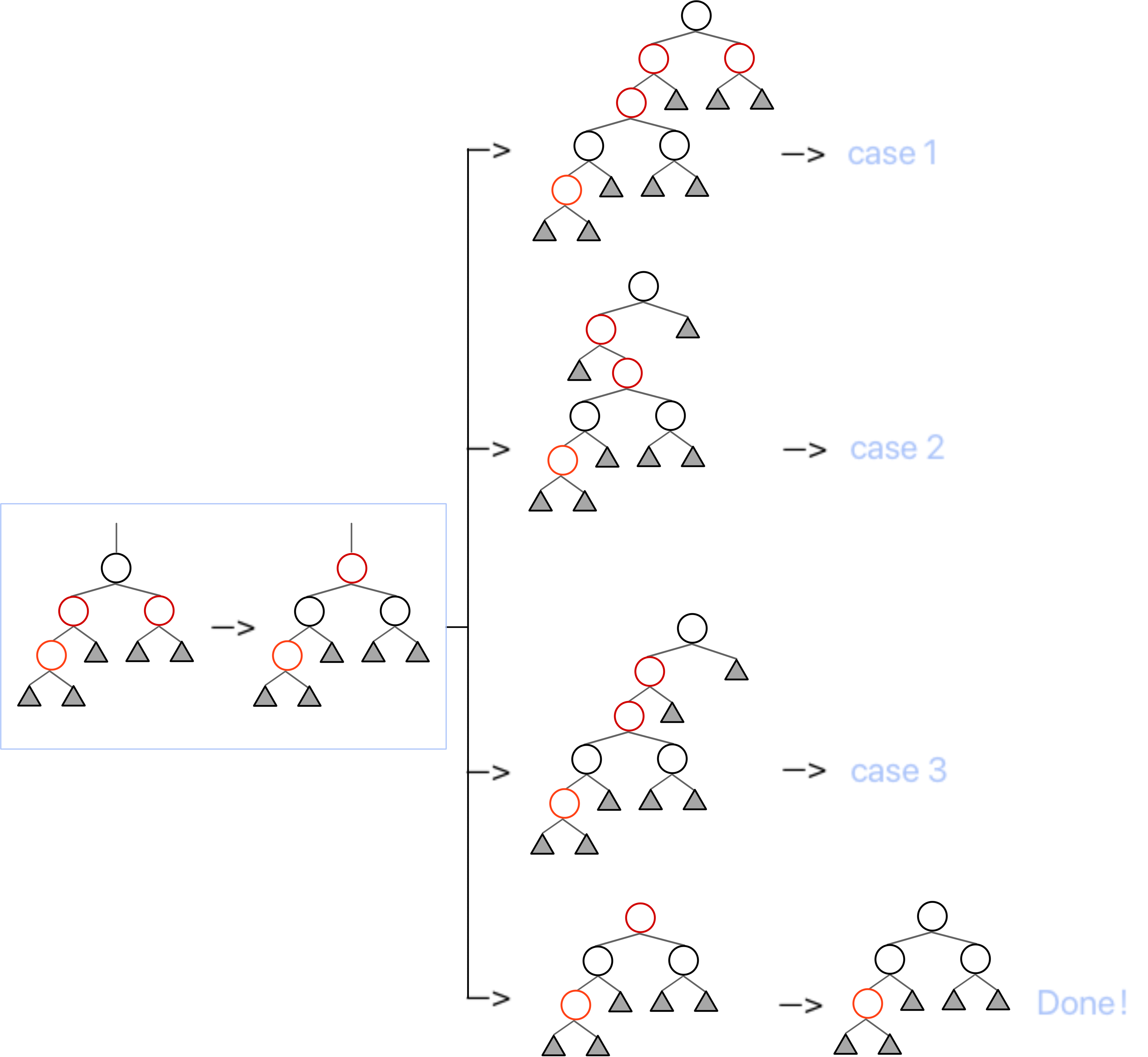
case1:
X的叔叔(即父亲的兄弟)是红色的这里所有的结点都带子树,至少会有NULL结点
解决方法:由于父结点P和叔叔结点U都是红色的,寻求爷爷结点G的帮忙,最后将父结点P和叔叔结点U染黑,爷爷结点染红本质在于将问题向上推,最差的情况也就是将问题一直推到根结点,此时只需要将根结点染黑即可
但是所有结点仍然满足性质,从该结点出发到后代叶结点的包含相同数量的黑结点
-
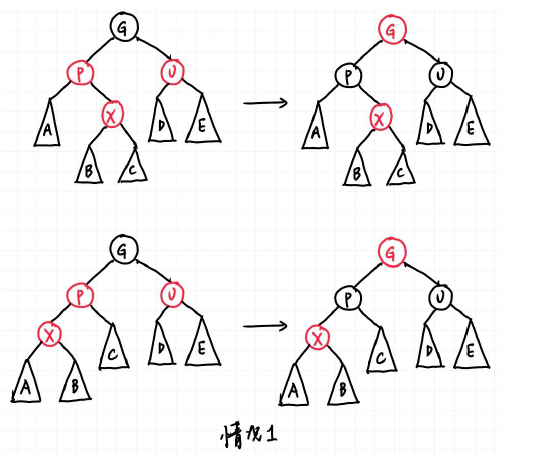
case2:
X的叔叔是黑结点,且X是P的右孩子 -
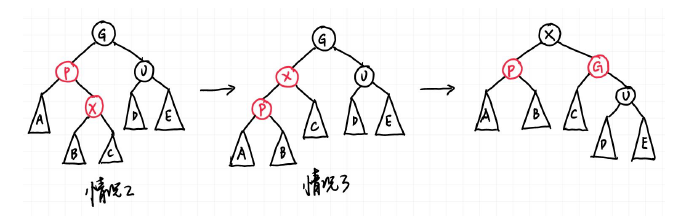
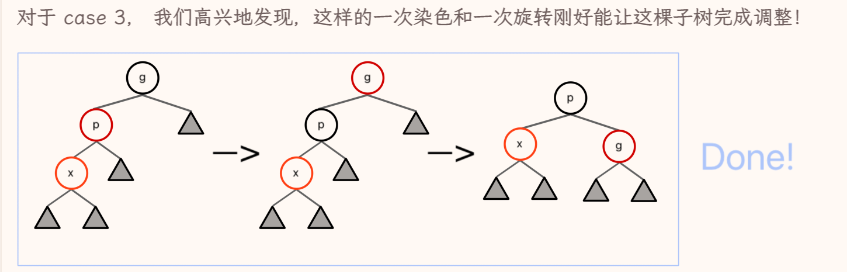
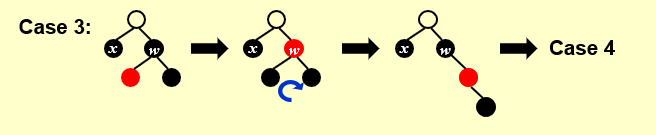
case3:
X的叔叔是黑结点,且X是P的左孩子对于case2到case3的转变,X绕P点进行右旋(RR rotation)
对于case3情况,G点绕X点进行左旋(LL rotation),成功解决问题
最后进行染色,根结点为黑色,第二层为红色
对于case2,可以是直接使用LR旋转,只需要保证最终根结点为黑色,第二层为红色
即如果插入后直接落入情况三,只需要一次旋转染色即可解决。直接落入情况二,一次旋转进入情况三,再一次旋转染色即可解决。但如果落入情况一,一次调整后可能还在情况一,可能直到最后都是通过情况一加上染黑根结点解决,也可能几次调整后进入情况二或三后解决。
定理: 一棵有n个内部结点的红黑树,插入一个结点的时间复杂度为\(O(logN)\)
根据上述流程,红黑树插入最多的旋转次数为2次(因为只有情况2 和3 会要旋转进入情况2 后1 次旋转必定进入情况3,进入情况3 后1 次旋转必定解决),改变颜色最多是\(O(logN)\)次,在情况2、3只需要染一次色,情况1最差也是每两层染一次色,因为我们已知红黑树的最大高度为\(O(logN)\)。
因此插入操作,除了\(O(logN)\)的搜索时间外,仅剩常数次的旋转和\(O(logN)\)次的染色,最后仍为\(O(logN)\)的时间复杂度
一定会有红色。数学归纳法进行证明
- 当\(n=2\)时,在黑色根结点的下方插入一个红结点,不产生任何负面影响,红色结点数+1
- 如果以后插入红结点后不需要调整,则红色结点数量增加
-
如果需要调整,也就是对应\(case1-3\)
- 对于case1,\(X,G\)一定为红色结点,即使 最后\(G\)不断向上推移到根结点后被染黑,\(X\)依然保持红色
- 对于case2,经过旋转,叔叔结点的近侄子变为远侄子,红色结点数不变
- 对于case3,再次旋转后,可以保证根结点为黑色,第二层均为红结点
2.1.2 Delete¶
不考虑红黑树,BST结点删除的回顾
-
Delete a leaf node: reset its parent link to NULL 如果X没有孩子,直接删除就好
-
Delete a degree 1 node: replace the node by its single child 如果X只有一个孩子,那让孩子接替X的位置
-
Delete a degree 2 node:
-
Replace the node by the largest one in its left subtree or the smallest one in its right subtree.
-
Delete the replacing node from the subtree.
如果X有两个孩子,那就让X与左子树的最大结点交换,然后删除X
此时X所在位置最多只有一个孩子结点,因为左子树的最大值没有右孩子,右子树的最小值没有左孩子 -
红黑树的删除在此基础上展开,对于第三种情况,X与左子树的最大值进行交换,
交换的仅仅是键值,颜色并没有交换,否则红结点可能换到根结点(虽然可以染黑),黑结点换到下方,极有可能造成性质5被破坏。并且第三种情况经过交换后,会直接转化为第一、第二种情况。
对于情况一,接替被删除结点的是NULL
对于情况二,被删除结点的子结点接替位置。如果被删除结点为红结点(似乎不太可能,性质5,红结点的两个子结点都为黑色,要么都为叶子,要么都不为)。如果删除的是黑色,接替上来是红色,染黑即可,性质5仍然满足。 接替上来是黑色,这该如何处理,显然沿着子树的路径,黑色结点数少了一
为了解决删除黑色,接替结点为黑色,沿子树路径黑色结点数减一 Must add 1 black to the path of the replacing node.
直接给替换上来的黑色再加一重黑色,变成双黑
以下X 在此处则表示双黑结点,图中用黑色圆圈和圆旁边的加号表示双黑,蓝色表示颜色无所谓,可红可黑。
- case1:X的兄弟是红色的
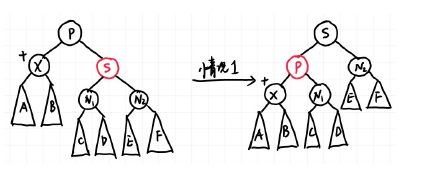 $$
父兄换色 + 右旋
$$
由于原先的树满足红黑树定义第四条,因此此时父结点一定是黑色。我们的想法很简单,兄弟是红色,那就希望兄弟能两肋插刀,把兄弟转上去,为了保持红黑树性质,很可惜只能把父亲染红,,自己还承受双黑debuff。但是好处在于,这个问题转化为了接下来的情况二三四中的一种,我们来看如何解决。
$$
父兄换色 + 右旋
$$
由于原先的树满足红黑树定义第四条,因此此时父结点一定是黑色。我们的想法很简单,兄弟是红色,那就希望兄弟能两肋插刀,把兄弟转上去,为了保持红黑树性质,很可惜只能把父亲染红,,自己还承受双黑debuff。但是好处在于,这个问题转化为了接下来的情况二三四中的一种,我们来看如何解决。
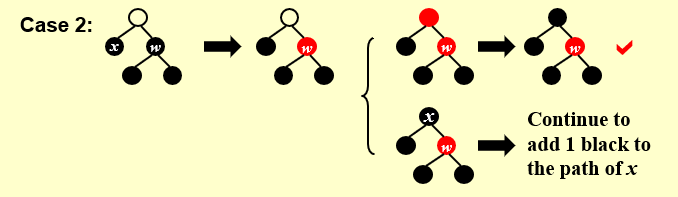
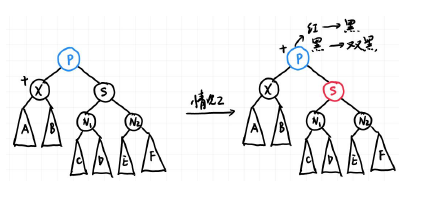
- case2:X的兄弟是黑色的,且兄弟的两个孩子(根据远近划分为远侄子和近侄子)都是黑色的
现在这个情况从P视角出发,满足性质5。所以为了缓减双黑这个debuff,我将双黑推给父亲,这时性质5被打破了,兄弟被迫变为红色
- 如果父结点本身为红色,
在双黑加持下,变为黑色,恰好弥补黑色少一的情况,问题解决 - 如果父结点本身为黑色,那就变为双黑,问题向根结点靠近
-
假如从case1变为case2,父结点一定为红色,那么问题直接解决
-
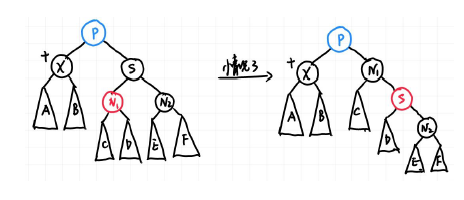
case3 : X的兄弟结点是黑色,但是近侄子是红色的,远侄子是黑色的
此时的红色在父亲\(P\)的\(RL\)位置上,因此实现double rotation中的一个single rotation(左旋)就能得到\(RR\)情况
并且此处存在颜色变换
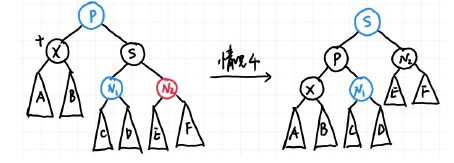
- case4 : X 的兄弟是黑色的,且远侄子是红色的,近侄子颜色任意
此时对应AVL树的RR,于是再一次single rotation即可把双黑的一重黑丢给红色远侄子(即\(X,N_2\)都变成黑色),但为了保证红黑树性质的颜色变换,P和S还要交换颜色
定理: 一棵有n个内部结点的红黑树删除一个结点的时间复杂度为\(O(logN)\)
- 我们最多使用\(O(logN)\)的时间找到删除结点,进行一次交换,后续进行删除操作
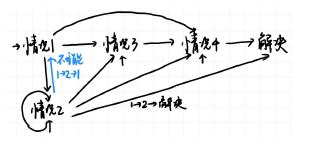
- 最坏进入删除黑色,接替点为黑色的情况,对于case1,如果进入case3,case4能快速解决,因为4 可以直接解决,3 直接进入4 然后解决。如果进入case2,也因为父结点为红色直接解决。
- 对于case2,可以因为父结点为红色直接解决,也能多次多次进入case2,每次向上推一格,由于树高为\(O(logN)\),所以最多进行\(O(logN)\)次
- 对于case3,case4,均能快速解决。
2.2 B+ Tree¶
B+ 树是一种用树状形式维护有序数列比较信息的数据结构,其增改操作拥相对于二叉树结构更加稳定的对数时间复杂度,通常用于数据库和操作系统的文件系统中。
A B+ tree of order M is a tree with the following structural properties:
- The root is either a leaf or has between 2 and \(M\) children. 根要么是叶子,要么具有 2 和\(M\) 子级。
- All nonleaf nodes (except the root) have between$ ⌈M/2⌉$and M children. 所有非叶结点(根除外)都有 ⌈M/2⌉ 和 M 个子结点。
- All leaves are at the same depth. 所有叶子都处于相同的深度。
所有真实的数据都被存储在叶子结点中,形成一个有序的数列。而非叶子结点(不包含root)中第$i$个值等于第$i+1$颗子树的最小值。如上图所示表现为颜色相同的一对上下结点。因此非叶结点最多存 $M-1$个值。
抽象地来说就是,我们把一个数列相对均匀的分为 \(m\)块,然后把分界的数拿出来。当我们去查找或插入时,只需要和这些边界数进行比较,就知道它应该放在哪一块里。再不断细化粒度,用类似于\(m\)分”的思想来找到目标位置。
由于它在空间最浪费的情况下是一棵 \(\lceil M/2 \rceil\) 叉树,所以 B+ 树的深度是 \(O(\lceil \log_{\lceil M/2 \rceil} N \rceil)\)。
2.2.1 查找¶
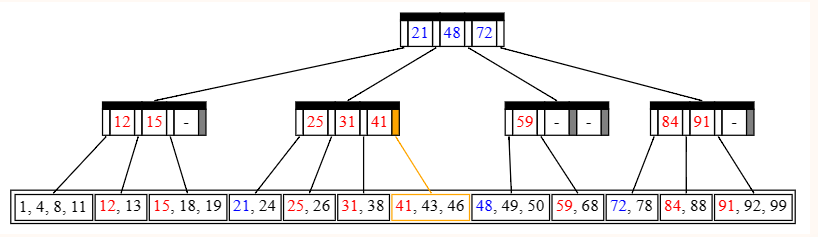
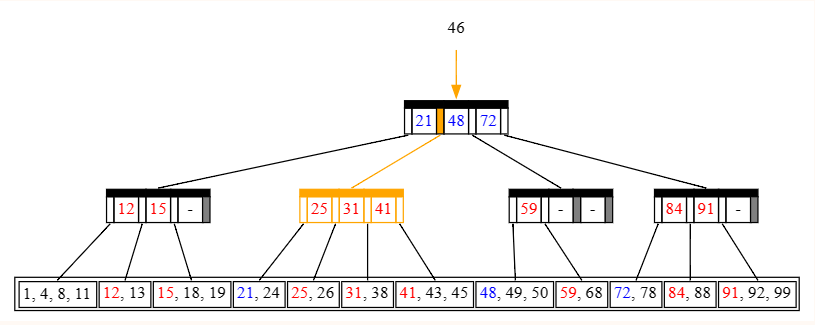
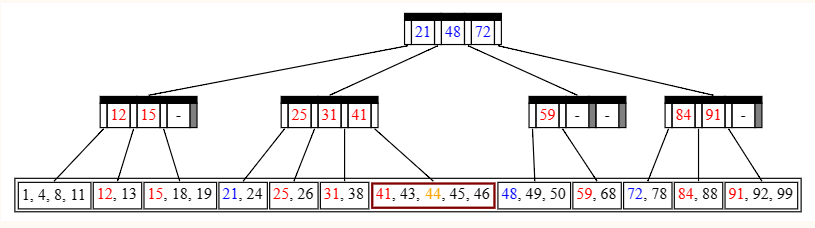
例如,我们在上面这棵树中找 43 这个值,橙色部分表示我们的焦点。
我们发现有 21≤43<48,所以顺着标识的橙色指针向下。
我们发现有 41≤43,所以顺着标识的橙色指针向下
已经走到叶子结点,最后发现我们要找的 43。
2.2.2 插入¶
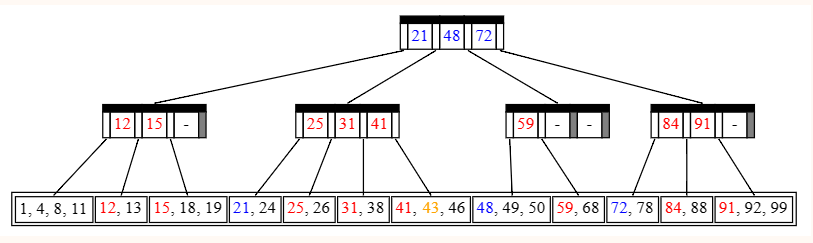
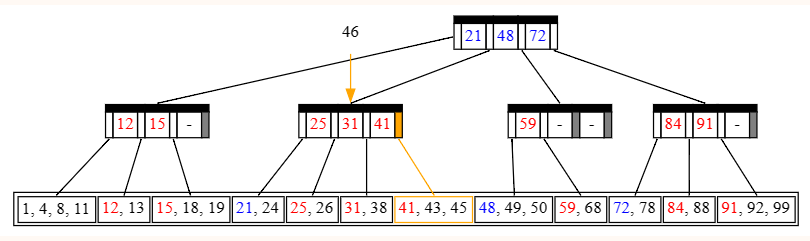
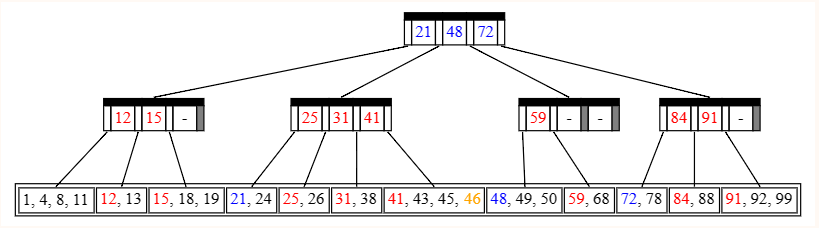
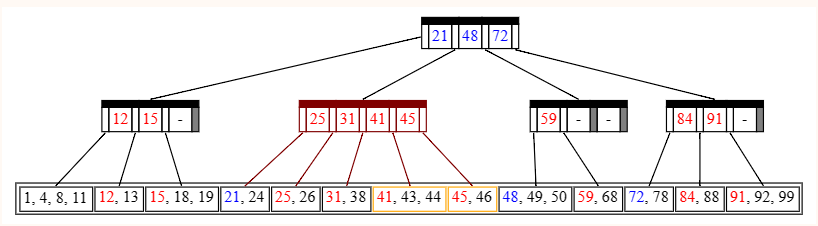
Insert(46), no split
找到要塞的位置了,发现要塞的地方是 45 的后面,插入以后发现一共 4 个数,而 �=4M=4,不需要分裂。
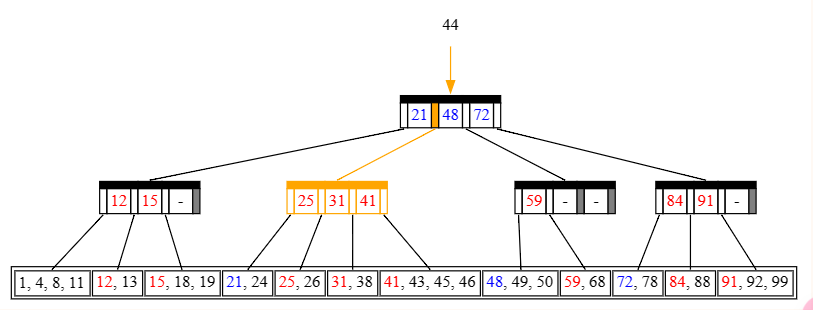
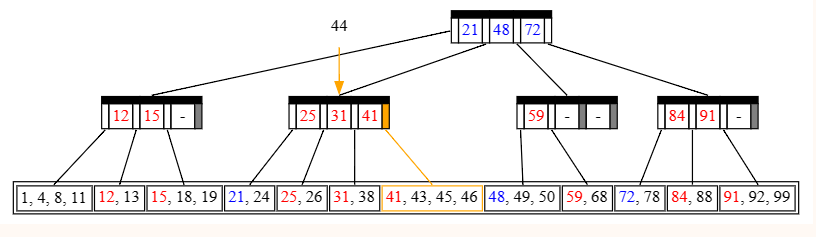
Insert(44), split
找到要塞的位置了,发现要塞的地方是 45 的前面,插入以后发现一共 5 个数,而 �=4M=4,需要分裂!
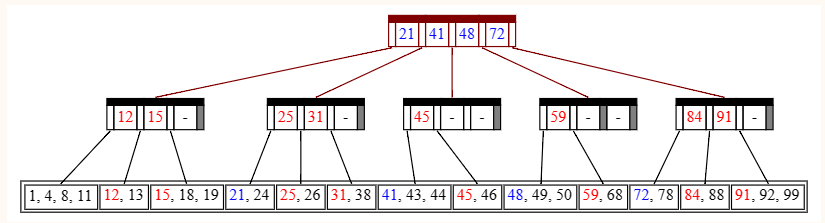
向上递归,我们悲痛地发现,这个节点在分裂后有了 5 个子节点,不得不再次分裂。
向上递归,我的老天爷呀,怎么还没到头!这下我们要分裂根部了!
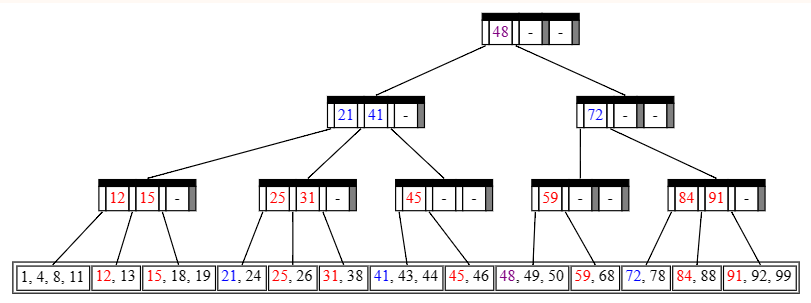
由于根部被裂开了,所以我们需要添加一个新的根,这也意味着树的层数增高了。
现在,我们终于完成了插入。