5. Binomial Queue¶

约 2631 个字 337 行代码预计阅读时间 17 分钟

为什么需要二项堆？

二项堆的引入来源于我们希望插入建堆的操作有常数的平均时间。因为二项堆能够实现在$O(N)$的时间内实现$n$个结点的插入操作。

5.1 概念¶

A binomial queue is not a heap-ordered tree, but rather a collection of heap-ordered trees, known as aforest. Each heap-ordered tree is a binomial tree.

二项式队列不是堆有序树，而是堆有序树的集合，称为森林。每个堆排序树都是一个二项式树。

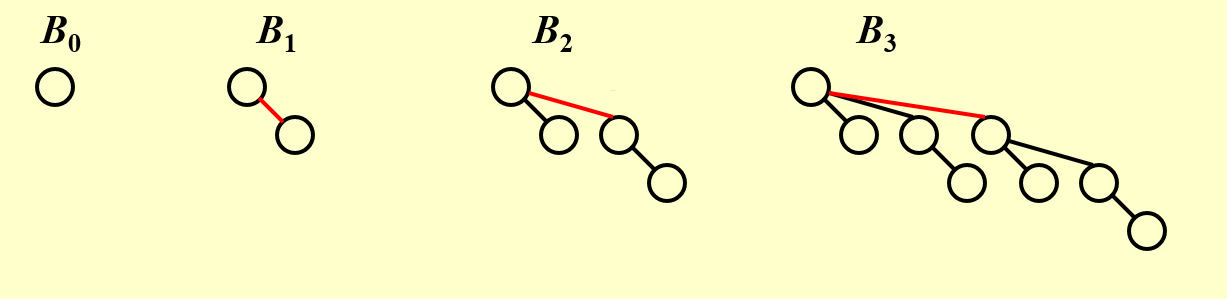
A binomial tree of height 0 is a one-node tree.

A binomial tree, $B_k$, of height k is formed by attaching a binomial tree, $B_{k – 1}$, to the root of another binomial tree,$B_{k – 1}$.

二项堆的定义如下：

结构性质
- 二项堆不再是一棵树，而是多棵树构成的森林，其中每一棵树都是二项树
- 一个二项堆中的每一棵二项树都具有不同的高度，即每一高度最多对应一颗二项树
- 高度为0的二项树是一个单节点树。高度为k的二项树$B_k$通过将一棵二项树$B_{k-1}$连接到另一棵二项树$B_{k-1}$的根上形成。
序性质：

每一棵二项树都保持堆的序性质（有序堆），对于最小堆——孩子结点大于父亲结点

\[ (a+b)^n = \sum_{i= 1} ^n C_n ^i a^{n-i}b^i \]

从图中我们可以观察出二项树$B_k$实际上是由一个root加上$B_0,B_1,...B_{k-1}$组成

用数学归纳法证明 $B_k$ 有 $2^k$个结点

当k=0时，显然一个结点成立
当k=m时，假设条件成立。那么当k=m+1时，

$B_{m+1}$的结点数是$2^0+2^1+...+2^m + 1 = 2 ^{m+1} - 1 + 1 = 2 ^{m+1}$

用数学归纳法证明在深度为$d$的结点数恰好是二项系数$C_n ^d$

根据二项树的定义：B_k是由两个B_{k-1}形成的，且两棵树存在深度差1

\[ \begin{aligned} &C_{n}^0 = C_{n+1}^0 = 1\\ &C_{n}^1 + C_{n}^0 = C_{n+1}^1 = n+1\\ &....\\ &C_n^i + C_n^{i-1} = C_{n+1}^i \end{aligned} \]

$B_k$ structure + heap order + one binomial tree for each height

A priority queue of any size can be uniquely represented by a collection of binomial trees.

5.2 操作¶

5.2.1 FindMin¶

The minimum key is in one of the roots.

There are at most $logN$ roots, hence $Tp$ =$O(logN)$.

最小值在二项队列的某一个根结点，只需遍历所有的root

We can remember the minimum and update whenever it is changed. Then this operation will take O(1).

设置专门记录最小根结点的结点，只需要在DeleteMin或则Insert 一个新的最小值后更新这个临时结点即可。时间复杂度为$O(1)$

5.2.2 Merge¶

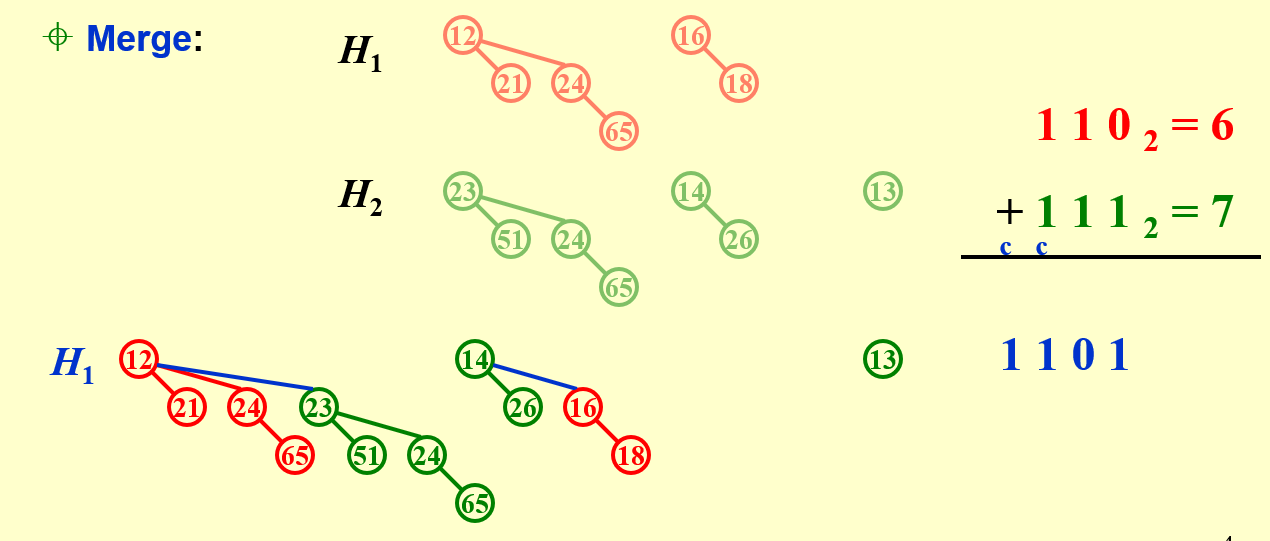
每一个二项堆都有一个唯一对应的二进制数。那么合并二项堆实际上可以等价于二进制数的加法。

从最小的二项树开始（也就是二进制的最低位），如果无需进位（0+1，1+0）则直接留下作为新堆的一部分。如果需要进位(1+1)，在合并后与下一位做加法，如此循环到最高位完成操作。

在保证堆的存储顺序是按高度从小到大排列的前提（这样就不用先遍历所有的堆，找到最小的堆。而是直接从开头进行合并）下，时间复杂度很显然就是$O(log n)$，因为就是二进制逐位做操作,只需要计算一共有多少二进制位即可，O（logN）

Must keep the trees in the binomial queue sorted by height.

相应$B_k$ merge的时候，需要满足heap上小下大的要求。root大的作为root小的子树

// 二项树的合并
BinTree MergeTrees(BinTree T1, BinTree T2)
{
    // merge equal size trees
    // attach the larger one to the smaller one
    if(T1->Element > T2->Element)
        return MergeTrees(T2, T1);
    // T2 is larger, attach T2 to T1
    T2->NextSibling = T1->LeftChild;
    T1->LeftChild = T2;
    return T1;
}
// 二项队列的合并
BinQueue Merge(BinQueue H1, BinQueue H2)
{
    BinTree T1, T2, Carry = NULL;
    if(H1->currentsize + H2->currentsize > 100)
        cout << "Merge would exceed max tree capacity!" << endl;
    H1->currentsize += H2->currentsize;
    for(int i = 0, j = 1; j <= H1->currentsize; i++, j *= 2)
    {
        T1 = H1->TheTrees[i];
        T2 = H2->TheTrees[i];
        switch(4 * !!Carry + 2 * !!T2 + !!T1)
        {
            // Carry T2 T1
            case 0: // 000 no tree
                break;
            case 1: // 001 only T1
                break;
            case 2: // 010 only T2
                H1->TheTrees[i] = T2;
                H2->TheTrees[i] = NULL;
                break;
            case 3: // 011 T1 and T2
                Carry = MergeTrees(T1, T2);
                H1->TheTrees[i] = H2->TheTrees[i] = NULL;
                break;
            case 4: // 100 only Carry
                H1->TheTrees[i] = Carry;
                Carry = NULL;
                break;
            case 5: // 101 Carry and T1;
                Carry = MergeTrees(Carry, T1);
                H1->TheTrees[i] = NULL;
                break;
            case 6: // 110 Carry and T2
                Carry = MergeTrees(Carry, T2);
                H2->TheTrees[i] = NULL;
                break;
            case 7: // 111 all three
                H1->TheTrees[i] = Carry;
                Carry = MergeTrees(T1, T2);
                H2->TheTrees[i] = NULL;
                break;
        }
    }
    return H1;
}

这里使用!!的目的是将指针bool化，如果T1存在，!!T1就等于1，如果T2不存在，那么!!T2就等于0
然后我们就能理解$4\times !!Carry + 2\times !!T2+!!T1$ 的含义了，事实上这就是一个三位二进制数（当然case 的标号还是十进制的，但我们心里要转化为二进制来分析），最高位表示是否有carry，即之前的合并是否带来了进位（从堆的角度看也就是之前合并出了一棵新的更高的二项树），第二位代表第二个堆H2是否有高度为i 的二项树，最后一位代表H1 是否有高度为i 的二项树。
不同case对应的情况
- 000：什么都不用做
- 001：$T1$存在，既然返回的就是$H1$，所以什么都不用做
- 010：$T2$存在，但是由于返回的是$H1$，需要将$H2$中的树转移到$H1$中对应的树，同时$H2$对应的树需要置为NULL
- 011：$T1$，$T2$都存在，此时会产生carry，$H1$ 和 $H2$ 当前位变为NULL，进位等于两个堆该高度的二项树合并后的结果
- 100：仅仅carry存在，类比010
- 101：$H1$ 当前位变为NULL，新的carry 等于$T1$ 和当前的carry 合并的结果
- 110：$H2$ 当前位变为NULL，新的carry 等于$T2$ 和当前的carry 合并的结果
- 111：此让$H1$ 当前位变为carry，新的carry 等于$T1$ 和$T2 \(合并的结果，最后给$H2\) 当前位变为NULL 即可。

5.2.3 Insert¶

看作是merge的special case

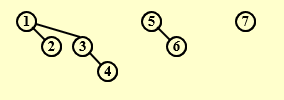
【Example】Insert 1, 2, 3, 4, 5, 6, 7 into an initially empty queue.

1，2 形成一个$B_1$
3，4形成一个$B_1$，与前面的1，2 merge 形成$B_2$
5，6形成一个$B_1$
7形成一个$B_0$

BinQueue Insert(BinQueue H1, int x)
{
    BinQueue OneItem;
    BinTree T;
    OneItem = Initialize();
    T = new BinNode;
    if(T == NULL)
        cout << "Out of space!" << endl;
    T->Element = x;
    T->LeftChild = T->NextSibling = NULL;
    OneItem->TheTrees[0] = T;
    OneItem->currentsize = 1;
    return Merge(H1, OneItem);
}

5.2.4 DeleteMin¶

时间复杂度为$O(log N)$

在根结点找到最小值，然后把最小值所在的树单独拿出分裂为二项队列，然后把这个新的二项队列与原二项队列进行合并。每一个过程的时间复杂度为$O(logN)$。故加起来的时间复杂度仍为$O(logN)$。

int DeleteMin(BinQueue H)
{
    BinQueue DeletedQueue;
    Position DeletedTree, OldRoot;
    int MinItem = 1000000;
    int i, j, MinTree;
    // MinTree is the index of thr tree with the minimum item
    if(Isempty(H))
    {
        cout << "Empty binomial queue!" << endl;
        return -1;
    }
    // 1. find the tree with the minimum item
    for(i = 0; i < MaxTrees; i++)
    {
        if(H->TheTrees[i] && H->TheTrees[i]->Element < MinItem)
        {
            MinItem = H->TheTrees[i]->Element;
            MinTree = i;
        }
    }
    DeletedTree = H->TheTrees[MinTree];
    // 2. remove the MinTree from H
    H->TheTrees[MinTree] = NULL;
    // 3. remove the MinItem from the MinTree
    // and store the rest of the MinTree in DeletedQueue
    OldRoot = DeletedTree;
    DeletedTree = DeletedTree->LeftChild;
    delete OldRoot;
    DeletedQueue = Initialize();
    // 对于索引为i的树，其包含的节点数为2^i
    DeletedQueue->currentsize = (2 ^ MinTree) - 1;
    for(j = MinTree - 1; j >= 0; j--)
    {
        DeletedQueue->TheTrees[j] = DeletedTree;
        DeletedTree = DeletedTree->NextSibling;
        DeletedQueue->TheTrees[j]->NextSibling = NULL;
    }
    H->currentsize -= DeletedQueue->currentsize + 1;
    H = Merge(H, DeletedQueue);
    return MinItem;
}

5.3 二项队列的实现¶

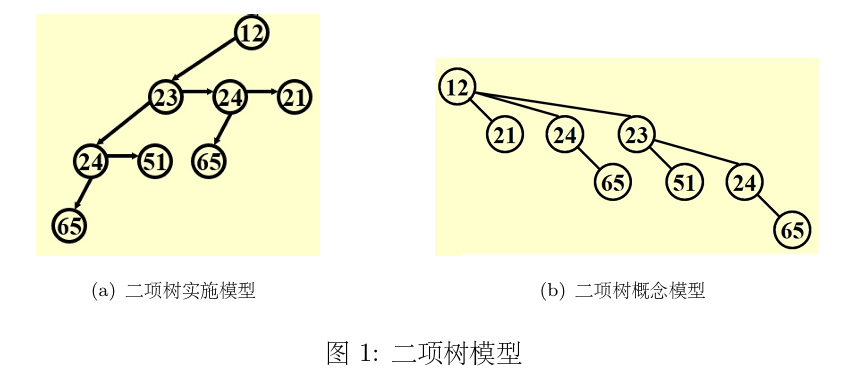
为什么使用左儿子右兄弟模型？

因为每一个结点的孩子数量可能大于2个

要从根结点12开始快速遍历三个子树（21，24，23），要用“左孩子右兄弟的实现方式，对应12->23->24->21

图(b)$B_3$是两棵$B_2$的合并结果，为什么合并之后需要按照子树的大小（结点数）降序排列呢？

根结点为12和23的两棵树合并时，23会成为12的子树。按照左儿子右兄弟的模型，应该将23插入到子树的链表。

如果按照升序的话，需要先遍历所有的子结点(21,24),才能将最大子树$B_2$加上，多出来遍历的开支。

#include "BinTree.h"

using namespace std;

// #define MaxTrees 10

// typedef struct BinNode
// {
//     int Element;
//     // 左儿子右兄弟
//     Position LeftChild;
//     Position NextSibling;
// }*BinTree, *Position;

// typedef struct Collection
// {
//     // total number of nodes
//     int currentsize;
//     BinTree TheTrees[MaxTrees];
// }*BinQueue;

// int IsEmpty(BinQueue H);
// BinQueue Initialize();
// BinTree MergeTrees(BinTree T1, BinTree T2);
// BinQueue Insert(BinQueue H1, int x);
// BinQueue DeleteMin(BinQueue H);
// void PrintQueue(BinQueue H);


int Isempty(BinQueue H)
{
    return H->currentsize == 0 || H == NULL;
}

BinQueue Initialize()
{
    BinQueue H = new Collection;
    if(H == NULL)
        cout << "Out of space!" << endl;
    H->currentsize = 0;
    for(int i = 0; i < MaxTrees; i++)
        H->TheTrees[i] = NULL;
    return H;
}

BinTree MergeTrees(BinTree T1, BinTree T2)
{
    // merge equal size trees
    // attach the larger one to the smaller one
    if(T1->Element > T2->Element)
        return MergeTrees(T2, T1);
    // T2 is larger, attach T2 to T1
    T2->NextSibling = T1->LeftChild;
    T1->LeftChild = T2;
    return T1;
}

BinQueue Merge(BinQueue H1, BinQueue H2)
{
    BinTree T1, T2, Carry = NULL;
    if(H1->currentsize + H2->currentsize > 100)
        cout << "Merge would exceed max tree capacity!" << endl;
    H1->currentsize += H2->currentsize;
    for(int i = 0, j = 1; j <= H1->currentsize; i++, j *= 2)
    {
        T1 = H1->TheTrees[i];
        T2 = H2->TheTrees[i];
        switch(4 * !!Carry + 2 * !!T2 + !!T1)
        {
            // Carry T2 T1
            case 0: // 000 no tree
                break;
            case 1: // 001 only T1
                break;
            case 2: // 010 only T2
                H1->TheTrees[i] = T2;
                H2->TheTrees[i] = NULL;
                break;
            case 3: // 011 T1 and T2
                Carry = MergeTrees(T1, T2);
                H1->TheTrees[i] = H2->TheTrees[i] = NULL;
                break;
            case 4: // 100 only Carry
                H1->TheTrees[i] = Carry;
                Carry = NULL;
                break;
            case 5: // 101 Carry and T1;
                Carry = MergeTrees(Carry, T1);
                H1->TheTrees[i] = NULL;
                break;
            case 6: // 110 Carry and T2
                Carry = MergeTrees(Carry, T2);
                H2->TheTrees[i] = NULL;
                break;
            case 7: // 111 all three
                H1->TheTrees[i] = Carry;
                Carry = MergeTrees(T1, T2);
                H2->TheTrees[i] = NULL;
                break;
        }
    }
    return H1;
}
BinQueue Insert(BinQueue H1, int x)
{
    BinQueue OneItem;
    BinTree T;
    OneItem = Initialize();
    T = new BinNode;
    if(T == NULL)
        cout << "Out of space!" << endl;
    T->Element = x;
    T->LeftChild = T->NextSibling = NULL;
    OneItem->TheTrees[0] = T;
    OneItem->currentsize = 1;
    return Merge(H1, OneItem);
}
int DeleteMin(BinQueue H)
{
    BinQueue DeletedQueue;
    Position DeletedTree, OldRoot;
    int MinItem = 1000000;
    int i, j, MinTree;
    // MinTree is the index of thr tree with the minimum item
    if(Isempty(H))
    {
        cout << "Empty binomial queue!" << endl;
        return -1;
    }
    // 1. find the tree with the minimum item
    for(i = 0; i < MaxTrees; i++)
    {
        if(H->TheTrees[i] && H->TheTrees[i]->Element < MinItem)
        {
            MinItem = H->TheTrees[i]->Element;
            MinTree = i;
        }
    }
    DeletedTree = H->TheTrees[MinTree];
    // 2. remove the MinTree from H
    H->TheTrees[MinTree] = NULL;
    // 3. remove the MinItem from the MinTree
    // and store the rest of the MinTree in DeletedQueue
    OldRoot = DeletedTree;
    DeletedTree = DeletedTree->LeftChild;
    delete OldRoot;
    DeletedQueue = Initialize();
    // 对于索引为i的树，其包含的节点数为2^i
    DeletedQueue->currentsize = (2 ^ MinTree) - 1;
    for(j = MinTree - 1; j >= 0; j--)
    {
        DeletedQueue->TheTrees[j] = DeletedTree;
        DeletedTree = DeletedTree->NextSibling;
        DeletedQueue->TheTrees[j]->NextSibling = NULL;
    }
    H->currentsize -= DeletedQueue->currentsize + 1;
    H = Merge(H, DeletedQueue);
    return MinItem;
}
void PrintTree(BinTree T)
{
    // 关于左儿子右兄弟的遍历
    // 一行一行的输出
    queue<BinTree> line1;
    queue<BinTree> line2;
    line1.push(T);
    while(!line1.empty())
    {
        BinTree temp = line1.front();
        line1.pop();
        cout << temp->Element << " ";
        if(temp->LeftChild)
            line2.push(temp->LeftChild);
        while(temp->NextSibling)
        {
            cout << temp->NextSibling->Element << " ";
            if(temp->NextSibling->LeftChild)
                line2.push(temp->NextSibling->LeftChild);
            temp = temp->NextSibling;
        }
        if(line1.empty())
        {
            cout << endl;
            swap(line1, line2);
        }
    }
}
void PrintQueue(BinQueue H)
{
    for(int i = 0; i < MaxTrees; i++)
    {
        if(H->TheTrees[i])
        {
            cout << "Tree " << i << ": "<< endl;
            PrintTree(H->TheTrees[i]);
        }
    }
    cout << "--------------------------\n";
}

int main()
{
    BinQueue H1 = Initialize();
    H1 = Insert(H1, 12);
    H1 = Insert(H1, 21);
    H1 = Insert(H1, 24);
    H1 = Insert(H1, 65);
    H1 = Insert(H1, 23);
    H1 = Insert(H1, 51);
    H1 = Insert(H1, 24);
    H1 = Insert(H1, 65);
    H1 = Insert(H1, 14);
    H1 = Insert(H1, 26);
    H1 = Insert(H1, 16);
    H1 = Insert(H1, 18);
    H1 = Insert(H1, 13);
    PrintQueue(H1);
    int MinItem = DeleteMin(H1);
    PrintQueue(H1);
    cout << "MinItem: " << MinItem << endl;
}

5.4 摊还分析¶

A binomial queue of N elements can be built by N successive insertions in O(N) time.

插入最坏的情况是$O(log N)$,但是坏操作带来进位的同时，后续会带来很多的0，也就没有进位

5.4.1 聚合法¶

聚合法需要每一步的操作复杂度。关于合并的时间复杂度实际上与二进制的加法有对应关系。包含加法和进位，对应就是插入和merge。这两种情况都对应常数时间复杂度。

从空树连续插入n个顶点的时间复杂度为 n + 进位的次数。

最低位每次加1都会merge(对应单纯的插入)，次低位每两次插入会merge（对应进位），以此类推，计算n次插入造成的merge次数 $$ n + \dfrac{n}{2} + \dfrac{n}{4}+...+\dfrac{n}{2^{logn +1}} $$ 根据等比数列的求和，显然上述的时间复杂度不会超过2n，所以单步操作的摊还时间成本就是常数级的。

此处的total link可以理解为：

每两次发生一次$B_0->B_1$的link，每四次发生一次$B_1->B_2$的link，依次类推$N(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+....)$

5.4.2 势能法¶

分析得到

link=1，不会造成二项树的增加（$B_0 \rightarrow B_1$）。
link=2，会造成二项树数量减1($B_0\rightarrow B_1 \rightarrow B_2$),原先的$B_0,B_1$被转化为$B_2$
依次类推，link=3，会造成二项树的数量减2

每一步的时间复杂度为step+link，得到如果一次插入的时间复杂度为k，那么二项队列中的二项树将减少$（k-2）$

记$c_i$表示实际上每一步插入的成本

记$\Phi_i$表示在第i次插入完成后，二项队列中二项树的数量

那么每次的摊还成本就是 $$ \widehat c_i = c_i + \Phi_i - \Phi_{i-1} = c_i + (2-c_i) = 2 $$

5.5 习题集¶

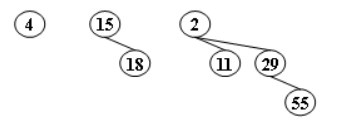
Delete the minimum number from the given binomial queues in the following figure. Which one of the following statements must be FALSE?
- A. there are two binomial trees after deletion, which are $B_1$ and $B_2$
- B. 11 and 15 can be the children of 4
- C. 29 can never be the root of any resulting binomial tree
- D. if 29 is a child of 4, then 15 must be the root of $B_1$
此处说明进位carry和H1，H2的计算方式是不固定的，可以自由组合，得到不同的结果
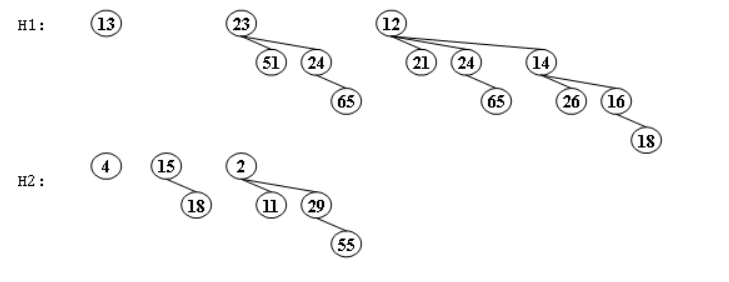
Merge the two binomial queues in the following figure. Which one of the following statements must be FALSE?
- A. there are two binomial trees after merging, which are $B_2$ and $B_4$
- B. 13 and 15 are the children of 4
- C. if 23 is a child of 2, then 12 must be another child of 2
- D. if 4 is a child of 2, then 23 must be another child of 2
Inserting a number into a binomial heap with 15 nodes costs less time than inserting a number into a binomial heap with 19 nodes.

False

$15 = 1111_2, 19 = 10011_2$

显然插入到19个node的二项堆发生的进位次数少
To implement a binomial queue, the subtrees of a binomial tree are linked in increasing sizes.

False

按照子树大小（结点数）降序排列
The potential function Q of a binomial queue is the number of the trees. After merging two binomial queues $H1$ with 12 nodes and $H2$ with 13 nodes，what is the potential change $Q(H1+H2)−(Q(H1)+Q(H2))$ ?

\[ 12 = 1100_2\\ 13 = 1101_2\\ 12 + 12 = 11001\\ \Delta Q = 3 - 2 -3 = -2 \]
Making N insertions into an initally empty binomial queue takes$ Θ(NlogN)$ time in the worst case. False

插入的最坏情况是$logN,$ 这是因为需要一直进位上去。而N组数据不可能每插入一个就进位，因此是O(N)
After deleting number 14 from a binomial queue of 5 numbers { 12, 13, 14, 23, 24 }, which of the followings is impossible? A.the LeftChild link of the node 12 is NULL;

B. the NextSibling link of the node 12 is NULL;

C. the NextSibling link of node 13 may point to node 23;

D. the LeftChild link of node 24 is NULL;

优先队列里面，只有上下的大小限制，左右谁大谁小没有要求。因此，12一定是根，24一定是最下面的那个，A12一定是有孩子的，错。