跳转至

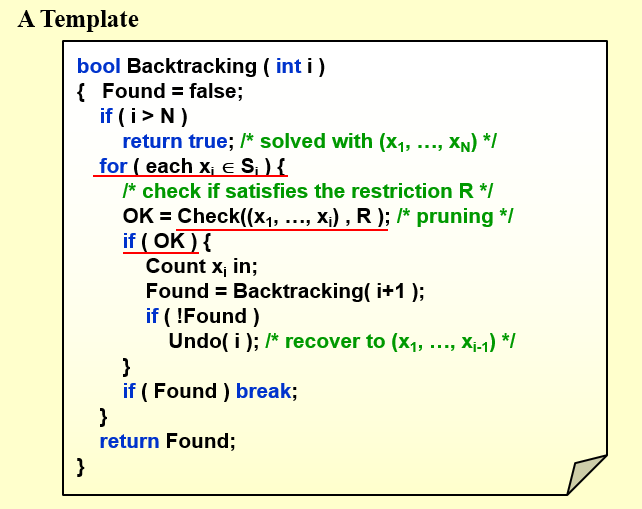
6. Backtracking

约 1312 个字 477 行代码 预计阅读时间 13 分钟

6.1 basic idea

找到问题答案的一个可靠方法是列出所有候选答案，回溯使我们能够消除对大量候选者的显式检查(剪枝操作)，同时仍然保证在算法运行到终止时会找到答案。

basic idea：回溯的历程

生成解，已经生成了前i个解\(((x_1,x_2,...,x_i)),(x_k∈S_k(解空间))\)

要添加新元素\((x_{i+1}^{(1)}∈X_{i+1}(第i个解集))\)

检查是否满足要求,若满足要求则生成解\(((x_1,x_2,...,x_i,x_{i+1}))\)

若不满足则找另一个\((x_{i+1}),若所有的(x_{i+1})\)都不满足条件,那么进行回溯

解变为\(((x_1,x_2,...,x_{i-1}))\)并且标记当前的\((x_i)\)为无效解换下一个\((x_i),\)以此类推

image-20240401112000643

6.2 八皇后问题

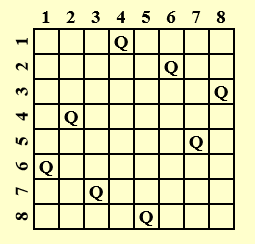
  • 【描述】在棋盘中找到八个位置放置皇后，使得它们都不同行且不同列，也不能同时位于对角线上

    image-20240401102133333

    \(Q_i\) 表示 queue in the i th row

    \(x_i\) 表示 the column index in which \(Q_i\) is $$ solution = (x_1, x_2, x_3, ... x_8) = (4,6,8,2,7,1,3,5) $$

限制条件：

  1. \(S_i\) = { 1,2,3,4,5,6,7,8 } for 1 <=i <= 8

  2. \(x_i != x_j \ if i \ != j\)

    不能在同一行和同一列

    This implies that the solution must be a permutation of 1, 2, ... , 8. Thus the number of candidates in the solution space is reduced to 8!.

  3. \((x_i - x_j) / (i - j) != |1|\)

    不能在对角线和反对角线上

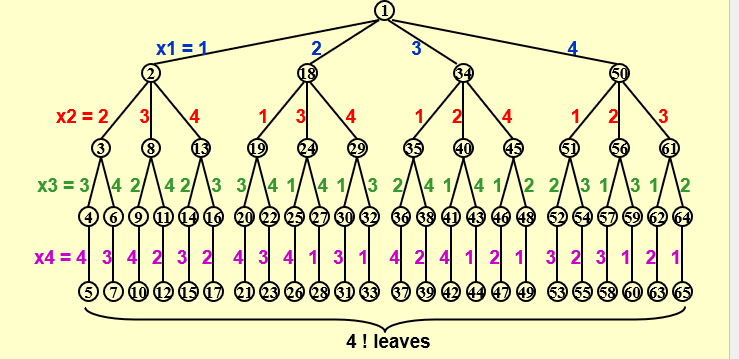
Method: 以4个皇后为例

step 1： 建立一棵game tree

image-20240401103030749

Each path from the root to a leaf defines an element of the solution space.

step 2：执行深度优先搜素，来检查路径是否正确

  1. 假设x1在第一列，顺序向下，x2 = 2，显然在对角线上，回溯至x1 = 1
  2. 后续向下，x2 = 3， 显然后续不管x3是在第二列还是第四列都会与x2在对角线上。回溯至x1 = 1
  3. 向下 x2 =4， 如果后续x3 = 2， x4 =3,在对角线上。如果x3 = 3，x3会与x2在对角线上。
  4. x1 = 1所有的情况均无法满足条件，继续向上回溯，转化为x1 = 2
#include<iostream>
#include<vector>
#include<cmath>

using namespace std;

// 用于控制皇后的数量，棋盘的规模
const int n = 8;

bool Is_safe(vector<int> &board, int row, int col)
{
    // check if there is a queen in the same column
    // or in the same diagonal
    // or in the same anti-diagonal
    // row means the row we are going to put a queen
    // col means the column we are going to put a queen
    // 此时需要用当前的queue的位置和之前的queue的位置进行比较
    for(int i = 0; i < row; i++)
    {
        if(board[i] == col || abs(board[i] - col) == abs(i - row))
        {
            return false;
        }
    }
    return true;
}

void SolveNQueens(int row, vector<int> &board, vector<vector<int>> &solutions)
{
    // row表示当前要放置皇后的行数
    if(row == n)
    {
        // 说明已经找到了一个解
        solutions.push_back(board);
        return;
    }
    // 每一行的皇后的位置都是从0到n-1
    // 判断当前的位置是否合法
    for(int col = 0; col < n; col++)
    {
        if(Is_safe(board, row, col))
        {
            board[row] = col;
            SolveNQueens(row + 1, board, solutions);
        }
    }
}
int main()
{
    // 初始化棋盘，-1表示没有皇后
    // board[i] = j 表示在(i, j)的位置有一个皇后
    vector<int> board(n, -1);
    // 用于存储所有的解
    vector<vector<int>> solutions;
    // 执行回溯算法
    SolveNQueens(0, board, solutions);
    // 输出所有的解
    for(auto solution : solutions)
    {
        for(auto pos: solution)
        {
            cout << pos << " ";
        }
        cout << endl;
    }
    cout << "Total solutions: " << solutions.size() << endl;
    return 0;
}

6.3 高速公路收费问题

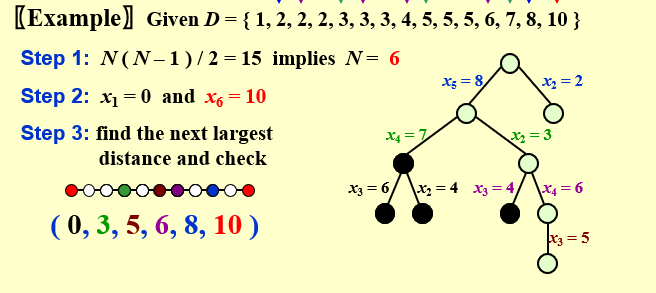
  • 【描述】在一条直线上找到n个地方建立加油站，已知它们两两之间的距离，求出所有加油站的位置，假定第一个加油站的坐标是0

Given N points on the x-axis with coordinates \(x1 < x2 < …< xN\) . Assume that \(x1 = 0\). There are \(N( N – 1 ) / 2\) distances between every pair of points.

  • 【Solution】

    1. 通过n(n-1)/2个距离算出n
    2. 0和最大距离说明都都有加油站
    3. 从D集合中找最大的进行构建,找了就从D中删除距离,失败的话就回到上一种情况.
    4. 每次检验分成靠左边和靠右边两个情况

image-20240401104840497

  1. 首先根据15个距离，算出一共有6个收费站

  2. 计算首尾两个收费站的坐标 \(x1 = 0, x6 = 10\)

  3. find the next largest distance and check

对于长度8，仅可能出现在\(x1\)到\(x5\)或者\(x2\)到\(x6\)

  • \(x5 - x1 = 8\) 说明\(x5 = 8\)
  • \(x6 - x2 = 8\) 说明\(x2 = 2\)

假设我们现在选取\(x5 =8\)， 后续的最大值变为7，仅可能出现在\(x1\)到\(x4\)或者\(x2\)到\(x6\)

  • \(x4 - x1 = 7\) 说明 \(x4 = 7\)
  • \(x6 - x2 = 7\) 说明$ x2 = 3$

假设我们现在选取\(x4 = 7\)，后续的最大值变为6，尽可能出现在\(x1\)到\(x3\)和\(x2\)到\(x6\)

  • \(x3 - x1 = 6\) 说明\(x3 = 6\).但是\(x3\)与\(x4\)距离为1，\(x4\)与\(x5\)距离为1，距离表中没有两个1，矛盾
  • \(x6 - x2 = 6\) 说明$ x2 = 4\(。**但是\)x1\(和\)x2\(距离为4，\)x2\(与\)x5$距离为4，距离表中没有两个4，矛盾**

x4 = 7的道路不同，回溯到x5 = 8， 向下选取另一条道路x2 = 3

后续的最大值变为6，尽可能出现在\(x1\)到\(x4\)和\(x3\)到\(x6\)，得到两个情况\(x4 = 6\)或者\(x3 = 4\)

对于\(x3 = 4\),\(x1\)到\(x3\)的距离，\(x3\)到\(x5\)的距离都是4，矛盾

只剩下\(x4 = 6\)，后续只可能出现 x3 = 5

最终得到结果（0，3，5，6，8，10）

代码实现：

#include<iostream>
#include<vector>
#include<set>

using namespace std;    
#define MAX 200

int Get_num(int n)
{
    for(int i = 1; i <= n; i++)
    {
        if(n == i* (i-1) / 2)
        {
            return i;
        }
    }
    return -1;
}
bool Reconstruct1(vector<int> &path, vector<vector<int>> &solutions, multiset<int> &distances, int n, int left, int right)
{
    // path是存放收费站位置的数组
    // path[1], path[2],...path[left - 1]已知
    // path[right + 1], ... path[n]已知

    bool Found = false;
    // 先判断distances是否为空，为空则找到最后的结果
    if(distances.empty())
    {
        Found = true;
        solutions.push_back(path);
        return Found;
    }
    multiset<int>::iterator iter;
    // 先找到目前distances中的最大值
    int max_distance = *distances.rbegin();
    // 选择一：path[right] = max_distance
    // 此时max_distance 是 收费站 path[0]和path[right]的距离
    path[right] = max_distance;
    int distance;
    // 计算当前right收费站与已知收费站之间的距离
    // 将它们从multiset distances 中删除
    int i;
    for(i = 1; i < left; i++)
    {
        distance = path[right] - path[i];
        iter = distances.find(distance);
        if(iter != distances.end())
        {
            distances.erase(iter);
        }
        else
        {
            // 恢复原状，将已经删除的重新插入
            for(int j = 1; j < i; j++)
            {
                distances.insert(path[right] - path[j]);
            }
            Found = false;
            break;
        }
    }
    if(i == left)
    {
        for(i = right + 1; i <= n; i++)
        {
            distance = path[i] - path[right];
            iter = distances.find(distance);
            if(iter != distances.end())
            {
                distances.erase(iter);
            }
            else
            {
                // 恢复原状，将已经删除的重新插入
                for(int j = 1; j < left; j++)
                {
                    distances.insert(path[right] - path[j]);
                }
                for(int j = right + 1; j < i; j++)
                {
                    distances.insert(path[j] - path[right]);
                }
                Found = false;
                break;
            }
        }
        if(i == n + 1)
        {
            // 进入下一轮的递归
            Found = Reconstruct1(path, solutions, distances, n, left, right - 1);
            if(!Found)
            {
                for(int k = 1; k < left; k++)
                    distances.insert(path[right] - path[k]);
                for(int k = right + 1; k <= n; k++)
                    distances.insert(path[k] - path[right]);
            }
            else
                Found = true;
        }
    }
    if(Found == false)
    {
        // 选择二：path[n] - path[left] = max_distance
        // path[left] = path[n] - max_distance
        path[left] = path[n] - max_distance;
        // 如上删除新的distance
        for(i = 1; i < left; i++)
        {
            iter = distances.find(path[left] - path[i]);
            if(iter != distances.end())
            {
                distances.erase(iter);
            }
            else
            {
                for(int j = 1; j < i; j++)
                {
                    distances.insert(path[left] - path[j]);
                }
                Found = false;
                break;
            }
        }
        if(i == left)
        {
            for(i = right + 1; i <= n; i++)
            {
                iter = distances.find(path[i] - path[left]);
                if(iter != distances.end())
                {
                    distances.erase(iter);
                }
                else
                {
                    for(int j = 1; j < left; j++)
                    {
                        distances.insert(path[left] - path[j]);
                    }
                    for(int j = right + 1; j < i; j++)
                    {
                        distances.insert(path[j] - path[left]);
                    }
                    Found = false;
                    break;
                }
            }
            if(i == n + 1)
            {
                Found = Reconstruct1(path, solutions, distances, n, left + 1, right);
                if(!Found)
                {
                    for(int k = 1; k < left; k++)
                        distances.insert(path[left] - path[k]);
                    for(int k = right + 1; k <= n; k++)
                        distances.insert(path[k] - path[left]);
                }
                else
                    Found = true;
            }
        }
    }

    return Found;
}
bool Reconstruct2(vector<int> &path, vector<vector<int>> &solutions, multiset<int> &distances, int n, int left, int right)
{
// path是存放收费站位置的数组
    // path[1], path[2],...path[left - 1]已知
    // path[right + 1], ... path[n]已知

    bool Found = false;
    // 先判断distances是否为空，为空则找到最后的结果
    if(distances.empty())
    {
        Found = true;
        solutions.push_back(path);
        return Found;
    }
    multiset<int>::iterator iter;
    // 先找到目前distances中的最大值
    int max_distance = *distances.rbegin();
    int i;
    // 选择二：path[n] - path[left] = max_distance
    // path[left] = path[n] - max_distance
    path[left] = path[n] - max_distance;
    // 如上删除新的distance
    for(i = 1; i < left; i++)
    {
        iter = distances.find(path[left] - path[i]);
        if(iter != distances.end())
        {
            distances.erase(iter);
        }
        else
        {
            for(int j = 1; j < i; j++)
            {
                distances.insert(path[left] - path[j]);
            }
            Found = false;
            break;
        }
    }
    if(i == left)
    {
        for(i = right + 1; i <= n; i++)
        {
            iter = distances.find(path[i] - path[left]);
            if(iter != distances.end())
            {
                distances.erase(iter);
            }
            else
            {
                for(int j = 1; j < left; j++)
                {
                    distances.insert(path[left] - path[j]);
                }
                for(int j = right + 1; j < i; j++)
                {
                    distances.insert(path[j] - path[left]);
                }
                Found = false;
                break;
            }
        }
        if(i == n + 1)
        {
            Found = Reconstruct1(path, solutions, distances, n, left + 1, right);
            if(!Found)
            {
                for(int k = 1; k < left; k++)
                    distances.insert(path[left] - path[k]);
                for(int k = right + 1; k <= n; k++)
                    distances.insert(path[k] - path[left]);
            }
            else
                Found = true;
        }
    }

    if(Found == false)
    {
        // 选择一：path[right] = max_distance
        // 此时max_distance 是 收费站 path[0]和path[right]的距离
        path[right] = max_distance;
        int distance;
        // 计算当前right收费站与已知收费站之间的距离
        // 将它们从multiset distances 中删除
        int i;
        for(i = 1; i < left; i++)
        {
            distance = path[right] - path[i];
            iter = distances.find(distance);
            if(iter != distances.end())
            {
                distances.erase(iter);
            }
            else
            {
                // 恢复原状，将已经删除的重新插入
                for(int j = 1; j < i; j++)
                {
                    distances.insert(path[right] - path[j]);
                }
                Found = false;
                break;
            }
        }
        if(i == left)
        {
            for(i = right + 1; i <= n; i++)
            {
                distance = path[i] - path[right];
                iter = distances.find(distance);
                if(iter != distances.end())
                {
                    distances.erase(iter);
                }
                else
                {
                    // 恢复原状，将已经删除的重新插入
                    for(int j = 1; j < left; j++)
                    {
                        distances.insert(path[right] - path[j]);
                    }
                    for(int j = right + 1; j < i; j++)
                    {
                        distances.insert(path[j] - path[right]);
                    }
                    Found = false;
                    break;
                }
            }
            if(i == n + 1)
            {
                // 进入下一轮的递归
                Found = Reconstruct1(path, solutions, distances, n, left, right - 1);
                if(!Found)
                {
                    for(int k = 1; k < left; k++)
                        distances.insert(path[right] - path[k]);
                    for(int k = right + 1; k <= n; k++)
                        distances.insert(path[k] - path[right]);
                }
                else
                    Found = true;
            }
        }
        // 选择二：path[n] - path[left] = max_distance
        // path[left] = path[n] - max_distance
        path[left] = path[n] - max_distance;
        // 如上删除新的distance
        for(i = 1; i < left; i++)
        {
            iter = distances.find(path[left] - path[i]);
            if(iter != distances.end())
            {
                distances.erase(iter);
            }
            else
            {
                for(int j = 1; j < i; j++)
                {
                    distances.insert(path[left] - path[j]);
                }
                Found = false;
                break;
            }
        }
        if(i == left)
        {
            for(i = right + 1; i <= n; i++)
            {
                iter = distances.find(path[i] - path[left]);
                if(iter != distances.end())
                {
                    distances.erase(iter);
                }
                else
                {
                    for(int j = 1; j < left; j++)
                    {
                        distances.insert(path[left] - path[j]);
                    }
                    for(int j = right + 1; j < i; j++)
                    {
                        distances.insert(path[j] - path[left]);
                    }
                    Found = false;
                    break;
                }
            }
            if(i == n + 1)
            {
                Found = Reconstruct1(path, solutions, distances, n, left + 1, right);
                if(!Found)
                {
                    for(int k = 1; k < left; k++)
                        distances.insert(path[left] - path[k]);
                    for(int k = right + 1; k <= n; k++)
                        distances.insert(path[k] - path[left]);
                }
                else
                    Found = true;
            }
        }
    }

    return Found;
}
int main()
{
    int n;
    cin >> n;
    multiset<int> distances1;
    multiset<int> distances2;
    int x;
    for(int i = 0; i < n; i++)
    {
        cin >> x;
        distances1.insert(x);
        distances2.insert(x);
    }
    // 利用distances的数量计算收费站的数量
    int num = Get_num(n);
    vector<int> path1(num + 1, -1);
    vector<int> path2(num + 1, -1);
    vector<vector<int>> solutions;
    path1[1] = 0;
    path1[num] = *distances1.rbegin();
    path2[1] = 0;
    path2[num] = *distances2.rbegin();
    distances1.erase(path1[num]);
    distances2.erase(path2[num]);
    Reconstruct1(path1, solutions, distances1, num, 2, num - 1);
    Reconstruct2(path2, solutions, distances2, num, 2, num - 1);
    for(int i = 0; i < solutions.size(); i++)
    {
        for(int j = 1; j <= num; j++)
        {
            cout << solutions[i][j] << " ";
        }
        cout << endl;
    }
    cout << "Total number of solutions : " << solutions.size() << endl;

}

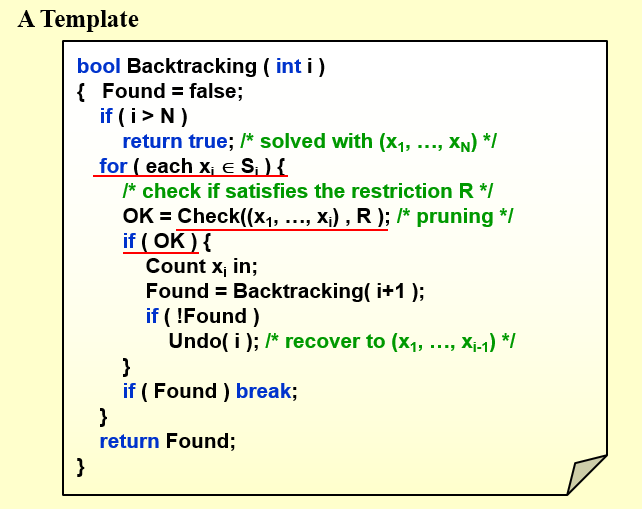
回溯算法的模板

image-20240401112000643

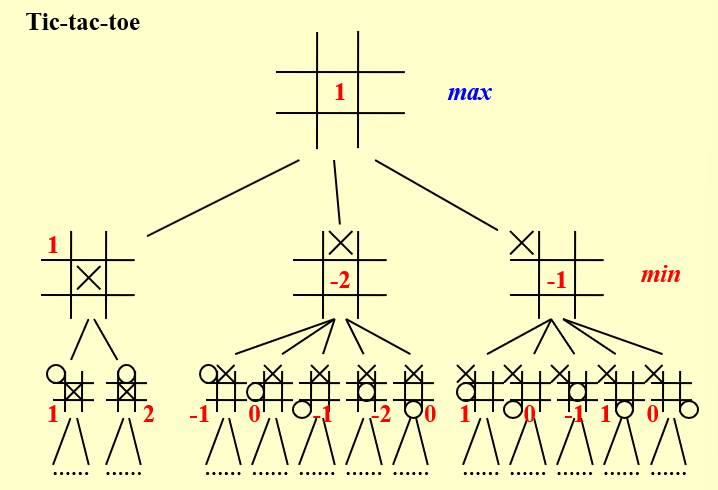
6.3 井字棋

  • AI下棋问题:需要推算出所有可能的情况并且选择当前胜率最高的情况往下走

  • MinMax Strategy问题(最大最小策略):

  • goodness函数\((f(P)=W_{AI}-W_{Human})\)，W是当前情况下某一方可能赢的所有结果，不需要考虑另一方后面会怎么下，只要计算自己在当前局势下的任何可以赢的方法.

  • The human is trying to minimize the value of the position P, while the computer is trying to maximize it.

image-20240401114922424

X表示机器下的位置， O表示人下的位置

最开始模拟最初的两步，AI先手，选择对自己最有利，也就是max的情况

机器会最大化\(f(P)\),所以第一轮机器会下在中心点

第二轮，人为了最小化\(f(P)\),将下在角落

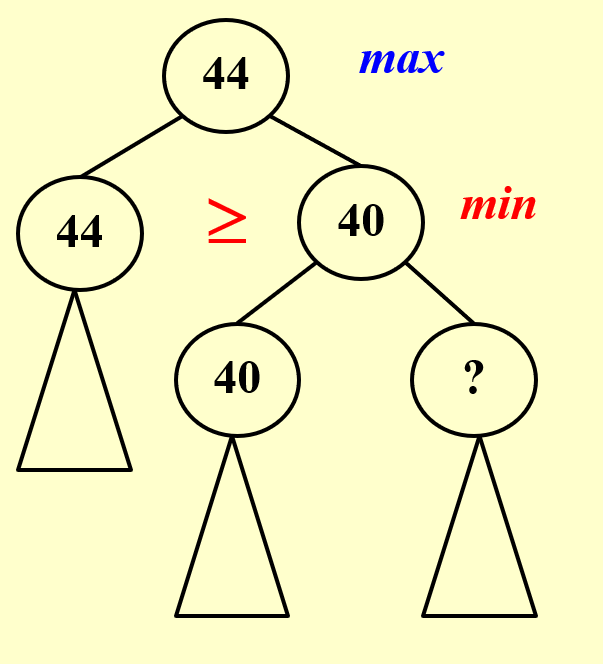
6.4 \(\alpha \beta\)剪枝搜索

image-20240401115736937

AI在max处的选择，不需要考虑问号处的value。

因为 min层会选择小于等于的数作为结果，max必然会选择大于等于44的结果，也就没必要计算问号了

image-20240401115954131

6.5 习题集

  1. In the 4-queens problem,$ (x1, x2, x3, x4)$ correspond to the 4 queens’ column indices. During backtracking, (1, 3, 4, ?) will be checked before (1, 4, 2, ?), and none of them has any solution in their branches.

    T

    首先检查1，3，4，发现不满足。然后检查1，4，开头的1，2，3，4，5，6…。首先从第一行往下检查，从左往右遍历。如果不满足，不进行下一行的检查。

  1. In a Turnpike Reconstruction Problem, given distance set \(D = { 2, 2, 4, 4, 6, 8 }\),$ x1~x4 = ( 0, 2, 4, 8 )$ is the only solution provided that \(x1 = 0.\) 0，4，6，8也是可以的。按照那个算法：首先\(x4=8\)

    然后找出D最大的为6，尝试\(x3=6\)，发现8-6在D中。将2从D中删除

    然后找D最大的为4，尝试\(x2=4\)，发现8-4=4，6-4=2在D中，将2,4删除。

    最后D为空，说明解决问题。

    有一种解法，根据镜像就存在第二种解法

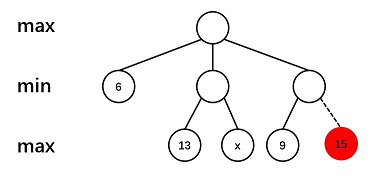
  2. Given the following game tree, the red node will be pruned with α-β pruning algorithm if and only if __.

    img

    剪枝发生的情况：其兄弟节点比它的节点更优。它的另外一个子节点被剪枝。

    此时，min选择了9，则为了比9更优，x必须大于9，才能使得中间一个节点无论如何大于9，则Max不会选择最右边节点。D

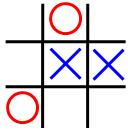
  3. In the Tic-tac-toe game, a "goodness" function of a position is defined as \(f(P) = W_{computer} - W_{human}\)where \(W\) is the number of potential wins at position \(P\).In the following figure, O represents the computer and X the human. What is the goodness of the position of the figure?

    • A. -1

    • B. 0

    • C. 4

    • D. 5

    X可以单走一步就是赢，X走两步赢的方法有两种

    O走两步赢的方法有3种

    3 - 3 = 0

  4. Given the following game tree, which node is the first one to be pruned with α-β pruning algorithm?

    abtree1.png

    • A. a

    • B. b

    • C. c

    • D. d

    搜索到 b 等于 86 时，a处的值会大于86，而min层会选择小于等于68的结点，所以c点不需要再检测。

    即 β 剪枝。

    image-20240401115736937

    image-20240401115954131