7. Divide & Conquer¶
约 3636 个字 7 行代码 预计阅读时间 18 分钟
7.1 概述¶
套用 Wiki 上的说法,分治法(Divide-and-conquer algorithm)属于一种算法范型,它的基本思想是将一个问题分解为若干个规模较小的相同问题,然后递归地解决这些子问题,最后将这些子问题的解合并得到原问题的解,一个比较经典的案例就是归并排序。
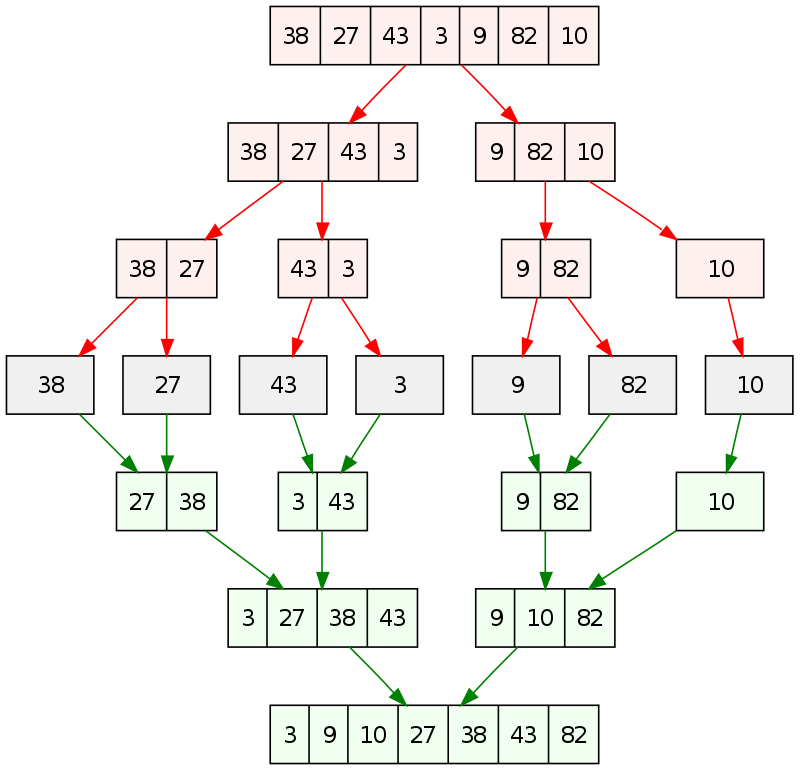
归并排序可以说是分治法最经典的体现:对于一个未排序的有n个元素的序列,不断地将它从中间分开为两个子序列,最终形成n个分别只有1个元素的子序列。只有1个元素的子序列自然是有序的,然后再将它们两两合并起来,并在合并过程中将子序列排序,最终返回的n个元素的合并序列即为有序。其过程如下图所示。
void merge_sort(vector<T> a, int front, int end) {
if (front >= end) return;
int mid = front + (end - front) / 2;
merge_sort(a, front, mid);
merge_sort(a, mid + 1, end);
merge(a, front, mid, end);
}
7.2 Closet Points Problem¶
二维最近点问题(Closet Points Problem),指的是给定平面上的 n 个点,找出其中距离最近的两个点。
7.2.1 朴素方法¶
最朴素的做法当然是枚举所有的点对,一共需要 \(C_{N}^{2} = {{N}\choose{2}} = \frac{N(N-1)}{2}\) 即复杂度为 \(O(N^2)\)。
7.2.2 分治方法¶
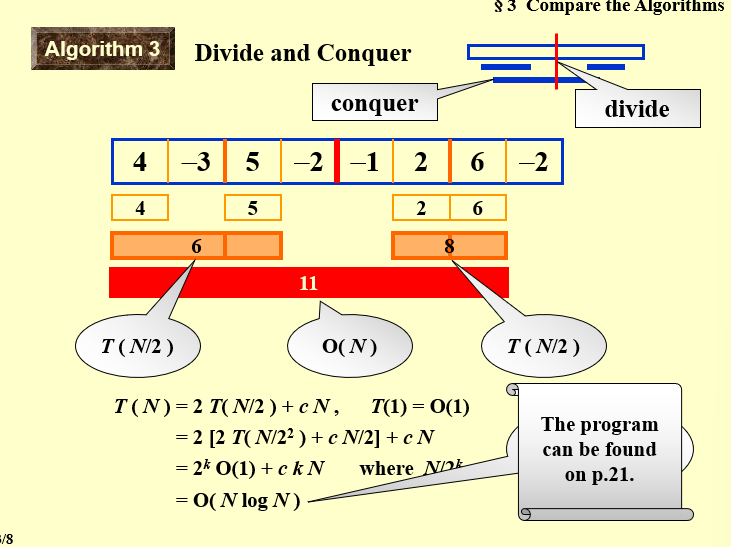
现在我们类比最大子序列和问题的分治做法。
最大子序列和的分治做法"
将序列分为左右两部分,分别求解最大子序列和;
求解跨越中点的最大子序列和;比较三者的大小,取最大值;
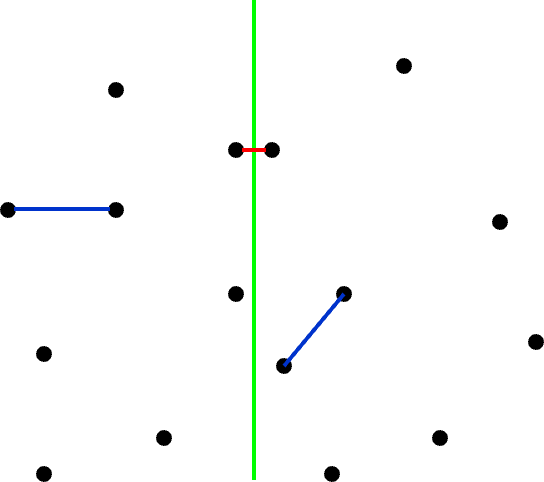
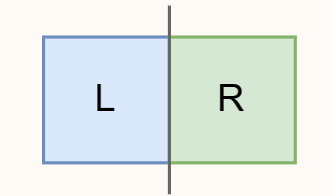
我们可以将整个平面分为两个部分,即如图中绿色线将点对划分为两个部分。
为解决二维最近点问题,我们同样分为这么三步:
- 将点对分为左右两部分,分别求解最近点对;
寻找跨越分界线的点对,从中寻找最近点对;- 比较三者的大小,取最小值;
-
先计算左右两部分最近点对的距离,进行比较后,选择最小距离中较小的为\(\delta\)
-
接下来我们仅需要寻找跨越分界线的点对中最小距离小于\(\delta\)的部分。
-
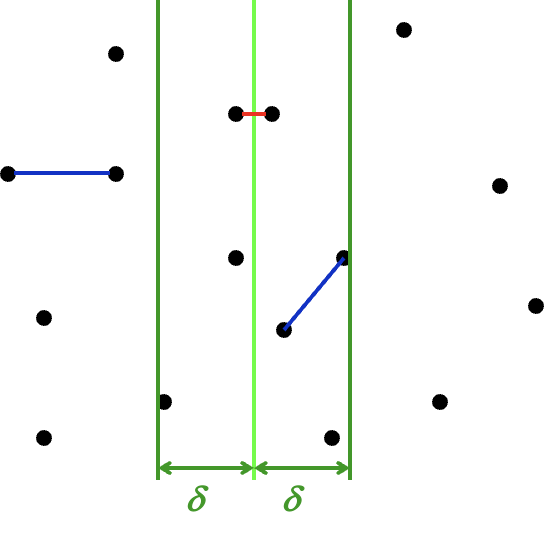
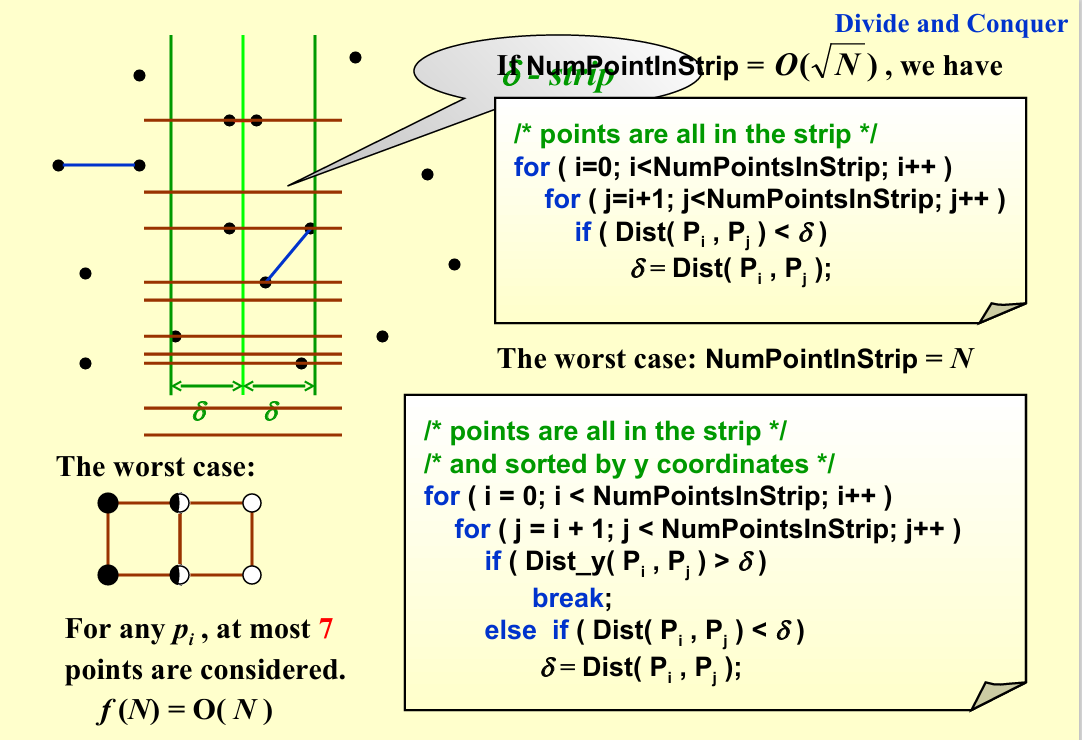
为了减少步骤二的计算量,我们需要pass掉一些显然是不可能的点对。步骤二中被拿出的点,一定一个在分界点左侧,一个在分界点右侧,对于距离分界线\(\delta\)以外的点,不可能形成最小距离小于\(\delta\)(
水平距离就大于δ)。所以我们仅考虑距离分界线\(\delta\)以内的点。如图,现在我们知道,只有落在两条深绿色之间的点才可能会更新答案。
-
刚刚是对x轴上的距离进行限制,同理我们也可以在y轴上对距离进行限制
对于选定点 \(p_{l_i}\),其所有可能导致答案更新的点都被框定在一个 \(2\delta \times \delta\) 的矩形中。
为什么y方向上限制仅仅是δ呢?因为我们仅考虑当前所在的点,与上面的点的距离,这样切换到下方的点时候,不会与上方的点造成最小距离的重复计算,可以有效的防止点对的重复 -
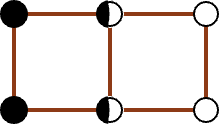
在这样一个区域中,我们需要约束所有落在 \(\delta \times \delta\) 的 L 区域中的点,互相的距离都大于等于 \(\delta\),对 R 区域中的点也有相同的约束。
也就是说,一旦在左侧选中一个点(不在边界)后,在 δ x δ 的 L 区域中,左侧范围内不会出现第二个点,因为左边点对的最小距离就是δ对于在边界上的点,显然位于四个角的情况,需要计算的次数最多,对应worse case,最正常的case 就是左右各一个点worse case 对应在最理想最理想的情况下——闭区间、允许点重合的情况下,这个矩形最多也只能放八个点(两边各四个):本质上是六个点(去重)
-
于是我们能够得到结论,对于每一个选定的 \(p_{l_i}\),寻找其可能导致答案更新的点的复杂度都是常数级的。
而枚举这些“选定点”,也就是枚举 \(p_{l_i}\),其复杂度(撑死)是 \(O(N)\)。
于是我们能得到这个分治的时间复杂度计算递推公式:
-
7.3 复杂度分析¶
在开始接下来的内容之前,我们需要给出更一般的,我们想要解决的问题,即求解时间复杂度递推公式形如下式的算法的时间复杂度:
例如,上面的最近点对问题,就是 \(a = 2,\; b = 2,\; f(N) = O(N)\) 的情况。
7.3.1 代换法¶
代换法(substitution method)的思路非常直白,首先我们通过某些手段(比如大眼观察法👀)来得到一个预设的结果,接下来通过代入、归纳的方法来证明这个结果。
求解复杂度: $$ T(N) = 2\; T(\frac{N}{2}) + N $$ guess: $$ T(N) = O(N\log N) $$
代入:
- 利用\(T(N) = O(NlogN)\),对于足够小的 \(m < N\),有:
- 将上式代入:
- 得:
对于足够小的 \(m = 2\) 式子就可以成立,由归纳法得结论成立。
7.3.2 递归树法¶
递归树法(recursion-tree method)的思路是,我们通过画出递归树来分析算法的时间复杂度, $$ a^{\log_b N} = \exp^{\frac{\ln N}{\ln b} \ln a} = \exp^{\frac{\ln a}{\ln b} \ln N} = N^{\log_b a} $$ 对于一个递推式,我们将它不断展开以后,其形式大概会是这样:
其中,由于末端子问题的规模一般都足够小,可以认为 \(T(N_{leaf_i})\) 都是常数,于是上式又可以变化为:
具体来说解释其含义,combine 部分就是在每一次“分治”的处理时间,如合并当前的子问题分治后的结果,体现在递推式的 \(f(N)\) 部分;而 conquer 部分指的是当“分治”的“治”在“分”的末端的体现,即对于足够小的规模的问题,不再需要继续“分”的时候,对其处理的开销。
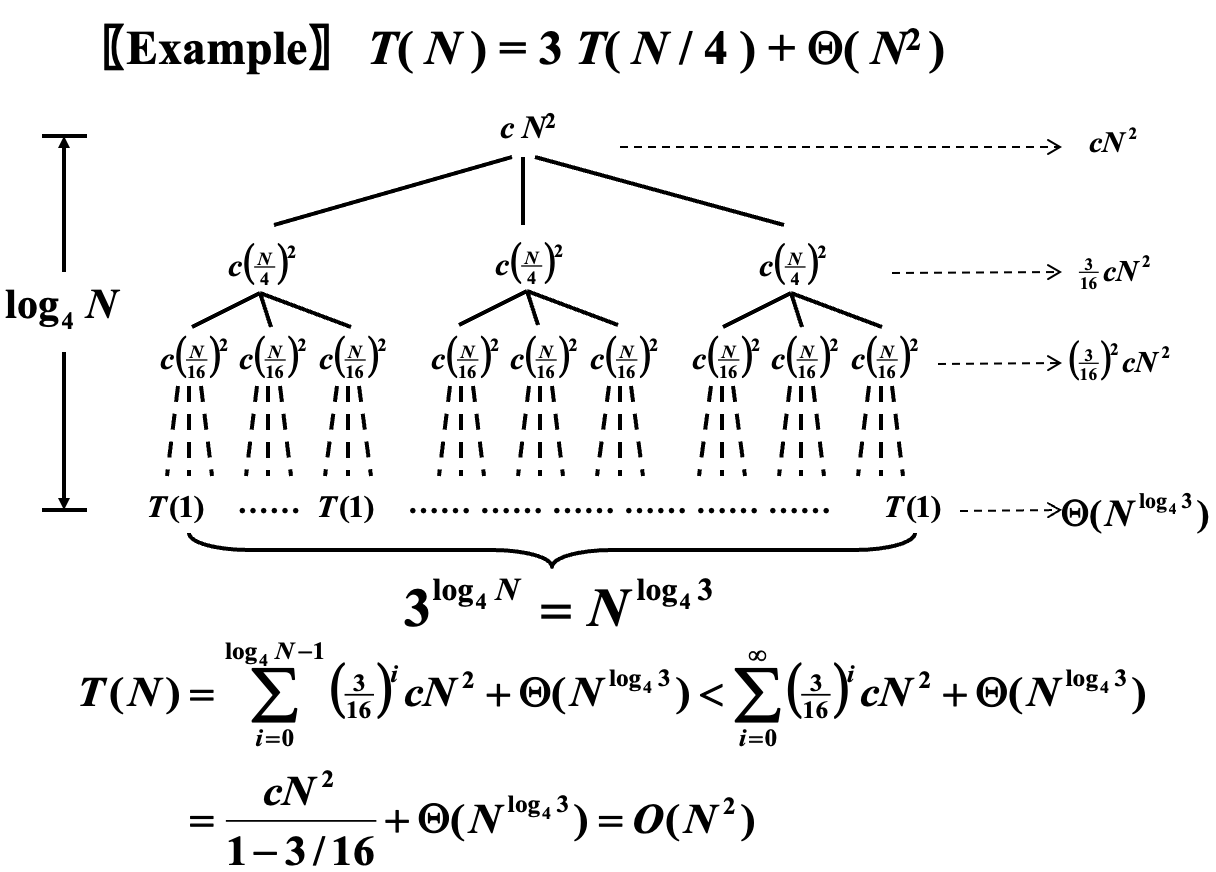
可以发现,此情况下 \(a = 3,\; b = 4,\; f(N) = \Theta(N^2)\),也就是说每次分为 \(3\) 个子问题,子问题的规模是 \(\frac{N}{4}\),而合并开销为 \(\Theta(N^2)\)。
此时由于分治的策略是相对均匀的,所以我们可以认为得到的是一个完美三叉树(full binary tree)。
显然,树高为 \(\log_4 N\),根记为 \(0\),每个分治节点的 combine 开销已经标注在图的节点位置,横向箭头标记的是对该层所有节点的开销的求和。
当前情况下,第0层对应的结点数是1,第1层对应的结点数3,第2层对应的结点数为\(3^2 = 9\),依次类推,第i层的结点数\(3^i\)
第0层的结点合并开销为\(cN^2\), 第1层的结点合并开销为\(c(\dfrac{N}{4})^2\),依次类推第i层的合并开销为\(c(\dfrac{N}{4^i})^2\)
将所有的合并开销和最后一层的常数开销计算在一起
7.3.3 主方法¶
主方法(master method)之所以叫“主”,是因为它分析的是 combine 和 conquer 部分孰为主导。
形式一¶
definition "Form 1"
对于形如 \(T(N)=aT(N/b)+f(N)\) 的递推式,其中\(a>=1, b>1\):
- 若 \(f(N)=O(N^{(\log_b{a})-\varepsilon}), \text{ for }\varepsilon>0\),那么 \(T(N)=\Theta(N^{\log_b{a}})\);
- 若 \(f(N)=\Theta(N^{\log_b{a}})\),那么 \(T(N)=\Theta(N^{\log_b{a}}\log{N})\);
- 若 \(f(N)=\Omega(N^{(\log_b{a})+\varepsilon}), \text{ for }\varepsilon>0\) 且 \(af(\frac{N}{b})<cf(N), \text{ for } c<1 \text{ and } \forall N > N_0\),那么 \(T(N)=\Theta(f(N))\);
情况三的后面那个条件又叫 regularity condition。
回顾我们在前面说的那句话,主方法(master method)之所以叫“主”,是因为它分析的是 combine 和 conquer 部分孰为主导,观察三种情况的区分条件都是比较 \(f(N)\)(每一次的 combine 开销) 和 \(N^{\log_b{a}}\)(即求和式中的 conquer 的开销).
为什么要比较这两个呢?且看递推树得到的结论,分为所有的叶子结点的常数开销和非叶子结点的合并开销,分别对应 cf(N) 和 N^{log_b a},观察比较得出哪一个占主导
当 \(f(N)\) 足够小时,以 conquer 开销为主(i.e. case 1);当足够大时,以 combine 为主(i.e. case 3);而其中还有一个中间状态(i.e. case 2)。
- 【eg1】\(a = b = 2,\; f(N) = N\)
- \(f(N) = N = \Theta(N^{\log_2{2}})\),适用于情况 2
- 因此得到结果 \(T(N) = \Theta(N \log N)\)
- 【eg2】\(a = b = 2,\; f(N) = N \log N\)
- \(f(N) = N \log N\),虽然 \(N \log N = \Omega(N^{\log_2{2}})\),但是 \(N \log N \neq \Omega(N^{(\log_2{2}) + \varepsilon})\),所以不适用于情况 3;
虽然你的f(N)比N^{log_b a}要大,但是达不到 $N \log N \neq \Omega(N^{(\log_2{2}) + \varepsilon})$。所以不满足条件- 具体来说,\(\lim \limits_{N\to \infty} \frac{N \log N}{N^{1+\varepsilon}}=\lim \limits_{N\to \infty} \frac{\log N}{N^{\varepsilon}} = 0 \text{ for fixed } \varepsilon > 0\); 出了 \(\varepsilon\) 的一定作用;
证明¶
proof "proof for form 1"
对于形如 \(T(N)=aT(N/b)+f(N)\) 的递推式,我们需要依次证明,此处我们使用递归树法进行证明。
section "情况一"
🎯 目标:若 \(f(N)=O(N^{(\log_b{a})-\varepsilon}), \text{ for }\varepsilon>0\),那么 \(T(N)=\Theta(N^{\log_b{a}})\);
🪧 证明:我们首先需要绘制出对应的递归树,或者搞清楚展开后的情况,因为懒得画图所以我这里采用文字叙述。
树高 \(\log_b{N}\),共 \(\log_b{N} + 1\) 层,则有:
- 第 \(0\) 层(根)一共 \(1\) 项,combine 的开销为 \(f(N)\);
- 第 \(1\) 层一共 \(a\) 项,combine 的开销为 \(a\times f(\frac{N}{b})\);
- 第 \(2\) 层一共 \(a^2\) 项,combine 的开销为 \(a^2 \times f(\frac{N}{b^2})\);
- ......
- 第 \(j\) 层一共 \(a^j\) 项,combine 的开销为 \(a^j \times f(\frac{N}{b^j})\);
- ......
- 第 \((\log_b{N}) - 1\) 层一共 \(a^{(\log_b{N}) - 1}\) 项,combine 的开销为 \(a^{(\log_b{N}) - 1} \times f(\frac{N}{b^{(\log_b{N}) - 1}})\);
- 第 \(\log_b{N}\) 层,即为叶子层,一共 \(a^{\log_b{N}} = N^{\log_b{a}}\) 项,conquer 的开销为 \(N^{\log_b{a}} \times \Theta(1) = \Theta(N^{\log_b{a}})\);
得到求和式:
而我们有条件 \(f(N)=O(N^{(\log_b{a})-\varepsilon}), \text{ for }\varepsilon>0\),将它代入到上式中得到:
至此,情况一证明完毕。
section "情况二"
🎯 目标:若 \(f(N)=\Theta(N^{\log_b{a}})\),那么 \(T(N)=\Theta(N^{\log_b{a}}\log{N})\);
🪧 证明:前面的部分和情况一的类似,我们通过相同的步骤得到相同的求和式:
而我们有条件 \(f(N)=\Theta(N^{\log_b{a}})\),将它代入到上式中得到:
至此,情况二证明完毕。
section "情况三"
🎯 目标:若 \(f(N)=\Omega(N^{(\log_b{a})+\varepsilon}), \text{ for }\varepsilon>0\) 且 \(af(\frac{N}{b})<cf(N), \text{ for } c<1 \text{ and } \forall N > N_0\),那么 \(T(N)=\Theta(f(N))\);
🪧 证明:情况三的证明,从条件的变化就可以看出来和前面稍许有些不同了。不过求和式的得到还是一样,通过和之前一样的方法,我们首先得到求和式:
接下来的步骤和之前不同。在继续之前,我们首先观察不等式 \(af(\frac{N}{b})<cf(N)\),在我们的求和式中,我们观察到我们有大量的形如 \(a^jf(\frac{N}{b^j})\) 的项,而这些项都可以通过迭代上面那个不等式来实现,即:
将这个不等式应用于求和式中,我们能够得到:
而由于 \(c<1\),所以 \(\log_b{c} < 0\);而 \(N > 0\),而且一般非常大,所以 \(N^{\log_b{c}} \in (0,1)\)。因此,对于确定的常数 \(c\),我们有 \(\frac{1-N^{\log_b{c}}}{1-c} \in \left(0, \frac{1}{1-c}\right)\);
因此,上式便能改变为:
并且,由于 \(f(N)=\Omega(N^{(\log_b{a})+\varepsilon}), \text{ for }\varepsilon>0\),所以根据符号定义可以得到 \(T(N) = O(f(N))\)。
而我们知道,要证明 \(T(N) = \Theta(f(N))\) 还需要证明 \(T(N) = \Omega(f(N))\):
由此得到 \(T(N) = \Omega(f(N))\),最终证得 \(T(N) = \Theta(f(N))\),至此,情况三证明完毕。
形式二¶
definition "Form 2"
对于形如 \(T(N) = aT(\frac{N}{b}) + f(N)\) 的递推式:
- 若 \(af(\frac{N}{b}) = \kappa f(N) \text{ for fixed } \kappa < 1\),那么 \(T(N) = \Theta(f(N))\);
- 若 \(af(\frac{N}{b}) = \Kappa f(N) \text{ for fixed } \Kappa > 1\),那么 \(T(N) = \Theta(N^{\log_b{a}}) = \Theta(a^{\log_b{N}})\)(个人感觉后面那个式子更方便直观记忆);
- 若 \(af(\frac{N}{b}) = f(N)\),那么 \(T(N) = \Theta(f(N) \log_b N)\);
证明¶
proof "proof for form 2"
对于形如 \(T(N)=aT(N/b)+f(N)\) 的递推式,基于线性关系的形式二的证明实际上和形式一的第三种情况的证明非常相像。
假设我们有 \(af(\frac{N}{b}) = c f(N)\),只需要讨论 \(c\) 的取值范围对结果的影响,就可以一次性得到结果。
类似于形式一的第三种情况的证明,我们迭代该关系式,得到关系:
于是,我们有:
接下来,又回到了f(N)与N^{log_b a}比大小的环节,但是我们只有\(af(\frac{N}{b}) = c f(N)\)
$$
c f(N) \sim a f(\frac{N}{b}) \sim ... \sim a^L f(\frac{N}{b^L})
$$
我们假设 \(\frac{N}{b^L}\) 足够小(即递归到最末端,只需要进行 conquer 的时候),即 \(\frac{N}{b^L} = \Theta(1)\),那么就有 \(L = \Theta(\log_b{N})\)。于是,我们有:
- 当 \(c < 1\) 时,实际上有 \(f(N) > af(\frac{N}{b})\);对应的\(f(N) > N^{log _b a}\)
- 当 \(c = 1\) 时,实际上有 \(f(N) = af(\frac{N}{b})\);对应的\(f(N) = N^{log _b a}\)
- \(c > 1\) 时,实际上有 \(f(N) < af(\frac{N}{b})\);对应的\(f(N) < N^{log _b a}\)
形式三¶
definition "Form 3"
第三种形式是对于 \((N)\) 的特别形式,当递推关系满足:\
其复杂度有结论:
实际上这个式子也非常好认,属于形式二的一种特殊形式。可以对照着看,非常容易看出关系。
依然采用递推树的方法
第 i 层,结点数 \(a ^ i\), 每个结点的合并开销 \(\Theta ((\dfrac{N}{b^i})^klog^p \frac{N}{b^i}\)
- 当 \(a > b^k\)时,\(N^{log_ba} > N^k\),显然是后面大
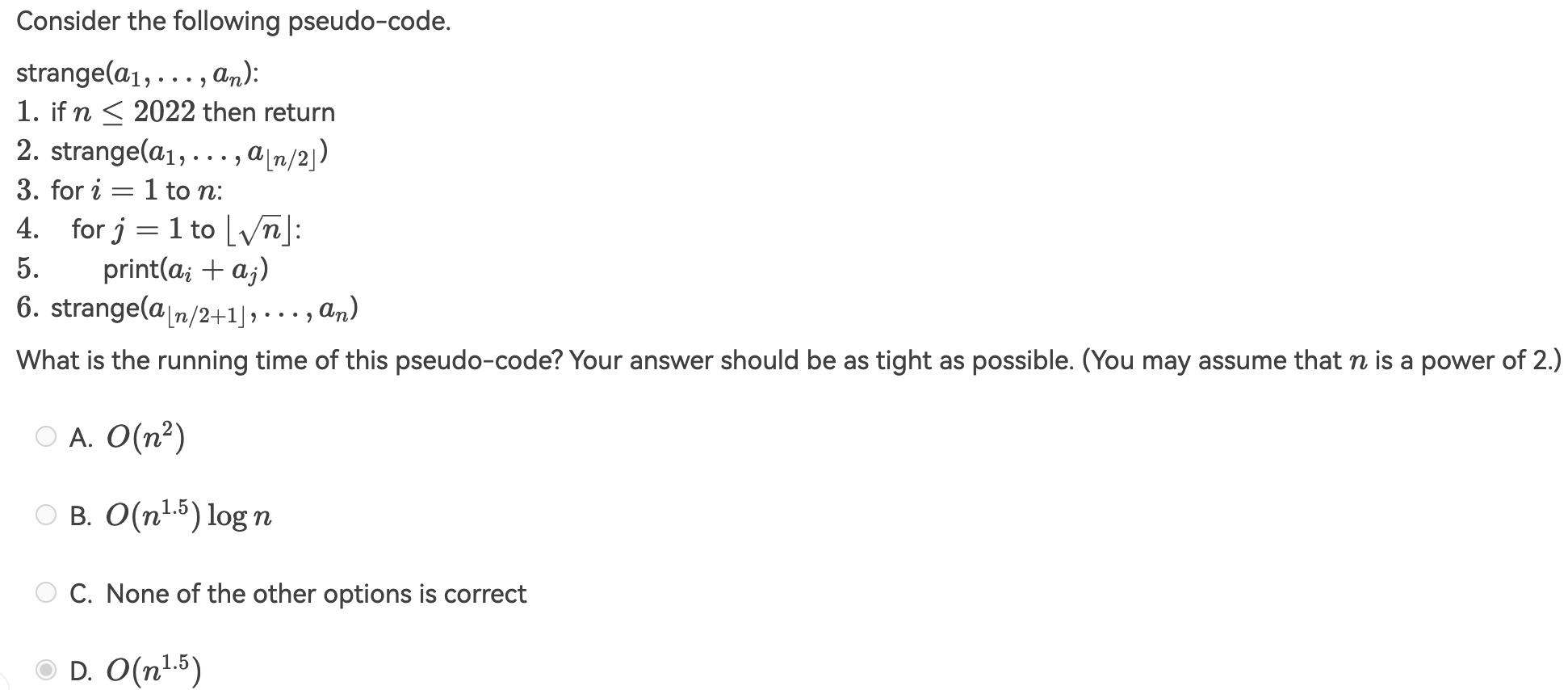
7.4 习题¶
-
\(T(N) = 2T(\sqrt N) + log N\) Which one of the following is the lowest upper bound of \(T(n)\) for the following recursion \(T(n) = 2T(\sqrt{n}) + \log n\)?
-
A. \(O(\log n\log \log n)\)
-
B. \(O(\log^2 n)\)
-
C. \(O(n\log n)\)
-
D. \(O(n^2)\)
- 先采用还原法,令\(m = log N\), 那么原式转化为\(T(2^m) = 2(T^{m/2})+m\)
- 再使用换元法,令\(S(m) = T(2^m)\),那么原式转化为\(S(m) = 2S(m/2) + m\)
发现这就是递归排序的时间复杂度,得到\(S(m) = mlogm\)- 还原,令\(2^m = N\),则 \(m = log N\),最终\(T(N) = S(m) = logN log(logN)\)
-
-
When solving a problem with input size \(N\) by divide and conquer, if at each stage the problem is divided into 8 sub-problems of equal size \(N/3\), and the conquer step takes \(O(N^2 logN)\) to form the solution from the sub-solutions, then the overall time complexity is __.
-
A. \(O(N^2 logN)\)
-
B. \(O(N^2 log^2 N)\)
-
C. \(O(N^3 logN)\)
-
D. \(O(N^{log8/log3})\)
运用形式三,a = 8, b = 3, p = 1, k = 2, a < b ^ k最终答案是A
-
-
To solve a problem with input size \(N\) by divide and conquer algorithm, among the following methods, __ is the worst.
-
A. divide into 2 sub-problems of equal complexity \(N/3\) and conquer in \(O(N)\)
-
B. divide into 2 sub-problems of equal complexity \(N/3\) and conquer in \(O(NlogN)\)
-
C. divide into 3 sub-problems of equal complexity \(N/2\) and conquer in \(O(N)\)
-
D. divide into 3 sub-problems of equal complexity \(N/3\) and conquer in \(O(NlogN)\)
A. \(T(N) = 2T(N/3) + O(N), N^{log_3 2} < N\),最终时间复杂度为\(T(N) = O(N)\)
B.\(T(N) = 2T(N/3) + O(NlogN),a = 2, b= 3, k = 1, p =1, a < b^k\),最终时间复杂度为\(T(N) = O(NlogN)\)
C.\(T(N) = 3T(N/2)+O(N), N^{log_2 3 > N}\)最终时间复杂度为\(T=O(N^{log_2 3)}\)
D.\(T(N) = 3(T/3) + O(NlogN), a = 3, b= 3, k =1, p= 1, a = b^k\),最终时间复杂度为\(T=O(Nlog^2N)\)
-
-
3-way-mergesort : Suppose instead of dividing in two halves at each step of the mergesort, we divide into three one thirds, sort each part, and finally combine all of them using a three-way-merge. What is the overall time complexity of this algorithm ?
-
A. \(O(n(\log^2 n))\)
-
B. \(O(n^2 \log n)\)
-
C. \(O(n\log n)\)
-
D. \(O(n)\)
\(T(N) = 3T(N/3)+O(N), N^{log_3 3} = N\),最终时间复杂度为\(O(NlogN)\)
-