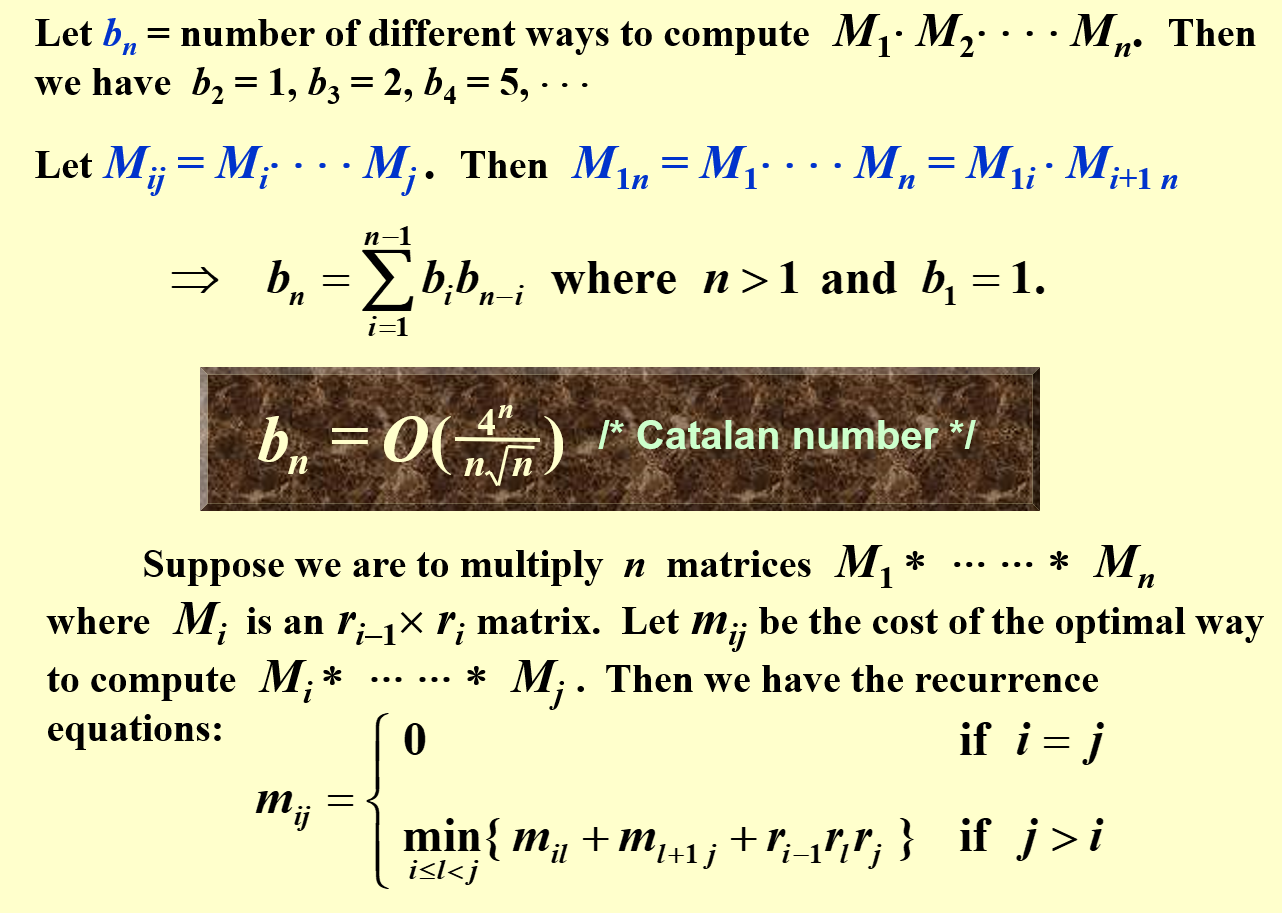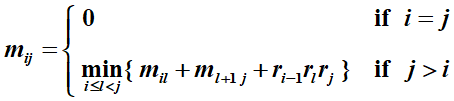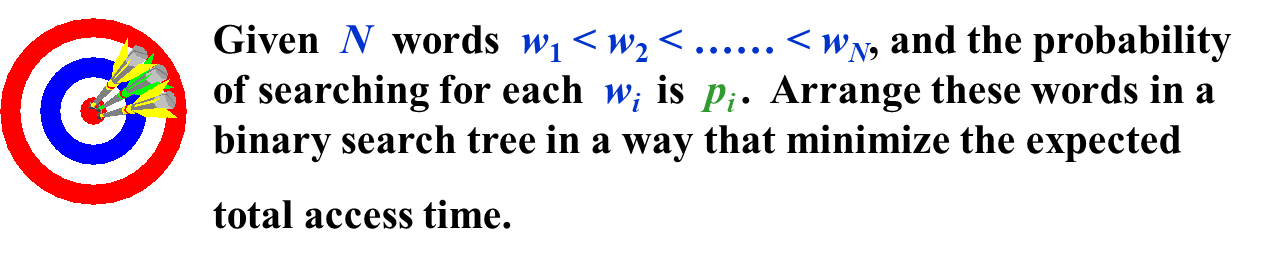跳转至

8. Dynamic Programming

约 3231 个字 149 行代码 预计阅读时间 18 分钟

7.1. 动态规划简介

  1. 动态规划的定义

    动态规划（Dynamic Programming）：简称 DP，是一种求解多阶段决策过程最优化问题的方法。在动态规划中，通过把原问题分解为相对简单的子问题，先求解子问题，再由子问题的解而得到原问题的解。

  2. 动态规划的核心思想

    动态规划的核心思想：

    1. 把「原问题」分解为「若干个重叠的子问题」，每个子问题的求解过程都构成一个 「阶段」。在完成一个阶段的计算之后，动态规划方法才会执行下一个阶段的计算。
    2. 在求解子问题的过程中，按照「自顶向下的记忆化搜索方法」或者「自底向上的递推方法」求解出「子问题的解」，把结果存储在表格中，当需要再次求解此子问题时，直接从表格中查询该子问题的解，从而避免了大量的重复计算。

    这看起来很像是分治算法，但动态规划与分治算法的不同点在于：

    1. 适用于动态规划求解的问题，在分解之后得到的子问题往往是相互联系的，会出现若干个重叠子问题。
    2. 使用动态规划方法会将这些重叠子问题的解保存到表格里，供随后的计算查询使用，从而避免大量的重复计算。

  3. 动态规划的简单例子

    斐波那契数列：数列由 \(f(0) = 1，f(1) = 2\) 开始，后面的每一项数字都是前面两项数字的和。

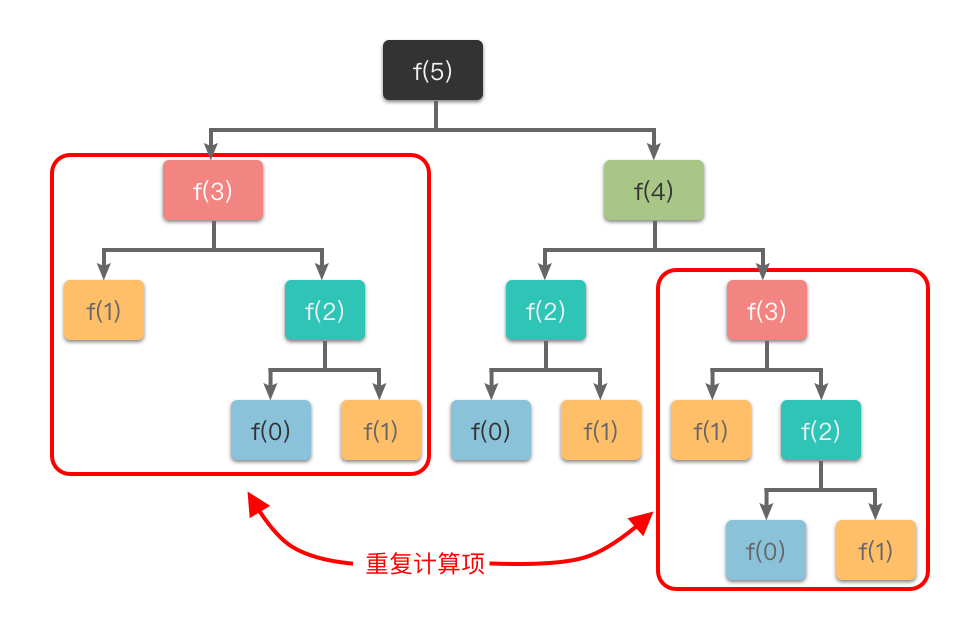
    通过公式 \(f(n) = f(n - 2) + f(n - 1)\)，我们可以将原问题 \(f(n)\) 递归地划分为 \(f(n - 2)\) 和 \(f(n - 1)\) 这两个子问题。其对应的递归过程如下图所示：

    img

    从图中可以看出：如果使用传统递归算法计算 \(f(5)\)，需要先计算 \(f(3)\) 和 \(f(4)\)，而在计算 \(f(4)\) 时还需要计算 \(f(3)\)，这样 \(f(3)\) 就进行了多次计算。同理 \(f(0)\)、\(f(1)\)、\(f(2)\) 都进行了多次计算，从而导致了重复计算问题。

    为了避免重复计算，我们可以使用动态规划中的「表格处理方法」来处理。

    这里我们使用「自底向上的递推方法」求解出子问题 \(f(n - 2)\) 和 \(f(n - 1)\) 的解，然后把结果存储在表格中，供随后的计算查询使用。具体过程如下：

    1. 定义一个数组 \(dp\)，用于记录斐波那契数列中的值。
    2. 初始化 \(dp[0] = 0，dp[1] = 1\)。
    3. 根据斐波那契数列的递推公式 \(f(n) = f(n - 1) + f(n - 2)\)，从 \(dp(2)\) 开始递推计算斐波那契数列的每个数，直到计算出 \(dp(n)\)。
    4. 最后返回 \(dp(n)\) 即可得到第 \(n\) 项斐波那契数。

    具体代码如下：

    int Fibonacci(int N)
{
    int i, Last, NextToLast, Answer;
    if (N <= 1)
        return 1;
    Last = NextToLast = 1;
    /* F(0) = F(1) = 1 */
    for (i = 2; i <= N; i++)
    {
        Answer = Last + NextToLast;
        /* F(i) = F(i-1) + F(i-2) */
        NextToLast = Last;
        Last = Answer;
        /* update F(i-1) and F(i-2) */
    } /* end-for */
    return Answer;
}

    这种使用缓存（哈希表、集合或数组）保存计算结果，从而避免子问题重复计算的方法，就是「动态规划算法」。

7.2. 动态规划的特征

究竟什么样的问题才可以使用动态规划算法解决呢？

首先，能够使用动态规划方法解决的问题必须满足以下三个特征：

  1. 最优子结构性质
  2. 重叠子问题性质
  3. 无后效性

7.2.1 最优子结构性质

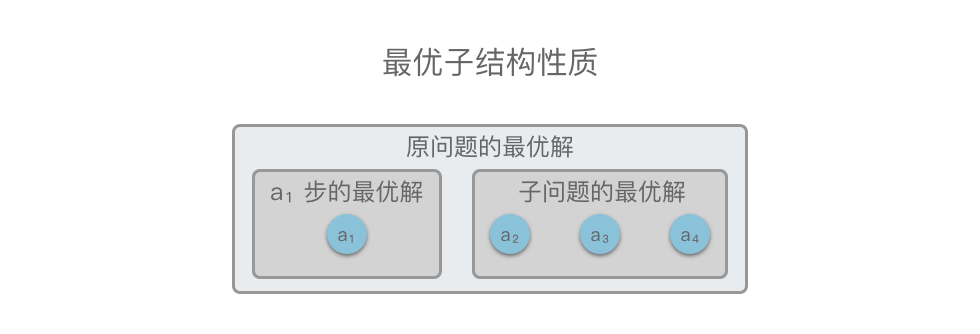
最优子结构：指的是一个问题的最优解包含其子问题的最优解。

举个例子，如下图所示，原问题 \(S = \lbrace a_1, a_2, a_3, a_4 \rbrace\)，在 \(a_1\) 步我们选出一个当前最优解之后，问题就转换为求解子问题 \(S*{子问题} = \lbrace a_2, a_3, a_4 \rbrace\)。如果原问题 \(S\) 的最优解可以由「第 \(a_1\) 步得到的局部最优解」和「 \(S*{子问题}\) 的最优解」构成，则说明该问题满足最优子结构性质。

也就是说，如果原问题的最优解包含子问题的最优解，则说明该问题满足最优子结构性质。

img

7.2.2 重叠子问题性质

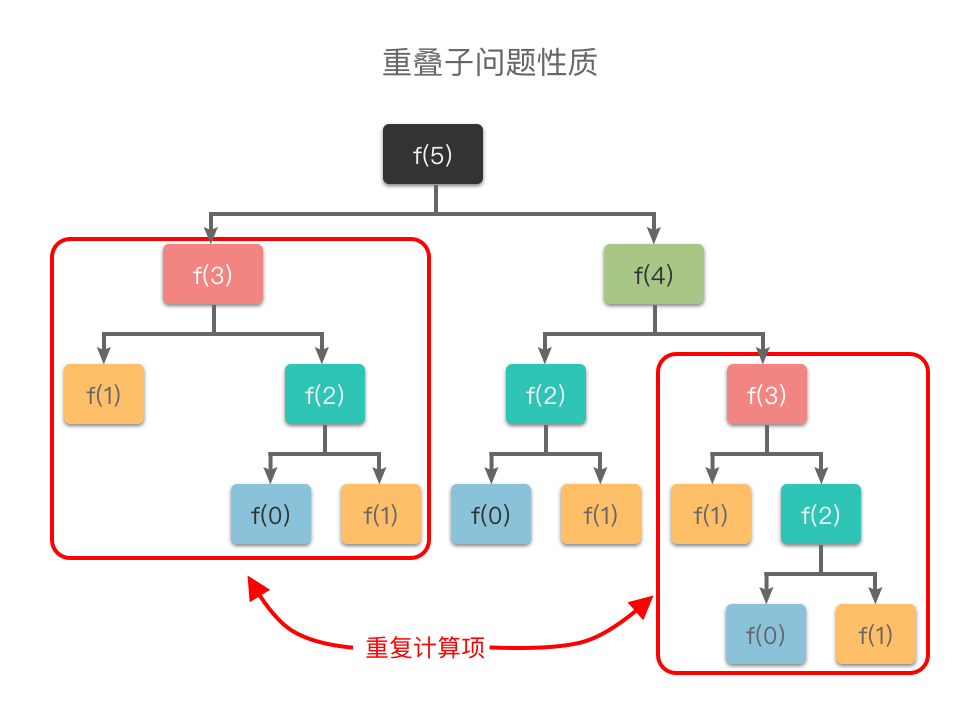
重叠子问题性质：指的是在求解子问题的过程中，有大量的子问题是重复的，一个子问题在下一阶段的决策中可能会被多次用到。如果有大量重复的子问题，那么只需要对其求解一次，然后用表格将结果存储下来，以后使用时可以直接查询，不需要再次求解。

img

之前我们提到的「斐波那契数列」例子中，\(f(0)\)、\(f(1)\)、\(f(2)\)、\(f(3)\) 都进行了多次重复计算。动态规划算法利用了子问题重叠的性质，在第一次计算 \(f(0)\)、\(f(1)\)、\(f(2)\)、\(f(3)\) 时就将其结果存入表格，当再次使用时可以直接查询，无需再次求解，从而提升效率。

7.2.3 无后效性

无后效性：指的是子问题的解（状态值）只与之前阶段有关，而与后面阶段无关。当前阶段的若干状态值一旦确定，就不再改变，不会再受到后续阶段决策的影响。

也就是说，一旦某一个子问题的求解结果确定以后，就不会再被修改。

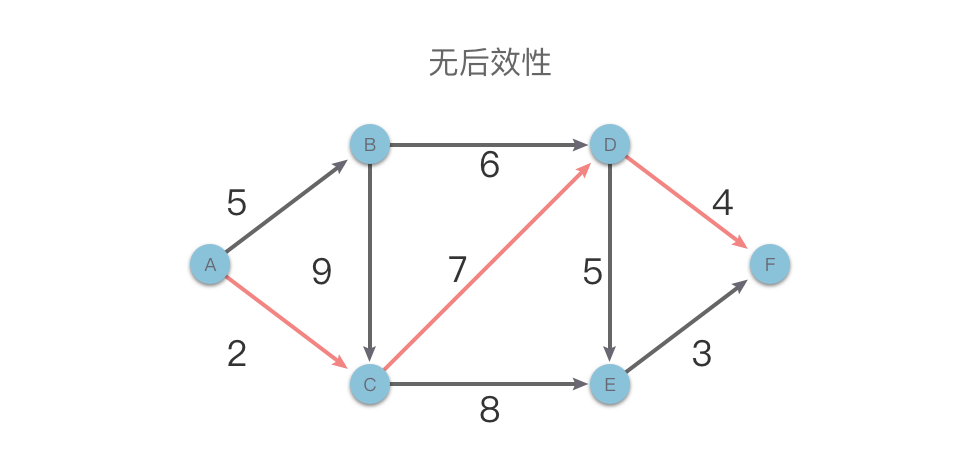
举个例子，下图是一个有向无环带权图，我们在求解从 \(A\) 点到 \(F\) 点的最短路径问题时，假设当前已知从 \(A\) 点到 \(D\) 点的最短路径（\(2 + 7 = 11\)）。那么无论之后的路径如何选择，都不会影响之前从 \(A\) 点到 \(D\) 点的最短路径长度。这就是「无后效性」。

而如果一个问题具有「后效性」，则可能需要先将其转化或者逆向求解来消除后效性，然后才可以使用动态规划算法。

img

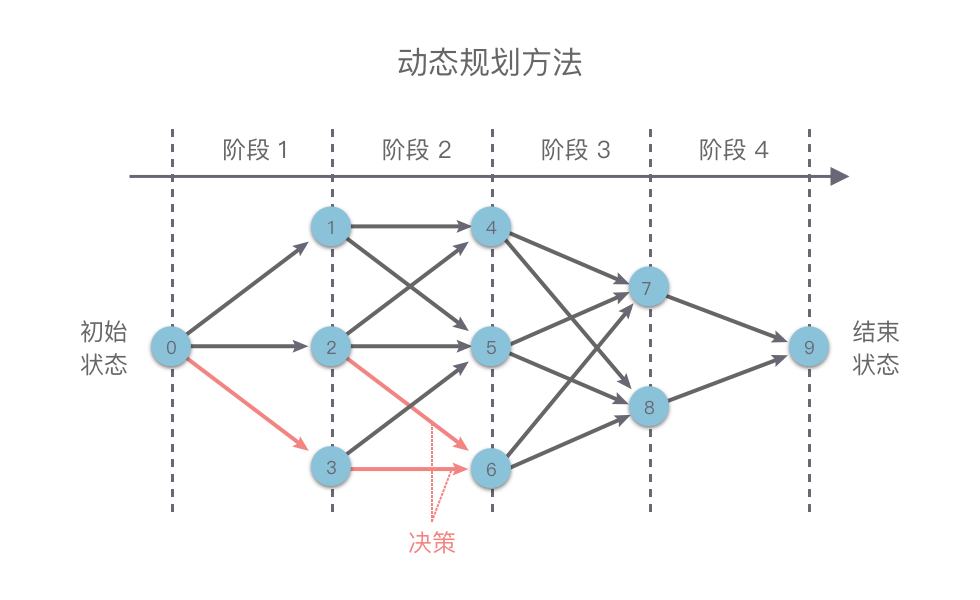
7.3. 动态规划的基本思路

如下图所示，我们在使用动态规划方法解决某些最优化问题时，可以将解决问题的过程按照一定顺序（时间顺序、空间顺序或其他顺序）分解为若干个相互联系的「阶段」。然后按照顺序对每一个阶段做出「决策」，这个决策既决定了本阶段的效益，也决定了下一阶段的初始状态。依次做完每个阶段的决策之后，就得到了一个整个问题的决策序列。

这样就将一个原问题分解为了一系列的子问题，再通过逐步求解从而获得最终结果。

img

这种前后关联、具有链状结构的多阶段进行决策的问题也叫做「多阶段决策问题」。

通常我们使用动态规划方法来解决问题的基本思路如下：

  1. 划分阶段：将原问题按顺序（时间顺序、空间顺序或其他顺序）分解为若干个相互联系的「阶段」。划分后的阶段⼀定是有序或可排序的，否则问题⽆法求解。
    • 这里的「阶段」指的是⼦问题的求解过程。每个⼦问题的求解过程都构成⼀个「阶段」，在完成前⼀阶段的求解后才会进⾏后⼀阶段的求解。
  2. 定义状态：将和子问题相关的某些变量（位置、数量、体积、空间等等）作为一个「状态」表示出来。状态的选择要满⾜⽆后效性。
    • 一个「状态」对应一个或多个子问题，所谓某个「状态」下的值，指的就是这个「状态」所对应的子问题的解。
  3. 状态转移：根据「上一阶段的状态」和「该状态下所能做出的决策」，推导出「下一阶段的状态」。或者说根据相邻两个阶段各个状态之间的关系，确定决策，然后推导出状态间的相互转移方式（即「状态转移方程」）。
  4. 初始条件和边界条件：根据问题描述、状态定义和状态转移方程，确定初始条件和边界条件。
  5. 最终结果：确定问题的求解目标，然后按照一定顺序求解每一个阶段的问题。最后根据状态转移方程的递推结果，确定最终结果。

7.4. 动态规划的应用

7.4.1 Ordering Matrix Multiplication

image-20240415110120170

image-20240415111309249

令\(b_n\)表示计算\(M_1 \cdot M_2 \cdots M_n\)不同方法的数量

我们能够将\(M_1 \cdot M_2 \cdots M_n\)分成两部分，记\(M_{ij} = M_i \cdots M_j\)

那么只需要在矩阵序列中切一刀，就得到两个矩阵序列

此时得到\(b_n\)的递推关系

\[ b_n = \sum_{i=1}^{n-1} b_i b_{n-i}, b_1 =1, b_2 = 1, b_3 = 2 \]

接下来正式计算\(M_1 \cdot M_2 \cdots M_n\)，\(M_i\)是一个\(r_{i-1}\times r_i\) 的矩阵. 用\(m_{ij}\)表示计算\(M_{ij}\)的结果

最后转化为 Mil, Mlj, 以及两个矩阵的相乘

image-20240415112409528

// 利用动态规划，先计算 m11,m22,....mNN
// 再向上计算 m12,m23,...,逐层向上
int Optmatrix(vector<int> &p, vector<vector<int>> &m, int n)
{
    int i, j, k;
    for(i = 1; i <= n; i++) m[i][i] = 0;
    // 接下来依次计算m[i][j]的最小值
    for(i = 1; i <= n -1; i++)
    {
        // 计算m[i][j]的最小值
        for(j = 1; j <= n - i; j++)
        {
            int min = MAX;
            for(k = j; k <= j + i - 1; k++)
            {
                m[j][j+i] = m[j][k] + m[k+1][j+i] + p[j-1]*p[k]*p[j+i];
                if(m[j][j+i] < min) min = m[j][j+i];
            }
            m[j][j+i] = min;
        }
    }
    return m[1][n];
}

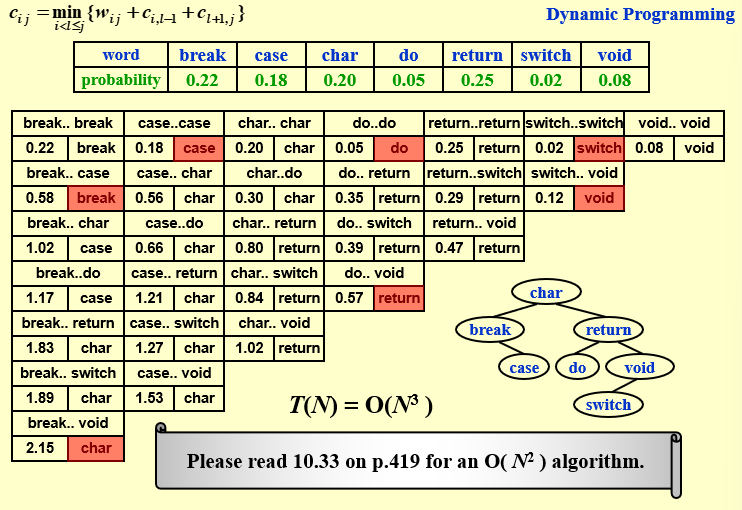
7.4.2 Optimal Binary Search Tree

image-20240415113300514

\(T(N) = \sum_{i =1}^N p_i(1+d_i)\)

image-20240415115018118

依然是拆分成两部分

\(C_{ij} = p_k + cost(L) + cost(R) + weight(L) + weight(R)\)

\(C_{ij} = p_k + C_{i,k-1}+C_{k+1,j} + W_{i.k-1} + W_{k+1,j} = C_{i,k-1} + C_{k+1,j} + W_{ij}\)

此处添加weight(L)和weight(R)的原因是，L和R成为子树之后，所有的深度都会加1，利用pi(1+di)，可知子树所有结点的权重需要累加

image-20240415115815859

从底到顶，先计算长度为1的最小值，在利用长度为1的最小值，计算长度为2的最小值

第一行长度为1，就是本身的weight

第二行长度为2，\(min = (w_ij + min(w_i,w_j))\)

第三行长度为3，以break…char为例

  • break为根结点，break-(case..char) = 0.6 + 0.56 = 1.16
  • case为根结点， break - case -char = 0.6 + 0.22 + 0.20 = 1.02
  • char为根结点， （break..case) char = 0.6 + 0.58 = 1.18

第四行长度为4，以break…do为例

  • break为根结点，break-(case … do) = 0.65 + 0.66 = 1.31
  • case 为根结点， break-case-(char..do) = 0.65 + 0.22 + 0.30 = 1.17
  • char 为根结点， (break..case) - char -do = 0.65 + 0.58 + 0.05 = 1.28
  • do为根结点，(break…char) - do = 0.65 + 1.02 = 1.67
// Dynamic programming function to find the minimum cost  
double DP(vector<double> &weight, vector<vector<double>> &cost, int n)  
{  
    int i, j, k;  
    // Initializing the diagonal of the cost matrix  
    for(i = 1; i <= n; i++) cost[i][i] = weight[i];  

    // Filling up the cost matrix using dynamic programming  
    for(int len = 1; len <= n-1; len++)  
    {  
        for(i = 1; i <= n-len; i++)  
        {  
            j = i + len;  
            double mincost = 1e9;  // Initializing mincost to a very large value  

            // Checking for the base case when len = 1  
            if(len == 1)  
            {  
                cost[i][j] = SumWeight(weight, i, j) + min(weight[i], weight[j]);  
            }  
            else  
            {  
                // Iterating through possible partitions and finding the minimum cost  
                for(k = i; k < j; k++)  
                {  
                    double temp = cost[i][k-1] + cost[k+1][j] + SumWeight(weight, i, j);  
                    if(temp < mincost) mincost = temp;  
                }  
                cost[i][j] = mincost;  // Assigning the minimum cost for this range  
            }  
        }  
    }  
    return cost[1][n];  // Returning the minimum cost for the entire range  
}

7.4.3 All-Pairs Shortest Path

image-20240415121357819

  1. 迪杰斯特拉算法（执行n次）

  2. 动态规划（也就是弗洛伊德算法）。start from \(D^{-1}\),依次计算生成\(D^0,D^1,....D^n\)

能够存在负边，但是不能存在负环

/* A[ ] contains the adjacency matrix with A[ i ][ i ] = 0 */
/* D[ ] contains the values of the shortest path */
/* N is the number of vertices */
/* A negative cycle exists iff D[ i ][ i ] < 0 */
void AllPairs(TwoDimArray A, TwoDimArray D, int N)
{
    int i, j, k;
    for (i = 0; i < N; i++) /* Initialize D */
        for (j = 0; j < N; j++)
            D[i][j] = A[i][j];
    for (k = 0; k < N; k++) /* add one vertex k into the path */
        for (i = 0; i < N; i++)
            for (j = 0; j < N; j++)
                if (D[i][k] + D[k][j] < D[i][j])
                    /* Update shortest path */
                    D[i][j] = D[i][k] + D[k][j];
}

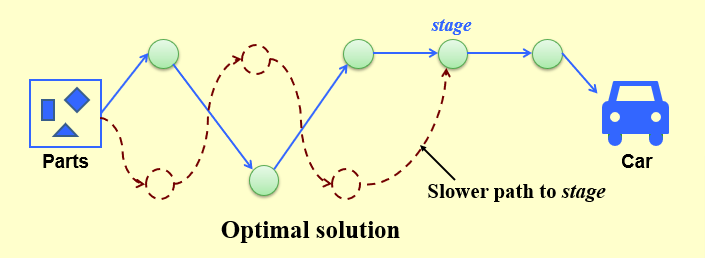
7.4.4 Product Assembly

  1. 暴力法求解

    image-20240415122419701

  2. 动态规划

    image-20240415122445326

    An optimal path to stage is based on an optimal path to stage–1

    当前的最优解，依赖于前一步的最优解

    同一条产品线继续或者从另外一条线进行转移

    O( N ) time + O( N ) space

    f[0][0]=0; L[0][0]=0;
f[1][0]=0; L[1][0]=0;
for(stage=1; stage<=n; stage++){
    for(line=0; line<=1; line++){
    f_stay = f[  line][stage-1] + t_process[  line][stage-1];
    f_move = f[1-line][stage-1] + t_transit[1-line][stage-1];
    if (f_stay<f_move){
        f[line][stage] = f_stay;
        L[line][stage] = line;
    }
    else {
        f[line][stage] = f_move;
        L[line][stage] = 1-line;
    }
    }
}

7.5 习题集

  1. Rod-cutting Problem: Given a rod of total length \(N\) inches and a table of selling prices \(P_L\) for lengths \(L = 1, 2, \cdots , M\). You are asked to find the maximum revenue \(R_N\) obtainable by cutting up the rod and selling the pieces. For example, based on the following table of prices, if we are to sell an 8-inch rod, the optimal solution is to cut it into two pieces of lengths 2 and 6, which produces revenue \(R_8 = P_2 +P_6 = 5+17 = 22\). And if we are to sell a 3-inch rod, the best way is not to cut it at all.

    image-20240417200726635

    Which one of the following statements is FALSE?

    • A. This problem can be solved by dynamic programming

    • B. The time complexity of this algorithm is \(O(N^2)\)

    • C. If \(N\le M\), we have \(R_N = \max \lbrace P_N , \max_{1\le i < N} \lbrace R_i + R_{N-i} \rbrace \rbrace\)

    • D. If \(N>M\), we have \(R_N = \max_{1\le i < N} \lbrace R_i + R_{N-M} \rbrace\)

    B：

    \[ \begin{aligned} &R1 = P1\\ &R2 = max\{P2, R1 + P1\}\\ &R3 = max\{P3, P2 + R1, P1 + R2\}\\ &....\\ &计算R_n需要 1 + 2 + 3 + 4 + ... + n 步 \end{aligned} \]

    D:\(R_N = max_{1<= i < N}\{R_i + R_{N - i} \}\)

  2. In dynamic programming, we derive a recurrence relation for the solution to one subproblem in terms of solutions to other subproblems. To turn this relation into a bottom up dynamic programming algorithm, we need an order to fill in the solution cells in a table, such that all needed subproblems are solved before solving a subproblem. Among the following relations, which one is impossible to be computed?

    • A. \(A(i, j) = min (A(i-1,j), A(i,j-1), A(i-1,j-1))\)

    • B. \(A(i, j) = F(A(min\{i, j\} - 1, min\{i, j\} - 1), A(max\{i, j\} - 1, max\{i, j\} -1))\)

    • C. \(A(i, j) = F(A(i, j -1), A(i - 1, j - 1), A(i - 1, j + 1))\)

    • D. \(A(i,j) = F(A(i-2, j-2), A(i+2,j+2))\)

    要实现动态规划，讲究一个先来后到，显然D的计算顺序有误

    对于C，可以 for i in 0 to n: for j in 0 to n 先计算（i - 1， ）所有的组合，这样 （i - 1， j + 1）的组合也就提前计算了

  3. Given a recurrence equation \(f_{i,j,k} =f_{i,j+1,k}+\min_{0 \le l \le k}\{f_{i-1,j,l}+w_{j,l}\}\). To solve this equation in an iterative way, we cannot fill up a table as follows:

    • A. for k in 0 to n: for i in 0 to n: for j in n to 0

    • B. for i in 0 to n: for j in 0 to n: for k in 0 to n

    • C. for i in 0 to n: for j in n to 0: for k in n to 0

    • D. for i in 0 to n: for j in n to 0: for k in 0 to n

    j 不能增序算，因为 \(f_{i,j,k}\) 依赖于 \(f_{i,j+1,k}\)。

  4. If a problem can be solved by dynamic programming, it must be solved in polynomial time. F

    0-1背包问题可以用DP解，但是复杂度不是多项式的, 原因是输入的数据不是多项式的

背包问题

  1. 背包问题的背景：

    给定背包的承重W, 一堆物品的重量weight[]和价值value[],求背包能装入物品的最大总value

  2. 背包问题的解法：

    定义一个二维数组dp

    其中 $dp[i] [j] $表示：从前 i 件物品中找出一些放入背包，在总重不超过承重W的情况下，能达到的最大value。

    第 i 件物品重量为 weight[i]，价值为 value[i]，根据第 i 件物品是否添加到背包中，可以分两种情况讨论：

    • 第 i 件物品的重量超过背包承重，即 weight[i] > j。此时就算拿出背包中的所有物品也无法放下，所以它不可能被放入背包，因此有：dp[i][j] = dp[i-1][j]
    • 第 i 件物品可以添加到背包中（可能拿出一些已有物品）。此时也可以有放入与不放入两种情况，应取value更大的那种。
      • 若不放入，有：dp[i][j] = dp[i-1][j]
      • 若放入，情况变为从某个状态下加入第i件物品并达到dp[i][j]结果，可知前一状态时的背包承重应为 j-weight[i]。因此有：dp[i][j] = dp[i-1][ j-weight[i] ] + value[i]。

  3. 得到递推式：

dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])

```cpp
int dp[W];
memset(dp, 0, sizeof(dp));
for(int i = 0; i < n; i++)
{
    for(int j =  W; j >= 1; j--)
    {
        if(j >= weight[i])
        {
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
}
return dp[W];
```

For problem i, Bob will need time[i] to solve it and obtains the corresponding score[i], or he may choose not to solve it at all. Bob will be happy when he obtains a total score no less than happy_score. You are supposed to find the minimum time needed for Bob to be happy. The function need_time must return the minimum time, or -1 if it is impossible for Bob to obtain a score no less than happy_score.

Format of function:

int need_time(const int time[], const int score[], int happy_score, int n);

Here n (1≤n≤ MAXN) is the number of problems;

happy_score (1≤ happy_score ≤ MAXS) is the minimum score for Bob to be happy;

time[] is the array to store time[i] (1≤time[i]≤100) which is the time to solve problem i;

score[] is the array to store score[i] (1≤score[i]≤100) which is the score Bob gets for solving problem i.

PTA的题目要求是：

1.开心值总和 >= happy_score 2.所花时间总和最少

上述的背包问题不再适用恰好是其反面

从逆向思维出发：要求score总和小于 sum_score - happy_score,并且总time最大，符合背包的假设.最后只需要用sum_time-逆向时间的最大值即可得到正向的最小时间

int need_time(const int time[], const int score[], int happy_score, int n)
{
    // 背包问题
    int sum_score = 0;
    int sum_time = 0;
    for (int i = 0; i < n; i++)
    {
        sum_score += score[i];
        sum_time += time[i];
    }
    if(sum_score < happy_score) return -1;

    // 我们要计算，不达到happy_score的情况下，最多需要多少时间
    // 这样就可以用总时间减去这个时间，就是最少时间
    int dp[sum_score];
    memset(dp, 0, sizeof(dp));
    for(int i = 0; i < n; i++)
    {
        for(int j = sum_score - happy_score; j >= score[i]; j--)
        {
            dp[j] = dp[j] > dp[j - score[i]] + time[i] ? dp[j] : dp[j - score[i]] + time[i];
        }
    }
    return sum_time - dp[sum_score - happy_score];
}