9. Greedy Algorithms¶

约 5093 个字 13 行代码预计阅读时间 26 分钟

9.1 Introduction¶

Optimization Problems：

Given a set of constraints and an optimization function. Solutions that satisfy the constrains are called feasible solutions. A feasible solution for which the optimization function has the best possible value is called an optimal solution.

给定一组约束和一个优化函数。满足约束条件的解称为可行解。优化函数具有最佳可能值的可行解称为最优解。

Greedy Method：

Make the best decision at each stage, under some greedy criterion. A decision made in one stage is not changed in a later stage, so each decision should assure feasibility.

在某个贪心准则下，在每个阶段做出最佳决定。在一个阶段做出的决定在以后的阶段不会改变，因此每个决定都应确保可行性。

注意： 贪婪算法仅在局部最优值等于全局最优值时才有效。贪婪算法并不能保证最优解。但是，它通常生成的解在值（启发式）上非常接近最优。

9.1.1 Elements of the Greedy Stratege¶

Cast the optimization problem as one in which we make a choice and are left with one subproblem to solve.

将优化问题转换为:我们做出贪心选择后，剩余一个子问题需要解决。
Prove that there is always an optimal solution to the original problem that makes the greedy choice, so that the greedy choice is always safe.

证明做出贪心选择后，原问题总是存在最优解，即贪心选择总是安全的
Demonstrate optimal substructure by showing that, having made the greedy choice, what remains is a subproblem with the property that if we combine an optimal solution to the subproblem with the greedy choice we have made, we arrive at an optimal solution to the original problem.

证明做出贪心选择后，剩余的子问题满足性质：其最优解与贪心选择组合即可得到原问题的最优解，这样就得到了最优子结构。

能用贪心算法解决先用贪心解决，不能再用dp

9.1.2 贪心选择性质和最优子结构¶

对于大部分问题贪心算法的证明而言，贪心选择性质和最优子结构是两个关键要素

贪心选择性质：(贪心选择的结果一定是最优解的一部分)我们可以通过做出局部最优（贪心）选择来构造全局最优解。换句话说，当进行选择时，我们直接做出在当前问题中看来最优的选择，而不必考虑子问题的解。
- 这也是贪心算法与动态规划的不同之处。在动态规划方法中，每个步骤都要进行一次选择，但选择通常依赖于子问题的解。
- 但在贪心算法中，我们总是做出当时看来最佳的选择，然后求解剩下的唯一的子问题。贪心算法进行选择时可能依赖之前做出的选择，但不依赖任何将来的选择或是子问题的解。
通过对输入进行预处理或者使用适合的数据结构（通常是优先队列），我们通常可以使贪心选择更快速。在活动选择问题中，假定我们已经将活动按结束时间单调递增顺序排好序，则对每个活动只需处理一次。
最优子结构：（用贪心策略选择$a_1$之后得到子问题$S_1$,那么$a_1$和子问题$S_1$的最优解合并一定能够得到原问题的一个最优解）一个问题的最优解包含其子问题的最优解。

如前活动选择问题所述，通过对原问题应用一次贪心选择即可得到子问题，那么最优子结构的工作就是论证：将子问题的最优解与贪心选择组合在一起的确能生成原问题的最优解。这种方法隐含地对子问题使用了数学归纳法，证明了在每个步骤对子问题进行贪心选择，一步一步推进就会生成原问题的最优解。

9.2 Activity Selection Problem¶

definition "Activity Selection Problem"

Given a set of activities$S = { a_1, a_2, ..., a_n }$ that wish to use a resouce (e.g. a classroom).

Activities$a_i$ and$a_j$ are compatible if$s_i \geq f_j$ or$s_j \geq f_i$ (i.e. their time intervals do not overlap).

给定一个活动集合$S = {a1, a2, . . . , an}$，其中每个活动$ai$都有一个开始时间$si$和结束时间$fi$，且$0 ≤ s_i < f_i < ∞$。(Each$a_i$ takes place during a time interval$[s_i, f_i)$.)如果活动$a_i$ 和$a_j$满足$f_i ⩽ s_j$或者$f_j ⩽ s_i$，则称活动$a_i$和$a_j$ 是兼容的（即二者时间不会重合）。活动选择问题就是要找到一个最大的兼容活动子集。

Goal: Select a maximum-size subset of mutually compatible activities.

Assume$f_1\geq f_2 \geq ... \geq f_n$.

抽象来说就是一个一维的密铺问题。给定时间线上的若干区间$[s_i, f_i)$，求出最多能不重叠地在这个时间线上放置多少个区间。题目额外保证了输入数据是根据$f_i$ 有序的

9.2.1 动态规划¶

动态规划：

设$S_{ij}$表示活动$a_i,a_j$之间的最大兼容活动集合（开始时间在$a_i$结束之后，结束时间在$a_{j}$开始之前），其大小记为$c_{ij}$

$$ c_{ij} = max{c_{ik} + c_{kj} + 1 | f_i<= s_k < f_k <= s_j} $$

此处的加1是因为，需要额外添加a_k,c_{ik}表示的是a_k开始之前，c_{kj}表示的是a_k开始之后，空余出一个a_k

时间复杂度为：
- 先计算间隔k=1，$c_{i,i+1} = 0$ ——$N - 1$
- 再计算间隔k=2，$c_{i,i+2}$ ——$（k - 1)*(N - k)$
$$ \begin{aligned} &\sum_{k=2}^{N-1} (k-1)\times (N-k) = (N-2)+2 \times (N-3)+...+ (N-2) \times 1= N \times \sum_{k=2}^{N-1} (k-1) - \sum_{k=2}^{N-1} k\times (k-1) \ \end{aligned} $$

其时间复杂度为$O(N^2)$。
背包问题思路：

设$Si$表示活动$a1, a2, . . . , ai$的最大兼容活动集合，其大小记为$ci$(活动$a_i$结束之前)，那么我们有

$$ c_i = max{c_{i-1}, c_{k(i)}+1} $$

分为两个情况讨论：
- 活动$a_i$不放，$c_i = c_{i-1}$
- 活动$a_i$放置，但是得取出一些活动.其中$k(i)$ 表示在$1 ⩽ k ⩽ i$中，$f_k ⩽ s_i$ 且$c_k$最大的$k$，即不与ai 冲突的最晚结束的活动。于是$c_i = c_{k(i)} +1$
其时间复杂度为$O(N^2)$。
对于带权重问题，贪心算法无法求得最优解,但是动态规划的方法依然成立

9.2.2 贪心算法¶

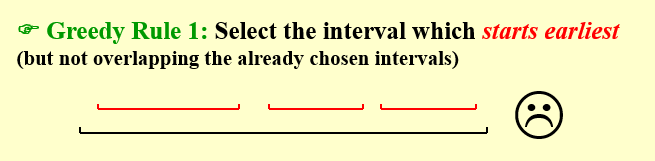
贪心算法：一个可能正确的贪心策略为从前到后每次选择不冲突的最早结束的活动

贪心算法一：哪门课先开始我先选哪门课，但是显然不对。

反例：开始最早结束最晚
贪心算法二：每次都选区间长度最少的，虽然看起来能让它“相对比较多”，但是显然也无法保证结果的最优性
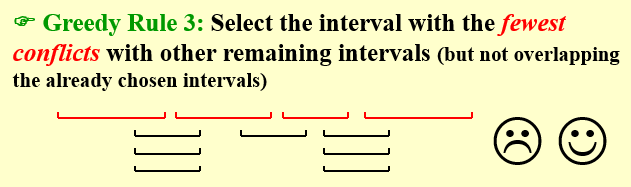
贪心算法三：选择重叠最少的
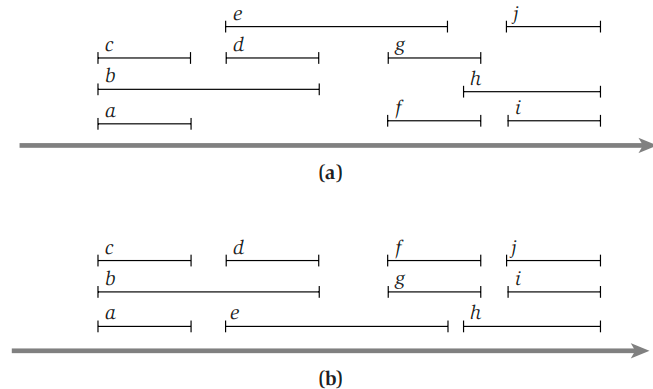
贪心算法四：选择最早结束的

首先我们先来验证这一策略的正确性

令$S_k = \{a_i \in S | s_i >= f_k\}$,$S_k$表示在$a_k$结束后开始的任务。当我们做出贪心选择，选择$a_1$后，剩下的我们只需要求解S1这一子问题。

如果$a_1$确实在最优解中，那么原问题的最优解显然是由活动$a_1$和子问题$S_1$的最优解构成。（这一点称之为贪心算法的最优子结构）。之后子问题$S_1$我们又可以按照贪心策略选择新的结束时间最早的活动，以此类推，能够得到全部的解。

接下来的问题转化为：贪心选择最早结束的活动是否是最优解的一部分？

【定理：活动选择问题的贪心选择性质】考虑任何非空子问题$S_k$，并设$a_m$ 是$S_k$ 中结束时间最早的活动。然后$a_m$包含在$S_k$的相互兼容活动的一些最大大小的子集中。
- 令$A_k$是$S_k$的一个最大兼容活动子集，且$a_{ef}$是$A_k$中结束时间最早的活动。
- 如果$a_m = a_{ef}$,上述定理直接成立，此时$S_k$中结束时间最早的活动$a_m$已经包含在最大兼容活动子集$A_k$中
- 如果$a_m != a_{ef}$,则用$a_m$替代$a_{ef}$,因为$a_m$是$S_k$中结束时间最早的活动，说明$a_m$的结束时间比$a_{ef}$的结束时间还早，也就是得到的新的最优解$A_{k'}$,也是$S_k$的一个最大兼容活动子集。
上述的思想是：“交换参数法”，假设存在一个最优选择，其中某个元素可能不在我们的贪心选择中，然后我们可以通过交换贪心选择和最优选择的元素来构造一个不可能变差的解，这样我们就能说明贪心选择得到的结果也是最优选择的一种

【定理：活动选择问题的最优子结构】在活动选择问题中，用贪心策略选择$a_1$之后得到子问题$S_1$,那么$a_1$和子问题$S_1$的最优解合并一定能够得到原问题的一个最优解

反证法：假设$a_1$和子问题$S_1$的最优解$C_1$合并得到的解$\(C$\)不是原问题的一个最优解
- 先假设$C'$是原问题的一个最优解，那么$|C'| > |C|$。
- 根据贪心选择的性质，$a_1$的结束时间肯定比$C'$中第一个元素的结束时间早，所以我们用$a_1$替换掉$C'$中的第一个元素，不会使结果变差，$|C''| = |C'| > |C|$
- 接下来我们去除$C''$中的$a_1$,得到子问题$S_1$的一个解$C_1''$,由于$|C''| > |C|$,所以$|C_1''| > |C_1|$,这与$C_1$是子问题$S_1$的最优解矛盾
时间复杂度为：如果结束时间已经完成排序，我们只需要按照结束时间升序遍历一遍所有活动，就能在$O(N)$的时间内找到最优解。没有排序，就先以$O(NlogN)$的时间完成排序，最后的总时间复杂度就是$O(NlogN)$

综上：

我们首先根据贪心选择性质找到最早结束的活动$a_1$，根据最优子结构性质可知，它和$S_1$的最优解一起可以形成全问题的最优解，然后我们的任务就变成了找$S_1$ 的最优解。重复贪心选择性质，我们要找到$S_1$ 中最早结束的$a_{i1}$ 作为贪心选择，这样根据最优子结构，$S_1$ 的最优解又可以表达为$a_{i1}$和剩余子问题$S_{i1}$ 的最优解的组合，然后我们找$S_{i1}$ 的最优解，用贪心选择然后得到剩余子问题...... 以此类推，利用归纳法即可得到，直到子问题为空时我们可以得到整个问题的最优解。

【变体1：加权活动选择问题】每一个活动都有一个权重$w_i$,我们希望找到一个最大权重的兼容活动集合。此时上述的贪心算法失效，不再是希望包含的活动越多越好。

可以使用动态规划带权重的方法进行解决。

【变体2：区间调度问题】问题不再是最大化兼容集合的大小或者权重，而是转化为：每一个活动都需要教师进行举办，考虑将所有的活动分配到最少的教室，且每个教室的活动不冲突。

思路是：将所有活动按照开始时间进行排序，设置教室的初始数量为1，从前往后遍历，每次选择一个活动，先看当前教室有无空余，如果全部都冲突就新开一个教室。

简化后：问题转化为，在某一时段活动冲突的最大数量。假设最多出现3个活动同时进行，最多分配3个教室。因为只有在全部冲突时才能新开一个教室，所以分配第四个教室意味着前三个教室都有活动，有四个活动同时进行，与前提矛盾

9.3 调度问题¶

假设我们现在有$n$ 个任务，每个任务$i$都有一个正的完成需要的时间$l_i$和一个权重$w_i$。假定我们只能按一定顺序依次执行这些任务，不能并行。

记$\sigma$为一种调度方法，在调度$\sigma$中，任务$i$的完成时间为$C_i(\sigma)$,表示任务$i$之前的任务完成时间之和加上任务$i$本身的完成时间要求：最小化加权完成时间之和 $$ T = min \sum_{i = 1} ^ n w_i C_i(\sigma) $$ 举个例子，有三个任务，$l_1 = 1，l_2 = 2，l_3 = 3，w_1 = 3，w_2 = 2，w_3 = 1$。如果我们把第一个任务放在最前，第二个放在其次，第三个放在最后，那么三个任务的完成时间就是1、3、6，因此加权时间和为$3 × 1 + 2 × 3 + 1 × 6 = 15$。如果读者检查全部的六种排序，这的确是最小的那一个。

假如所有的任务所需的时间都相等，为了使加权完成时间最小，显然要将权重最大时间最短的任务放在前面。

于是我们得到以下的贪心策略：

计算每个任务i的$w_i - l_i$,按照大小降序调度任务

计算每个任务i的$\dfrac{w_i}{l_i}$,按照大小降序调度任务

随便举个例子，看看哪个方法能得到正确的结果。有两个任务，$l_1 = 5, l_2 = 2, w_1= 3, w_2 = 1$

按照第一个贪心策略进行计算，先执行任务2，再执行任务1，总时间为$2 + 3 * 7 = 23$

按照第二个贪心策略进行计算，先执行任务1，再执行任务2，总时间为$3 * 5 + 7 = 22$

发现还是贪心策略2更胜一筹

【定理：调度问题的贪心选择性质】令$i$是当前$w_i / l_i$最大的任务，那么一定存在将任务$i$排在首位的最优调度方式

证明：依然是“交换参数法”，假设存在一个最优解C，如果它的第一个任务是$i$，那么定理成立。如果它的第一个任务是$j$，且$i != j$,那么我们就把任务$i$往前移动，直到第一位。

现假设，原先的最优解C中任务$j$是第一位，任务$i$是第二位，最优解$C'$中任务i是第一位，任务j是第二位。

为什么仅仅考虑第一位和第二位交换呢？假如j，i的前面有n个任务，显然前n个任务的加权完成时间是固定的，对于任务i和任务j，无非是需要额外添加一个常数（前n个任务的时间总和）×权重，发现最终相减的时候能够消去

\[ \begin{aligned} & t_1 = w_j \times l_j + w_i \times (l_j + l _i) \\ & t_2 = w_i \times l_i + w_j \times (l_i + l_j) \\ & \Delta t = t_1 - t_2 = w_i \times l_j - w_j \times l_i \\ & \dfrac{w_i}{l_i} >= \dfrac{w_j}{l_j} \rightarrow w_i \times l_j >= w_j \times l_i \rightarrow \Delta t >= 0 \end{aligned} \]

故把$i$往前换，加权时间和一定不会变大，故仍然保证最优解。那么我们就可以不断把$i$往前换，直到它在第一个位置，这样就证明了贪心选择性质。

【定理：调度问题的最优子结构】在调度问题S中，我们用贪心策略首先选择具有最大$w_i / l_i$的任务$i$ , 任务$i$和剩余子问题$S_1$（除任务i外任务中寻找一个最小化加权完成时间之和的解）的最优解$C_1$一起构成原问题的一个最优解$C$。

依然是采用反证法：

如果C不是最优解，一定存在最优解$C'$,它对应的加权完成时间之和$T' < T$

根据贪心选择性质，如果把$C'$中的$i$ 不断通过相邻交换换到第一个位置，情况一定不会变差，因此还是最优解，我们将这一新的最优解记为$C''$。于是$C''$ 在选择了$i$ 之后，剩下的选择实际上也是$S1$ 的一个解，由于$T'' <= T' < T$，这表明$C''$ 中对应的$S1$ 的解必定比$C1$ 更好，但我们知道$C1$是最优解，因此得到矛盾。所以$C1$ 和$i$一起一定构成了原问题的一个最优解C。

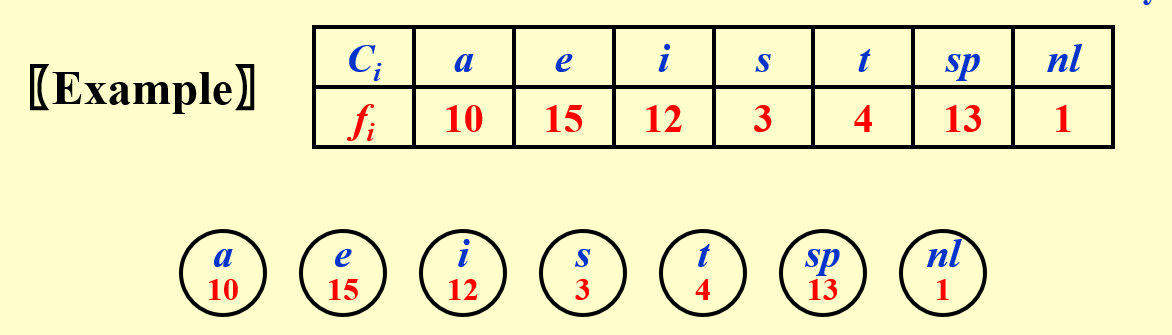
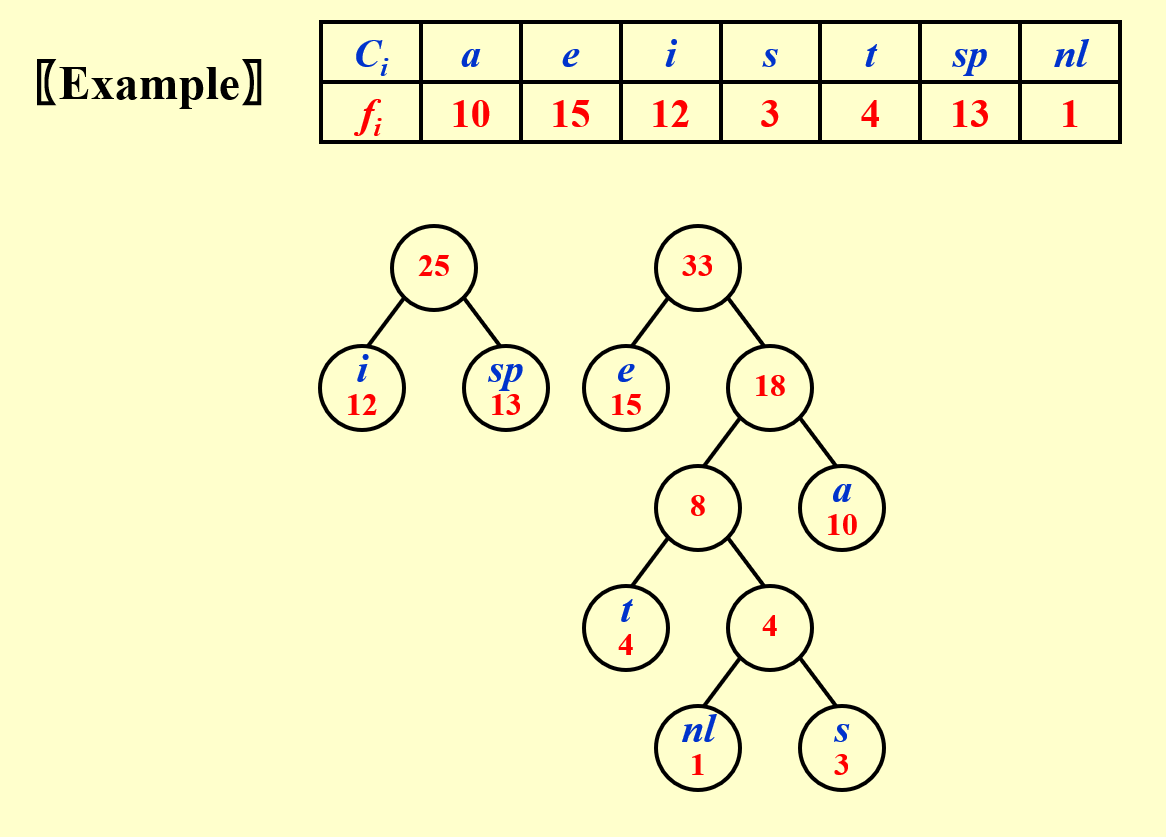
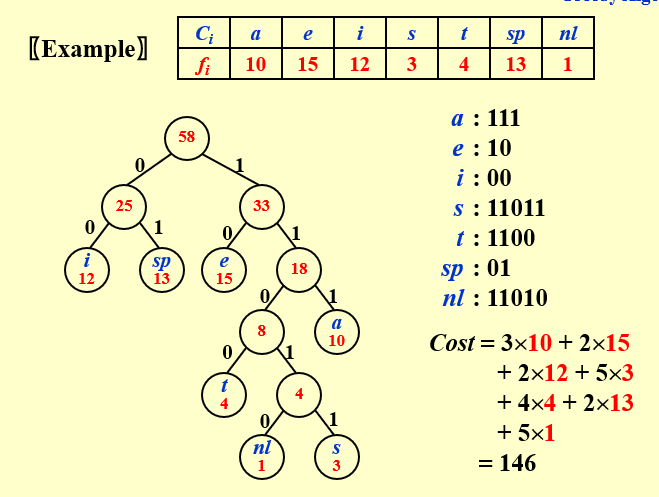
9.4 Huffman Codes¶

Huffman Codes——for file compression

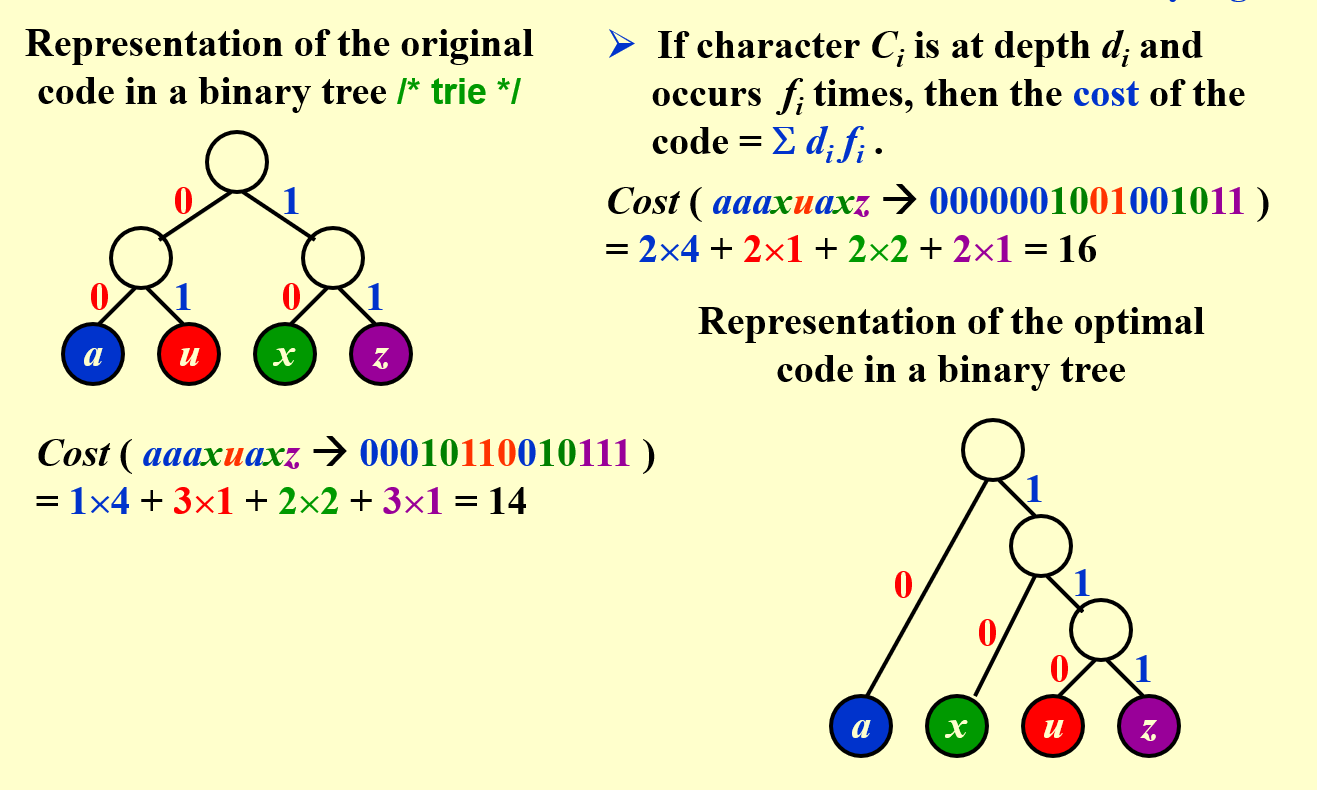
〖Example〗 Suppose our text is a string of length 1000 that comprises the characters a, u, x, and z. Then it will take 8000 bits to store the string as 1000 one-byte characters.

We may encode the symbols as a = 00, u = 01, x = 10, z = 11. For example, aaaxuaxz is encoded as 0000001001001011. Then the space taken by the string with length 1000 will be 2000 bits + space for code table.

/ log C bits are needed in a standard encoding where C is the size of the character set /

现在将频率考虑在内：

In string aaaxuaxz , f(a) = 4, f(u) = 1, f(x) = 2, f(z) = 1.

The size of the coded string can be reduced using variable-length codes, for example, a = 0, u = 110, x = 10, z = 111.$\rightarrow 00010110010111$

防止出现歧义，也就是防止出现一个字符的编码是另一个字符的前缀

void Huffman ( PriorityQueue  heap[ ],  int  C )
{   consider the C characters as C single node binary trees,
     and initialize them into a min heap;
     for ( i = 1; i < C; i++ ) { 
        create a new node;
        /* be greedy here */
        delete root from min heap and attach it to left_child of node;
        delete root from min heap and attach it to right_child of node;
        weight of node = sum of weights of its children;
        /* weight of a tree = sum of the frequencies of its leaves */
        insert node into min heap;
   }
}

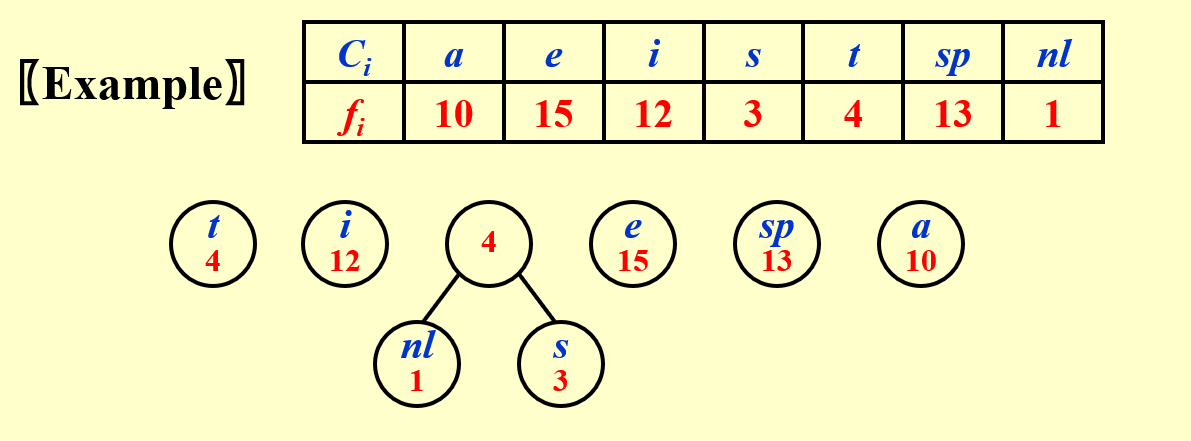
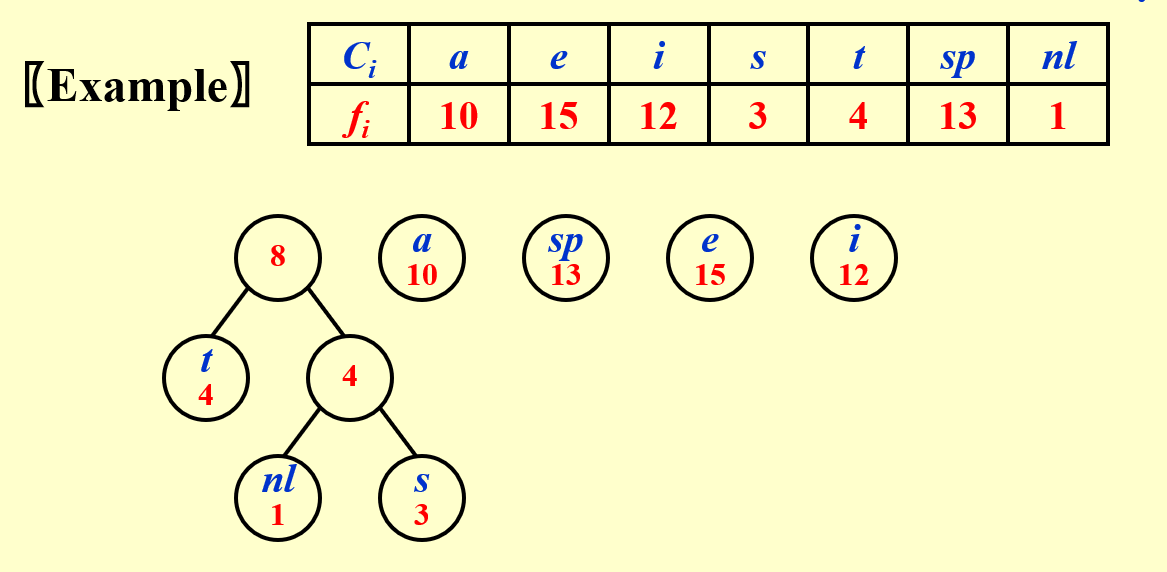
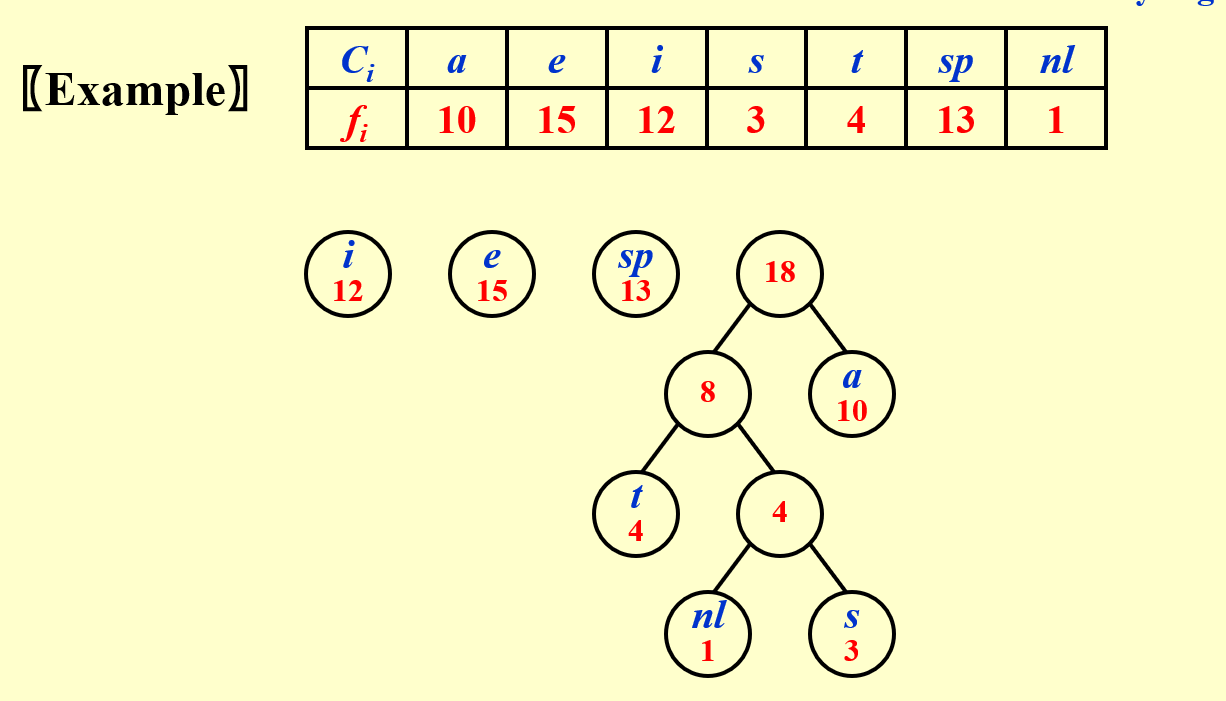
算法思路是：

从根据频率建立的最小堆中取出并删除root，作为新node的左儿子

从最小堆中取出并删除root，作为新node的右儿子

新node的weight就是两个儿子的weight之和

最后将新的node插入到最小堆中

将C个character，不断地合并成一个，需要执行C-1次

时间复杂度为$T = O(ClogC)$

1. 频率最低的两位编码只有最后一位不同

2. 频率最高的放在根结点附近（高位）

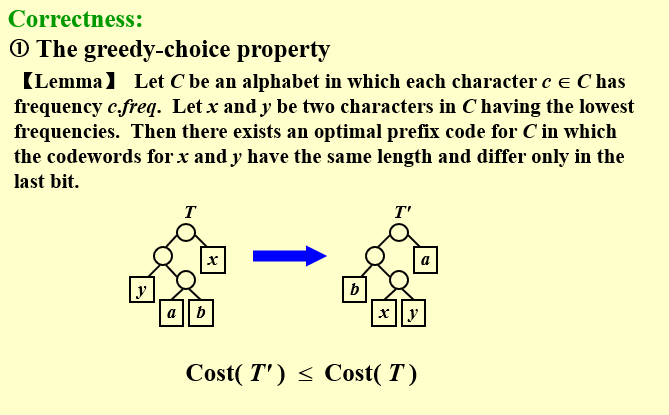
【定理：贪婪选择性质】$C$ 为一个字母表，其中每个字符$c ∈ C$都有一个频率$c.freq$。令$x$和$y$是C 中频率最低的两个字符。那么存在C 的一个最优前缀码，x 和y 的码字长度相同，且只有最后一个二进制位不同。

频率最低的character$x,y$的编码长度相同，且具有相同前缀，这个编码方式一定最优解

我们的思路是：令$T$表示任意一个最优前缀码对应的编码树，对其进行修改，得到另一个最优前缀码的编码树$T'$,使得在新树中，x和y是深度最大的叶结点，且为兄弟节点，这意味着x和y的编码具有相同长度，且只有最后一位不同。

经验证，显然$Cost(T') <= Cost(T)$,新的树的代价小于等于原来的树，得到新的最优解

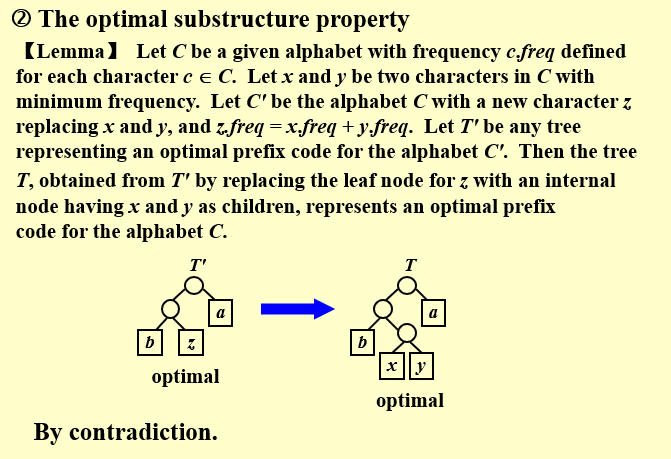
【定理：最优子结构】$C$ 为一个字母表，其中每个字符$c ∈ C$ 都有一个频率$c.freq$。令$x$和$y$表示$C$ 中频率最低的两个字符。令$C'$ 为$C$ 去掉字符$x$和$y$，加入一个新字符$z$后的字母表。我们给$C'$也定义频率集合，不同之处只是$z.freq = x.freq + y.freq$。令$T'$ 为$C'$的任意一个最优前缀树，那么我们可以将$T'$中叶结点$z$ 替换为一个以$x$和$y$ 为孩子的内部结点得到一个$C$的一个最优前缀码树$T$。

如果上面这一命题正确，那么我们每次合并$x$ 和$y$ 得到$z$之后，按照没有$x$ 和$y$，只有$z$的子问题继续推进我们的贪心算法可以得到$T'$ 这一子问题的最优解，它和合并$x$ 和$y$ 得到$z$ 这一前面已经验证正确性的贪心选择一起，就构成了整体的最优解。

反证法：记$Cost(T)$为树T的代价，即所有字母的编码长度之和。

$T'$是由$T$删除$x，y$结点，替换为$z$结点得到的，其中$z.freq = x.freq + y.freq$,这也就意味着，将$x,y$的编码长度减一，树的深度-1，所以$Cost(T') = Cost(T) - x.freq -y.freq$。

现在假设$T$不是C的最优前缀编码树，存在树$T''$使得$Cost(T'') < Cost(T)$,对$T''$同样进行删除$x,y$结点，替换为$z$结点的操作得到新的树$T'''$

\[ \begin{aligned} &Cost(T''') = Cost(T'') - x.freq - y.freq < Cost(T) - x.freq - y.freq\\ &Cost(T') = Cost(T) - x.freq - y.freq\\ &\Rightarrow Cost(T''') < Cost(T') \end{aligned} \]

这与$T'$是$C'$的最优前缀编码树矛盾，所以$T$一定是$C$的最优前缀编码树。

9.5 习题集¶

Greedy algorithm works only if the local optimum is equal to the global optimum.

T，只有在局部解和全局解相等的时候可以用
In a greedy algorithm, a decision made in one stage is not changed in a later stage.

T，做出选择后不会改变
Let$C$ be an alphabet in which each character$c$ in$C$ has frequency$c.freq$. If the size of$C$ is$n$, the length of the optimal prefix code for any character$c$ is not greater than$n-1$.

T，最长情况也就是skew tree，最后一层必有两个结点
哈夫曼编码是一种最优的前缀码。对一个给定的字符集及其字符频率，其哈夫曼编码不一定是唯一的，但是每个字符的哈夫曼码的长度一定是唯一的。

F, 哈夫曼字符的频率相同时每个字符的码长不是确定的。
Consider the problem of making change for$n$ cents using the fewest number of coins. Assume that each coin's value is an integer.The coins of the lowest denomination（面额） is the cent.

(I) Suppose that the available coins are quarters (25 cents), dimes (10 cents), nickels (5 cents), and pennies (1 cent). The greedy algorithm always yields an optimal solution.

(II) Suppose that the available coins are in the denominations that are powers of c, that is, the denominations are$c^0$,$c^1$, ...,$c^k$ for some integers$c>1$ and$k>=1$. The greedy algorithm always yields an optimal solution.

(III) Given any set of$k$ different coin denominations which includes a penny (1 cent) so that there is a solution for every value of$n$, greedy algorithm always yields an optimal solution.

Which of the following is correct?
- A. Statement (I) is false.
- B. Statement (II) is false.
- C. Statement (III) is false.
- D. All of the three statements are correct.
c. Let the coin denominations be$\{1, 3, 4\}$, and the value to make change for be$6$. The greedy solution would result in the collection of coins$\{1, 1, 4\}$ but the optimal solution would be$\{3, 3\}$.**
Consider the problem of making change for$n$ cents using the fewest number of coins. Assume that each coin's value is an integer.

a. Describe a greedy algorithm to make change consisting of quarters, dimes, nickels, and pennies. Prove that your algorithm yields an optimal solution.

b. Suppose that the available coins are in the denominations that are powers of$c$, i.e., the denominations are$c^0, c^1, \ldots, c^k$ for some integers$c > 1$ and$k \ge 1$. Show that the greedy algorithm always yields an optimal solution.

c. Give a set of coin denominations for which the greedy algorithm does not yield an optimal solution. Your set should include a penny so that there is a solution for every value of$n$.

d. Give an$O(nk)$-time algorithm that makes change for any set of$k$ different coin denominations, assuming that one of the coins is a penny.

a. Always give the highest denomination coin that you can without going over. Then, repeat this process until the amount of remaining change drops to$0$.

b. Given an optimal solution$(x_0, x_1, \dots, x_k)$ where$x_i$ indicates the number of coins of denomination$c_i$ . We will first show that we must have$x_i < c$ for every$i < k$. Suppose that we had some$x_i \ge c$, then, we could decrease$x_i$ by$c$ and increase$x_{i + 1}$ by$1$. This collection of coins has the same value and has$c − 1$ fewer coins, so the original solution must of been non-optimal. This configuration of coins is exactly the same as you would get if you kept greedily picking the largest coin possible. This is because to get a total value of$V$, you would pick$x_k = \lfloor V c^{−k} \rfloor$ and for$i < k$,$x_i\lfloor (V\mod c^{i + 1})c^{-i} \rfloor$. This is the only solution that satisfies the property that there aren't more than$c$ of any but the largest denomination because the coin amounts are a base$c$ representation of$V\mod c^k$.

c. Let the coin denominations be$\{1, 3, 4\}$, and the value to make change for be$6$. The greedy solution would result in the collection of coins$\{1, 1, 4\}$ but the optimal solution would be$\{3, 3\}$.

d. See algorithm$\text{MAKE-CHANGE}(S, v)$ which does a dynamic programming solution. Since the first forloop runs$n$ times, and the inner for loop runs$k$ times, and the later while loop runs at most$n$ times, the total running time is$O(nk)$.

9.5.1 Huffman¶

判断题

Given a Huffman tree for N (≥2) characters, all with different weights. The weight of any non-leaf node must be no less than the weight of any node on the next lower level. T，非叶子结点的weight是它的儿子的weight之和

选择题

定不小于下一层任一结点的权值 D 该树一定是一棵完全二叉树
Given a piece of text which consists of characters {a, b, c, d}, with the frequencies of occurrence being {4, 2, 5, 1}, respectively. How many bits are saved by Huffman code comparing to the equal-length code?
```
   12
   /  \   
   5(0) 7
      / \
      3   4(11)
      /\
   1(100)  2(101)
```
计算的是带权路径长度之差：$12 \times 2 - 4 \times 2 - 3 \times 3 - 5 \times 1 = 24 - 22 = 2$
哈夫曼树是n个带权叶子结点构成的所有二叉树中（）最小的二叉树。

A. 权值

B. 高度

C. 带权路径长度(weight * 编码数)

D. 度
关于Huffamn树，如下说法错误的是（）

A. 多于1个叶子结点的Huffman树中不存在度为1的结点

B. Huffman树中，任意调整结点左右孩子的顺序，不影响带权路径长度

C. Huffamn树的带权路径长度最大

D. Huffman树中，权值越大的叶子结点离根结点越近
设给定权值总数有n 个,其哈夫曼树的结点总数为($2n - 1$)
设哈夫曼树中有199个结点，则该哈夫曼树中有（100）个叶子结点。
给定一段文本中的4个字符(a, b, c, d)。设a和b具有最低的出现频率。下列哪组编码是这段文本可能的哈夫曼编码？

A. a: 000, b:001, c:01, d:1

B. a: 000, b:001, c:01, d:11

C. a: 000, b:001, c:10, d:1

D. a: 010, b:001, c:01, d:1
给定一段文本中的 4 个字符 (u,v,w,x) 及其出现频率 (fu ,fv ,fw ,fx )。若对应的哈夫曼编码为 u: 00, v: 010, w: 011, x: 1，则下列哪组频率可能对应 (fu ,fv ,fw ,fx )？

A. 15, 23, 16, 45

B. 30, 21, 12, 33

C. 41, 12, 20, 32

D. 55, 22, 18, 46