Image_Classification¶

约 8023 个字 63 行代码预计阅读时间 41 分钟

概念¶

目标：这一节我们将介绍图像分类问题。所谓图像分类问题，就是已有固定的分类标签集合，然后对于输入的图像，从分类标签集合中找出一个分类标签，最后把分类标签分配给该输入图像，或者简单的说，就是对于一个给定的图像，预测它属于哪个类别（或者给出属于一系列不同标签的可能性）。 虽然看起来挺简单的，但这可是计算机视觉领域的核心问题之一，并且有着各种各样的实际应用。在这里我们面临的挑战就是 语义鸿沟(semantic gap)。在后面的课程中，我们可以看到计算机视觉领域中很多看似不同的问题（比如物体检测和分割），都可以被归结为图像分类问题。

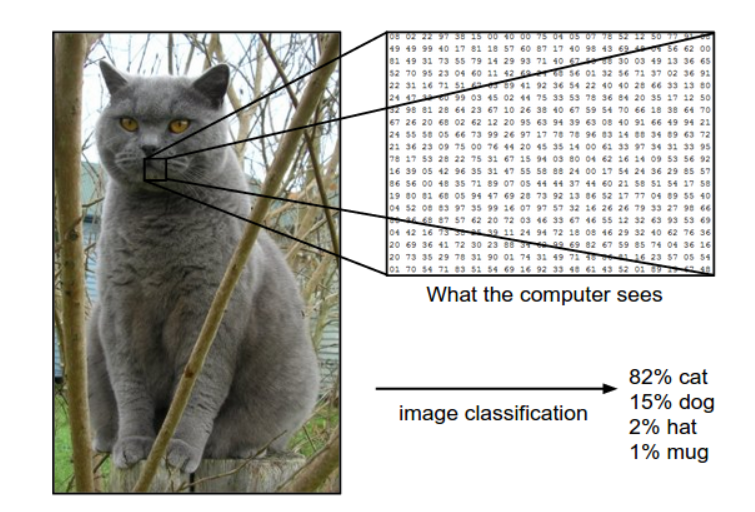
例子：以下图为例，图像分类模型读取该图片，并生成该图片属于集合 {cat, dog, hat, mug}中各个标签的概率。需要注意的是，对于计算机来说，图像是一个由数字组成的巨大的 3 维数组（在深度学习工具中，图像就是一个三维张量）。在下图这个例子中，猫的图像大小是宽 248 像素，高 400 像素，有 3 个颜色通道，分别是红、绿和蓝（简称 RGB）。

如此，该图像就包含了 \(248\times400\times3 = 297600\) 个数字，每个数字都是在范围 0-255 之间的整型，其中 0 表示全黑，255 表示全白。我们的任务就是把这些上百万的数字变成一个简单的标签，比如 "猫"。或者说，我们需要借助某种方法将这个原始数字网络转变为相应的有意义的语义——比如说“猫”标签

困难和挑战¶

对于人来说，识别出一个像 "猫" 一样视觉概念是简单至极的，然而从计算机视觉算法的角度来看就值得深思了。我们在下面列举了计算机视觉算法在图像识别方面遇到的一些困难

视角变化（ Viewpoint variation ）：同一个物体，摄像机可以从 多个角度来展现，尽管可能角度的变化很轻微，但是可能使得这些数字发生不直观的某种改变
类内差异（ Intra-class variation ）：一类物体的个体之间的外形差异很大，比如椅子。这一类物体有许多不同的对象，每个都有自己的外形。比如说猫就是一种很会变形的生物
相似类（ Fine-Grained Categories ）：不同类物体的个体之间的外形差异小
背景干扰（ Background clutter ）：物体可能 混入背景之中，使之难以被辨认
光照条件（ Illumination conditions ）：在像素层面上，光照的影响非常大，比如说 光照和昏暗情况 下图像会有不同情况
形变（ Deformation ）：很多东西的形状并非一成不变，会有很大变化。
遮挡（ Occlusion ）：目标物体可能被挡住。有时候只有物体的一小部分（可以小到几个像素）是可见的，比如说猫隐藏在草丛中，并不明显
大小变化（ Scale variation ）：物体可视的大小通常是会变化的（不仅是在图片中，在真实世界中大小也是变化的）。

面对以上所有变化及其组合，好的图像分类模型能够在维持分类结论稳定的同时，保持对 类内差异 足够敏感。

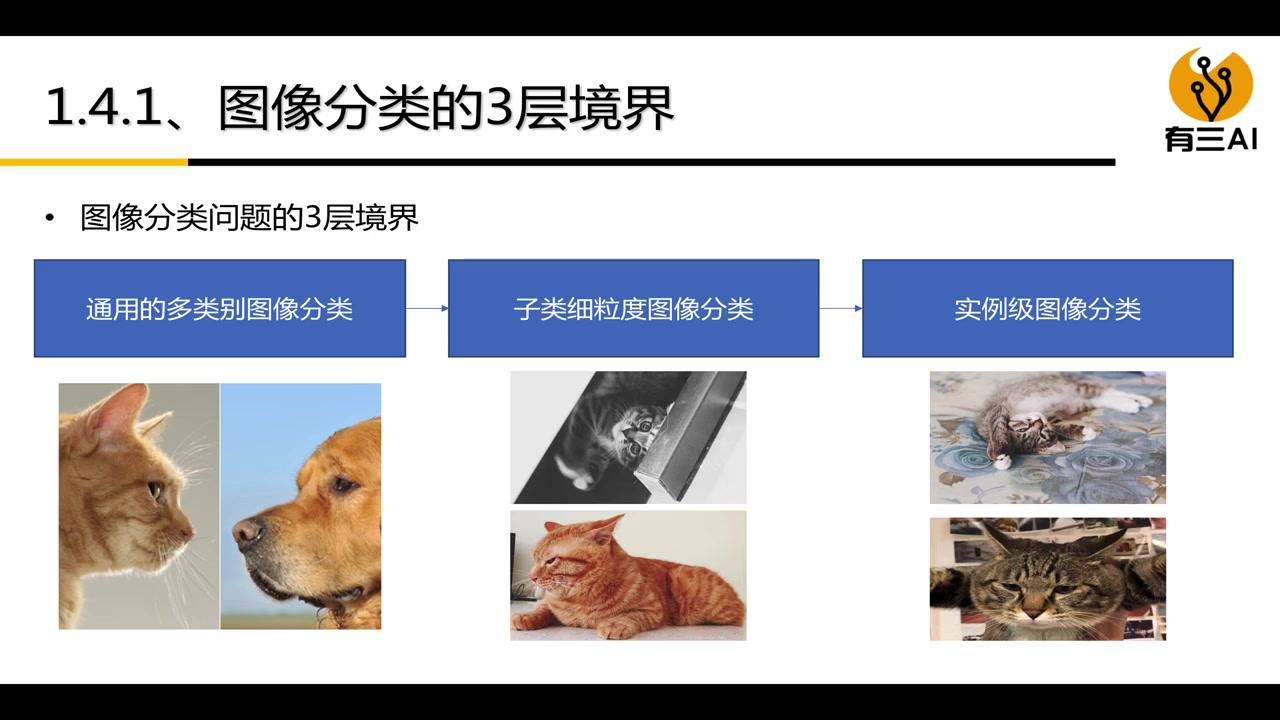
当然，图像分类有不同的境界

通用的多类别分类，是在不同物种的层次上进行分类，比如说我们只需要区分出猫和狗即可

子类细粒度分类是对一个大类中的子类进行划分，比如说我们区分了猫狗，我们需要进一步区别是什么品种的猫和狗

最高的是实例级分类，一个个体就是一个类，这种的细粒度最高

类别不平衡问题¶

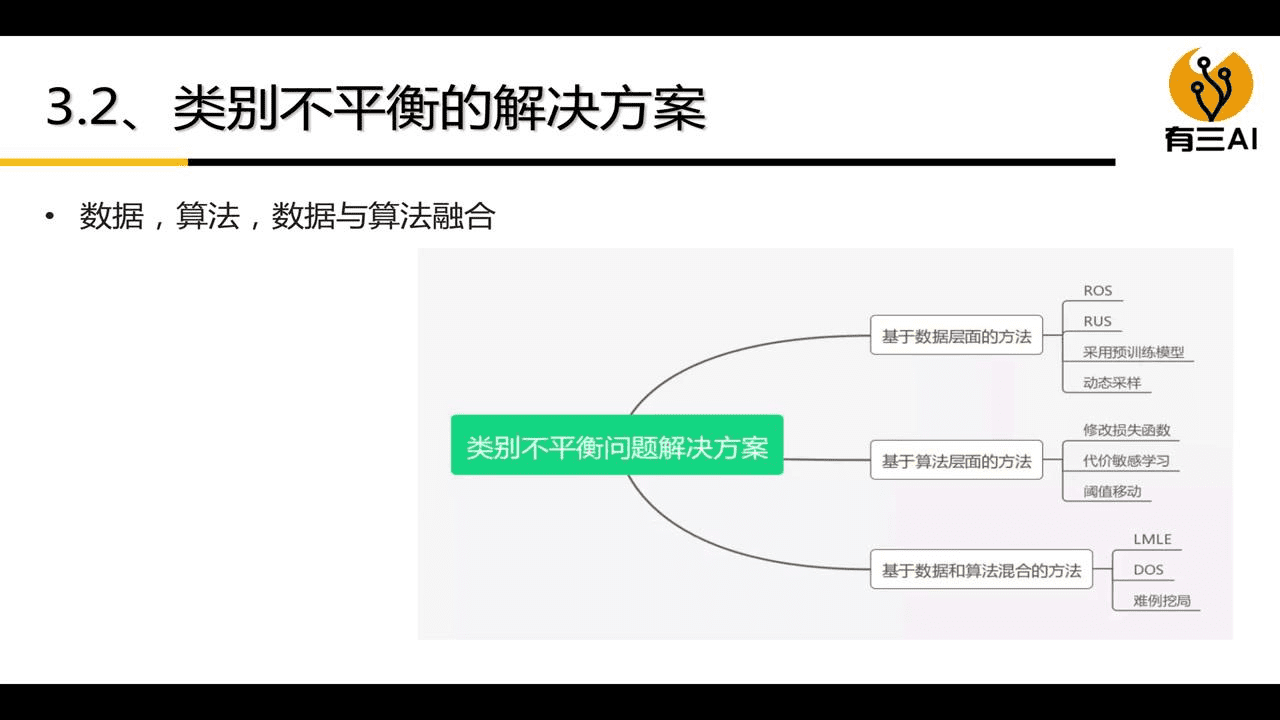
如果不同类别下样本数量相差很大，就会导致分类模型的性能变差，就与学生极度偏科一样，总分无法特别高，我们可以使用不同方面的方法提供解决方案

样本数量少问题¶

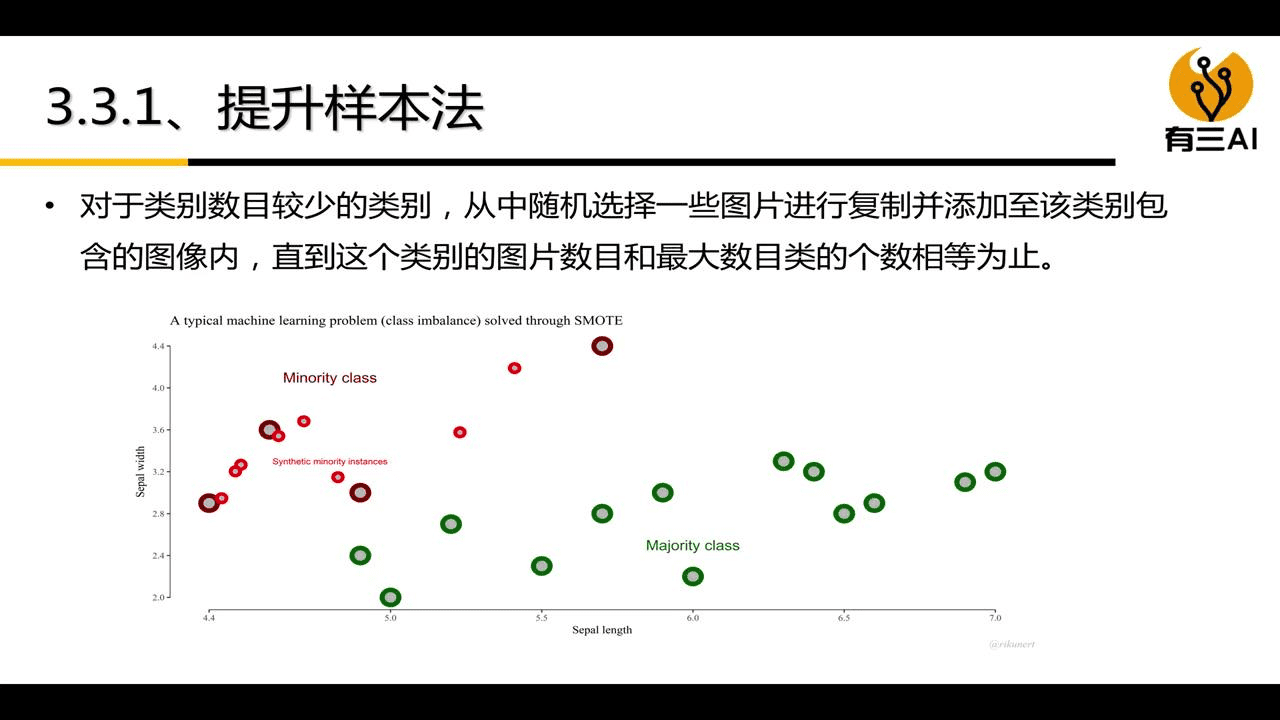
我们可以将样本数量很少的类别，随机进行一些插值，比如说随机选择一些图片进行复制添加到该类别包含的图像内，实际上这就是一种插值方式

当然我们可以以结果为导向进行提高，删除一些分类好的类别的样本，复制一些比较差的样本的类别

或者我们可以对算法本身进行改进，先构建一个比较均衡的数据集，然后在这个上面进行预训练，后面进行微调，也可以有一定程度上的提高

也可以进行基于样本数量的自适应加权，提高数量少的类别的权重

研究类别数量不均衡的问题是有意义的，因为在一些特定样本难以获取的任务上，样本数量几乎是必定极为不均衡的，比如说医疗视觉模型任务中，一些罕见病的影像数量很少

当然，我们也可以尝试通过迁移学习解决，如果预训练模型的训练数据足够大，并且与本任务相匹配，那么这个预训练模型所学的特征就会具有一定的通用性，比如说用途广泛的 ImageNet 数据集

当然我们也可以使用数据增强方式，人为扩充数据集，这样子就可以一定程度上解决数据集的问题

目标检测任务¶

当然，计算机视觉不止有图像分类，还有另一个相关的任务——目标检测（object detection），这个任务我们需要将图像中的目标对象圈出来

结果证明，图像分类本来就是一个基础，可以用来构建更多更复杂的应用程序，比如说目标检测，根据图片生成 caption 注释（例如下图可以生成 man ride horse），等

想法：如何实现图像分类？

根据之前所了解到的方法，我们可能首先想到通过对照片进行 边缘检测(edge detection) 来提取特征，如何尝试找到角点或者其他类型的可解释模式，比如说猫有三角形尖耳朵，所以可以通过检测这方面的边缘信息，或者我们知道猫有胡须，所以我们可以提取胡须的边缘信息，我们根据这些信息来写一个算法来检测他们

当然，这并不是一个很好的方法，比如说会有没有胡须的猫，会有没有尖耳朵的猫，或者有时候边缘检测器会失效从而无法正常提交所需的边缘，而且这很难进行迁移——当我们可以成功识别猫的时候，如果我们想将其用到其他方面，比如说识别狗，那么之前的工作将毫无意义，所以我们需要找到一种具有可扩展性的算法

数据驱动方法 Data-Driven Approach¶

Collect a dataset of images and labels
Use machine learning to train a classifier
Evaluate the classifier on new images

3 个重要的环节：

input：输入是包含 N 个图像的集合，每个图像的标签是 K 种分类标签中的一种。这个集合称为训练集。
train：输入图像数据集以及相关标签集合，使用某种机器学习算法，返回统计模型
predict：让分类器来预测它未曾见过的图像的分类标签，并以此来评价分类器的质量。

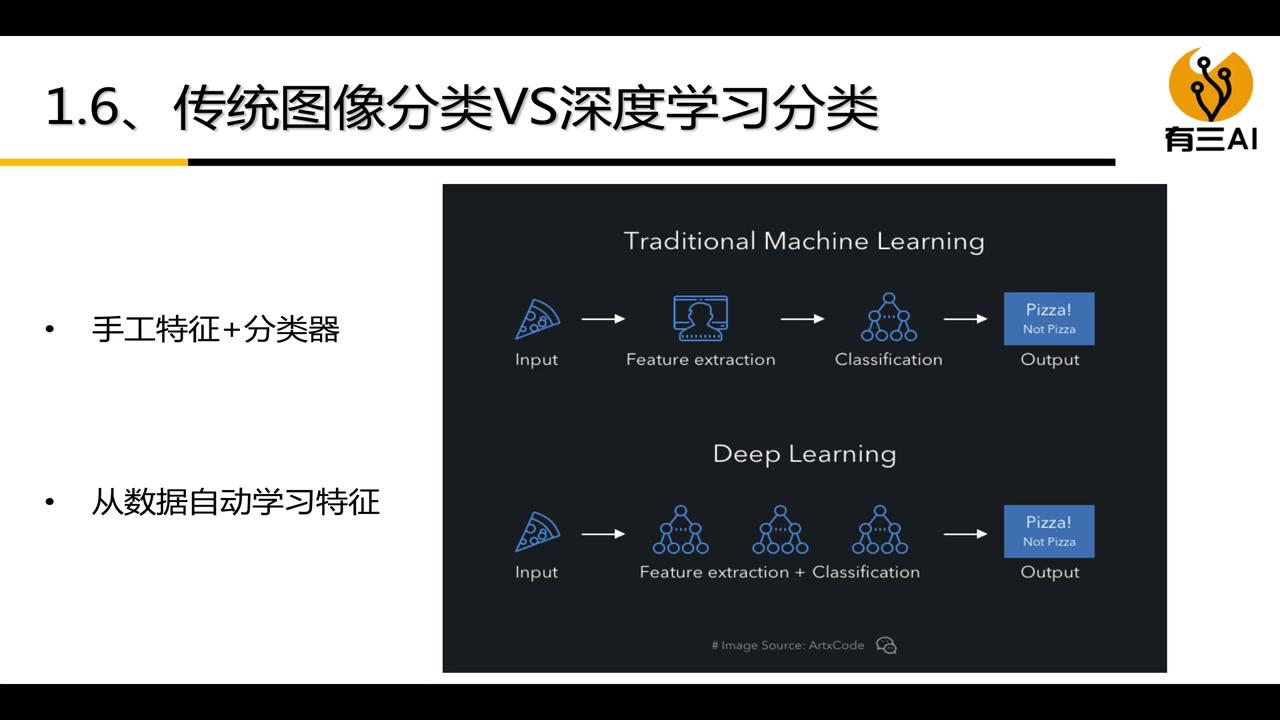
传统的图像分类是由专家去手动设计特征去提取（依靠人类现有的约定俗成的知识），深度学习分类方法则是让机器自动去学习如何提取特征和哪些提取特征，人类所需要做的就是投喂大量的目标 label 的图像。

如何写一个图像分类的算法呢？这和写个排序算法可是大不一样。怎么写一个从图像中认出猫的算法？搞不清楚。因此，与其在代码中直接写明各类物体到底看起来是什么样的，倒不如说我们采取的方法和教小孩儿看图识物类似：给计算机很多数据，然后实现学习算法，让计算机学习到每个类的外形。 这种方法，就是数据驱动方法。也就是使用拥有从数据中学习如何识别不同类型对象与图像的算法。既然该方法的第一步就是收集大量已经做好分类标注的图片来作为训练集，那么下面就看看数据集到底长什么样：

数据集¶

MNIST 数据集：计算机视觉中的果蝇¶

MNIST 数据集是一种手写数字数据集，其中的每张图片都包括一个不同的手写数字，大小统一为 28 \(\times\) 28，十个类别，有五万张作为训练集和一万张作为测试集

它更像一种玩具数据集，或者也被称为计算机视觉的果蝇，可以做很多测试，因为这个数据集很小而且简单，可以快速验证新想法

CIFAR 数据集¶

CIFAR-10：一个非常流行的图像分类数据集是 [CIFAR-10][15]。这个数据集包含了 60000 张 32X32 的小图像。每张图像都有 10 种分类标签中的一种并且只有一个主体对象。这 60000 张图像被分为包含 50000 张图像的训练集和包含 10000 张图像的测试集。可以视作 MNIST 的彩色增强版

在下图中你可以看见 10 个类的 10 张随机图片。

左边：从 [CIFAR-10][15] 数据库来的样本图像。右边：第一列是测试图像，然后第一列的每个测试图像右边是使用 Nearest Neighbor 算法，根据像素差异，从训练集中选出的 10 张最类似的图片。

此外还有 CIFAR100 数据集（100 类），细粒度更高，有一百个类，并且每五个类组成一个超类每个类有 600 个图像，并且每个图像有两个标签——一个是精细的类标签，一个是粗糙的超类标签，如下图所示

ImageNet：黄金数据集¶

这是一个非常大的数据，有两万种类别，同时有千万张图片（每个类别 1300 张），百万标注框，图像大小不统一，以其命名的 ImageNet 分类竞赛使用了其中一千个类的子集，在此竞赛中出现了大量经典工作，如 AlexNet 等

我们可以看到，一个图片的标注可以分为很多个级别，颗粒度越来越小（或者说一个图片有多个标签并且呈包含关系）

Nearest Neighbor 分类器¶

作为课程介绍的第一个方法，我们来实现一个 Nearest Neighbor 分类器。虽然这个分类器和卷积神经网络没有任何关系，实际中也极少使用而且其非常简单，但通过实现它，可以让读者对于解决图像分类问题的方法有个基本的认识，也就是机器学习系统的两个基本部分——训练、预测。

其中，训练函数，就是记住所有的数据和标签（或者说进行学习），预测函数，就是预测出图像最可能的标签

假设现在我们有 CIFAR-10 的 50000 张图片（每种分类 5000 张）作为训练集，我们希望将余下的 10000 作为测试集并给他们打上标签。Nearest Neighbor 算法将会拿着测试图片和训练集中每一张图片去比较，然后将它认为最相似的那个训练集图片的标签赋给这张测试图片。

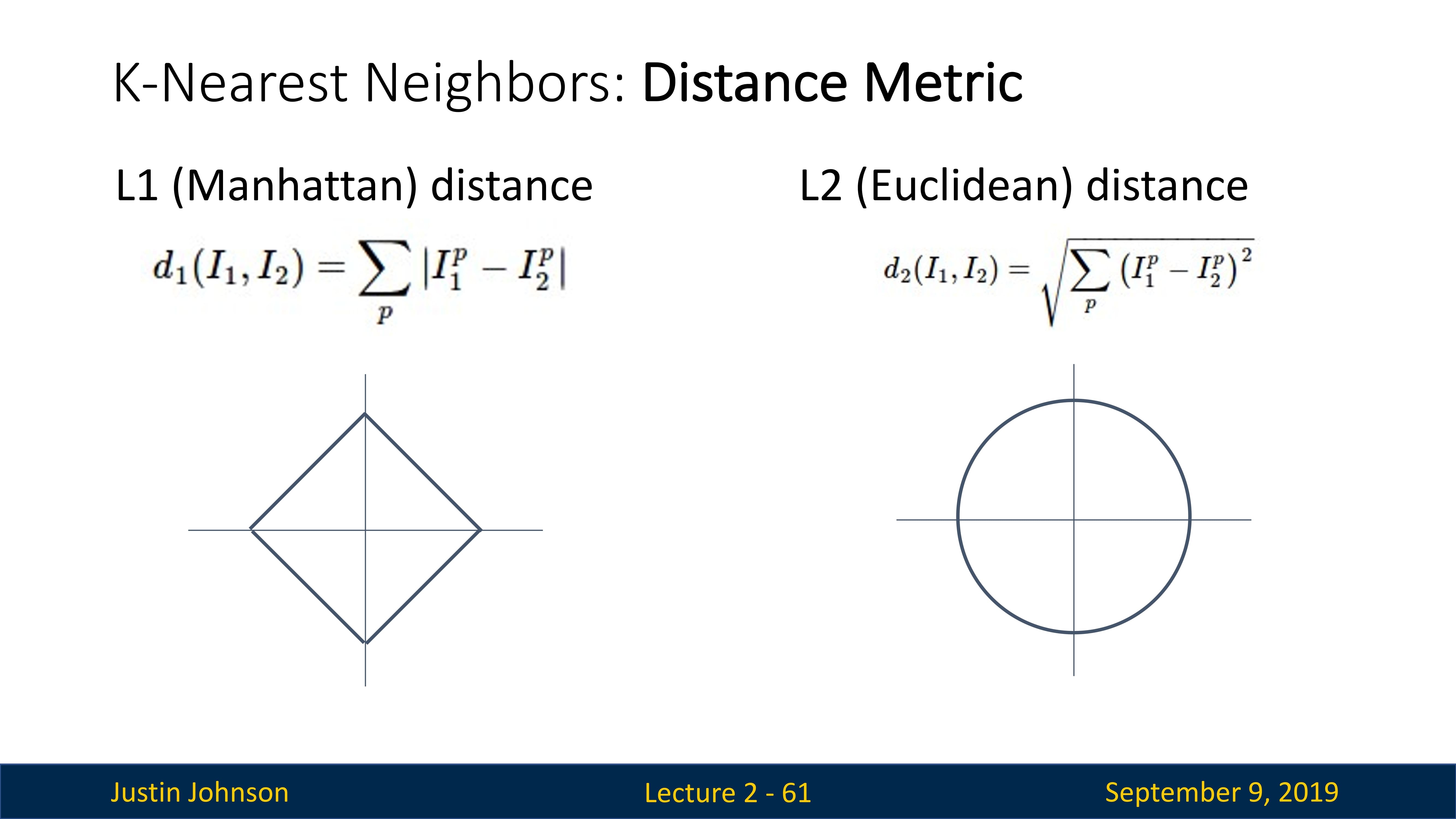
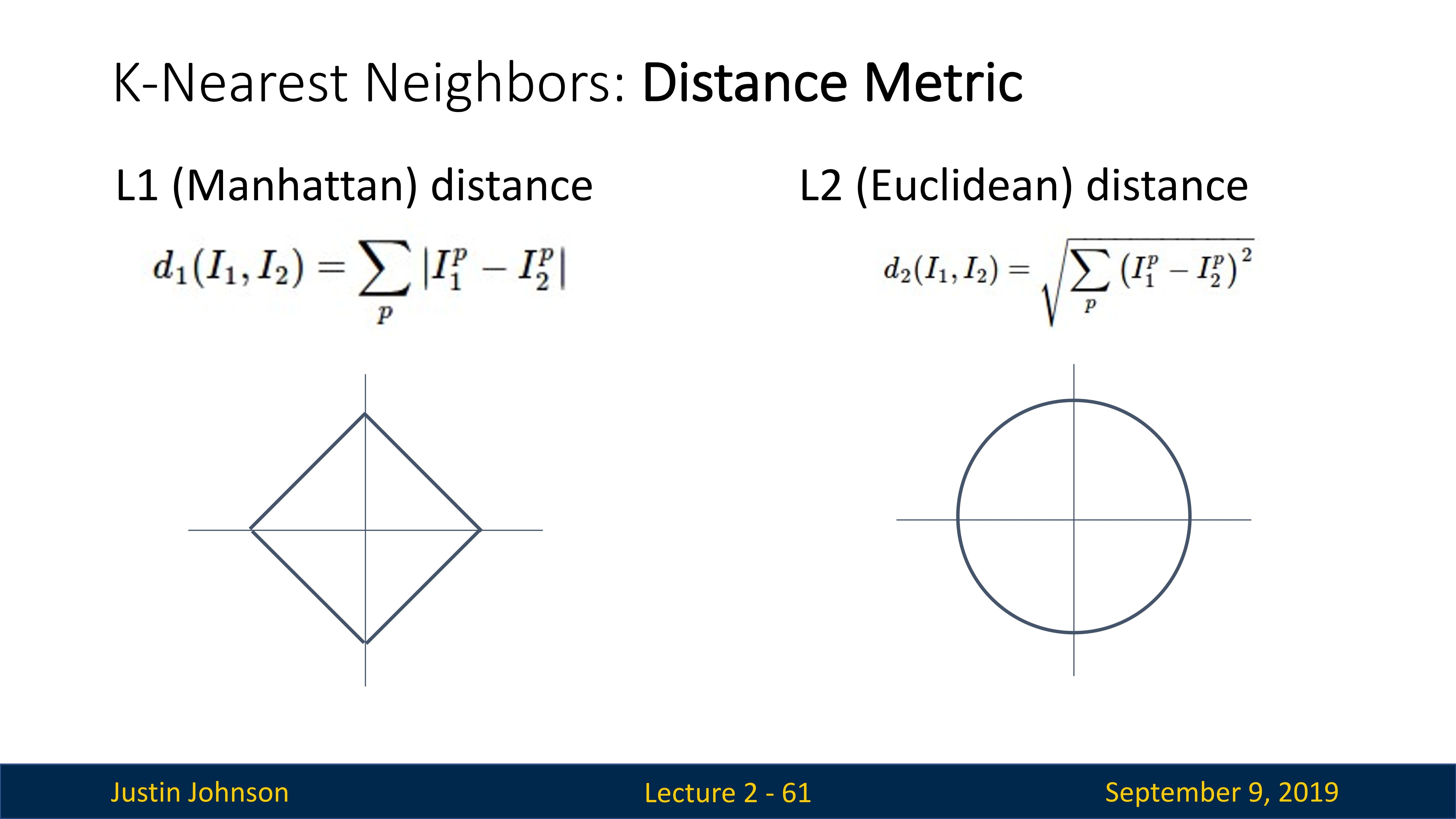
那么具体如何比较两张图片的相似程度呢（或者可以将相似程度理解为距离，距离越近，图片越相似）？在本例中，就是比较 32x32x3 的像素块。最简单的方法就是逐个像素比较，最后将差异值全部加起来。换句话说，就是将两张图片先转化为两个向量 \(I_1, I_2\)，然后计算他们的 L1 距离（曼哈顿距离）：

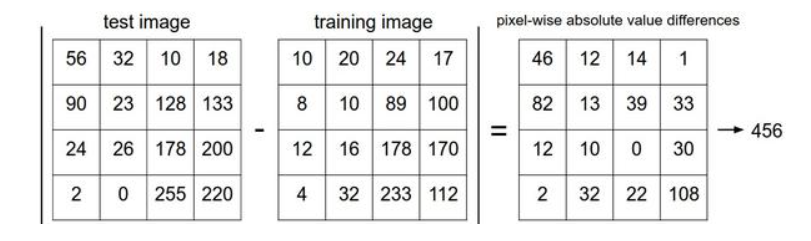
这里的求和是针对所有的像素。下面是整个比较流程的图例：

以图片中的一个颜色通道为例来进行说明。两张图片使用 L1 距离来进行比较。逐个像素求差值，然后将所有差值加起来得到一个数值。如果两张图片一模一样，那么 L1 距离为 0，但是如果两张图片很是不同，那 L1 值将会非常大。

下面，让我们看看如何用代码来实现这个分类器。首先，我们将 CIFAR-10 的数据加载到内存中，并分成 4 个数组：训练数据和标签，测试数据和标签。在下面的代码中，Xtr（大小是 \(50000\times32\times32\times3\)）存有训练集中所有的图像，Ytr 是对应的长度为 50000 的 1 维数组，存有图像对应的分类标签（从 0 到 9）：

Xtr, Ytr, Xte, Yte = load_CIFAR10('data/cifar10/') # a magifunction we provide
# flatten out all images to be one-dimensional
Xtr_rows = Xtr.reshape(Xtr.shape[0], 32 * 32 * 3) # Xtr_row becomes 50000 x 3072
Xte_rows = Xte.reshape(Xte.shape[0], 32 * 32 * 3) # Xte_row becomes 10000 x 3072

Xtr.shape[0] 获取 Xtr 数组的第一个维度的大小，即样本的数量。
reshape 方法用于将每个 32x32 的彩色图像（3 个通道分别对应 RGB）转换为一个 3072 维的 1 维向量（32 _ 32 _ 3 = 3072）。
Xtr_rows 和 Xte_rows 的形状分别为 (50000, 3072) 和 (10000, 3072)，其中每一行表示一个展平的图像。

通过 Xtr.shape[0]，你获得了样本数量（50000），并在 reshape 方法中将每张图像展平成一个 3072 维的向量。这样可以确保展平后的数组仍然包含 50000 个样本，每个样本有 3072 个特征。

现在我们得到所有的图像数据，并且把他们拉长成为行向量了。接下来展示如何训练并评价一个分类器：

    nn = NearestNeighbor() # create a Nearest Neighbor classifier class
    nn.train(Xtr_rows, Ytr) # train the classifier on the training images and labels
    Yte_predict = nn.predict(Xte_rows) # predict labels on the test images
    # and now print the classification accuracy, which is the average number
    # of examples that are correctly predicted (i.e. label matches)
    print 'accuracy: %f' % ( np.mean(Yte_predict == Yte) )

常见最近邻分类器

这里的 NearestNeighbor 是一个自定义的最近邻分类器类的实例化对象。这个类应该有方法来训练模型和进行预测

训练分类器

train() 方法将分类器训练在训练集上。它接收两个参数：

Xtr_rows：展平后的训练图像数据（50000 x 3072）。
Ytr：训练图像的标签。

在最近邻分类器中，训练通常只是将训练数据存储起来，因为预测时只需要找到距离最近的训练样本。

进行预测

predict() 方法使用最近邻算法对测试集 Xte_rows 进行预测。它将为测试集中的每个样本找到距离最近的训练样本，并返回相应的标签。

计算并打印了分类器在测试集上的准确率。

Yte_predict == Yte 会生成一个布尔数组，表示预测标签与实际标签是否匹配。

np.mean() 计算该布尔数组中 True 的比例（即分类正确的样本占比），作为准确率。

import numpy as np

class NearestNeighbor:
    def __init__(self):
        pass

    def train(self, X, y):
        # X 是形状为 N x D 的训练数据，其中每一行是一个示例，y 是 N 长度的一维标签数组
        # 最近邻分类器只需要记住所有的训练数据
        self.Xtr = X
        self.Ytr = y

    def predict(self, X):
        # X 是形状为 N x D 的测试数据，其中每一行是一个我们想预测标签的示例
        num_test = X.shape[0]
        # 确保输出类型与输入类型匹配
        Ypred = np.zeros(num_test, dtype=self.Ytr.dtype)

        # 遍历所有测试样本
        for i in range(num_test):
            # 找到与第 i 个测试样本最近的训练样本
            # 使用 L1 距离（绝对值差的和）
            distances = np.sum(np.abs(self.Xtr - X[i, :]), axis=1)
            # 获取距离最小的索引
            min_index = np.argmin(distances)
            # 预测最近样本的标签
            Ypred[i] = self.Ytr[min_index]

        return Ypred

如果你用这段代码跑 CIFAR-10，你会发现准确率能达到 38.6%。这比随机猜测的 10%要好，但是比人类识别的水平（[据研究推测是 94%__][21]）和卷积神经网络能达到的 95%还是差多了。点击查看基于 CIFAR-10 数据的[Kaggle 算法竞赛排行榜__][22]。

距离选择：计算向量间的距离有很多种方法，另一个常用的方法是 L2 距离，从几何学的角度，可以理解为它在计算两个向量间的欧式距离。L2 距离的公式如下：

换句话说，我们依旧是在计算像素间的差值，只是先求其平方，然后把这些平方全部加起来，最后对这个和开方。在 Numpy 中，我们只需要替换上面代码中的 1 行代码就行：

    distances = np.sqrt(np.sum(np.square(self.Xtr - X[i,:]), axis = 1))

注意在这里使用了 np.sqrt，但是在实际中可能不用。因为求平方根函数是一个单调函数，它对不同距离的绝对值求平方根虽然改变了数值大小，但依然保持了不同距离大小的顺序。所以用不用它，都能够对像素差异的大小进行正确比较。如果你在 CIFAR-10 上面跑这个模型，正确率是 35.4%，比刚才低了一点。

k-Nearest Neighbor 分类器¶

你可能注意到了，为什么只用最相似的 1 张图片的标签来作为测试图像的标签呢？这不是很奇怪吗！是的，使用 k-Nearest Neighbor 分类器 就能做得更好。它的思想很简单：与其只找最相近的那 1 个图片的标签，我们找最相似的 k 个图片的标签，然后让他们针对测试图片进行投票，最后把票数最高的标签作为对测试图片的预测。所以当 k = 1 的时候，k-Nearest Neighbor 分类器就是 Nearest Neighbor 分类器。从直观感受上就可以看到，更高的 k 值可以让分类的效果更平滑，使得分类器对于异常值更有抵抗力。

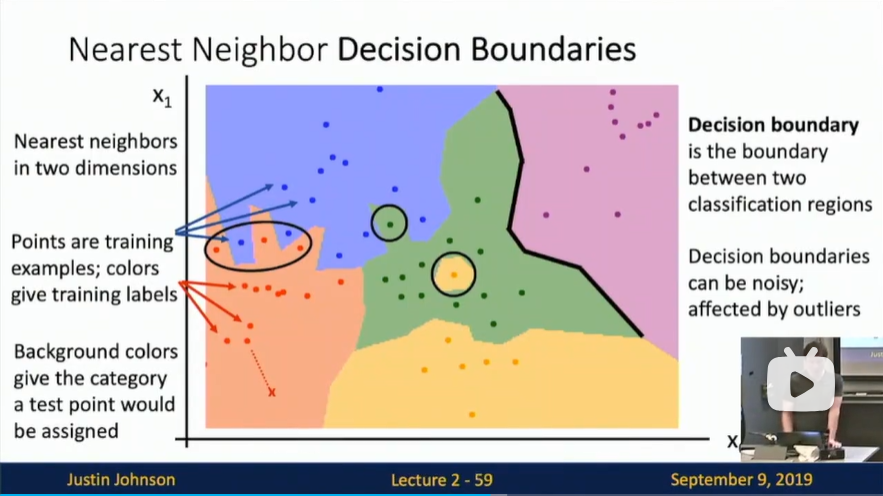
上面示例展示了 Nearest Neighbor 分类器和 5-Nearest Neighbor 分类器的区别。例子使用了 2 维的点来表示，分成 3 类（红、蓝和绿）。不同颜色区域代表的是使用 L2 距离的分类器的 决策边界。白色的区域是分类模糊的例子（即图像与两个以上的分类标签绑定）。需要注意的是，在 NN 分类器中，异常的数据点（比如：在蓝色区域中的绿点）制造出一个不正确预测的孤岛。5-NN 分类器将这些不规则都平滑了，使得它针对测试数据的 泛化（generalization） 能力更好（例子中未展示）。注意，5-NN 中也存在一些灰色区域，这些区域是因为近邻标签的最高票数相同导致的（比如：2 个邻居是红色，2 个邻居是蓝色，还有 1 个是绿色)。

用于超参数调优的验证集¶

k-NN 分类器需要设定 k 值，那么选择哪个 k 值最合适的呢？我们可以选择不同的距离函数，比如 L1 范数和 L2 范数等，那么选哪个好？还有不少选择我们甚至连考虑都没有考虑到（比如：点积）。所有这些选择，被称为 超参数（hyperparameter）。在基于数据进行学习的机器学习算法设计中，超参数是很常见的。一般说来，这些超参数具体怎么设置或取值并不是显而易见的。

你可能会建议尝试不同的值，看哪个值表现最好就选哪个。

choose hyperparameters that work best on the data

K = 1 always works perfectly on training data

Split data into train and test，choose hyperparameters that work best on the test data

No idea how algorithm will perform on new data

特别注意：决不能使用测试集来进行调优。当你在设计机器学习算法的时候，应该把测试集看做非常珍贵的资源，不到最后一步，绝不使用它。如果你使用测试集来调优，而且算法看起来效果不错，那么真正的危险在于：算法实际部署后，性能可能会远低于预期。这种情况，称之为算法对测试集 过拟合。从另一个角度来说，如果使用测试集来调优，实际上就是把测试集当做训练集，由测试集训练出来的算法再跑测试集，自然性能看起来会很好。这其实是过于乐观了，实际部署起来效果就会差很多。所以，最终测试的时候再使用测试集，可以很好地近似度量你所设计的分类器的泛化性能（在接下来的课程中会有很多关于泛化性能的讨论）。

测试数据集只使用一次，即在训练完成后评价最终的模型时使用。

但是只有训练集和测试集会有一个问题，那就是不知道算法在新数据上表现如何。解决思路是：从训练集中取出一部分数据用来调优，我们称之为验证集（validation set）。 以 CIFAR-10 为例，我们可以用 49000 个图像作为训练集，用 1000 个图像作为验证集。验证集其实就是作为假的测试集来调优

下面就是代码：

    # assume we have Xtr_rows, Ytr, Xte_rows, Yte as before
    # recall Xtr_rows is 50,000 x 3072 matrix
    Xval_rows = Xtr_rows[:1000, :] # take first 1000 for validation
    Yval = Ytr[:1000]
    Xtr_rows = Xtr_rows[1000:, :] # keep last 49,000 for train
    Ytr = Ytr[1000:]

    # find hyperparameters that work best on the validation set
    validation_accuracies = []
    for k in [1, 3, 5, 10, 20, 50, 100]:

      # use a particular value of k and evaluation on validation data
      nn = NearestNeighbor()
      nn.train(Xtr_rows, Ytr)
      # here we assume a modified NearestNeighbor class that can take a k as input
      Yval_predict = nn.predict(Xval_rows, k = k)
      acc = np.mean(Yval_predict == Yval)
      print 'accuracy: %f' % (acc,)

      # keep track of what works on the validation set
      validation_accuracies.append((k, acc))

程序结束后，我们会作图分析出哪个 k 值表现最好，然后用这个 k 值来跑真正的测试集，并作出对算法的评价。把训练集分成训练集和验证集。使用验证集来对所有超参数调优。最后只在测试集上跑一次并报告结果。

交叉验证。有时候，训练集数量较小（因此验证集的数量更小），人们会使用一种被称为 交叉验证 的方法，这种方法更加复杂些。还是用刚才的例子，如果是交叉验证集，我们就不是取 1000 个图像，而是将训练集平均分成 5 份，其中 4 份用来训练，1 份用来验证。然后我们循环着取其中 4 份来训练，其中 1 份来验证，最后取所有 5 次验证结果的平均值作为算法验证结果。

常用的数据分割模式。给出训练集和测试集后，训练集一般会被均分。这里是分成 5 份。前面 4 份用来训练，黄色那份用作验证集调优。如果采取交叉验证，那就各份轮流作为验证集。最后模型训练完毕，超参数都定好了，让模型跑一次（而且只跑一次)测试集，以此测试结果评价算法。

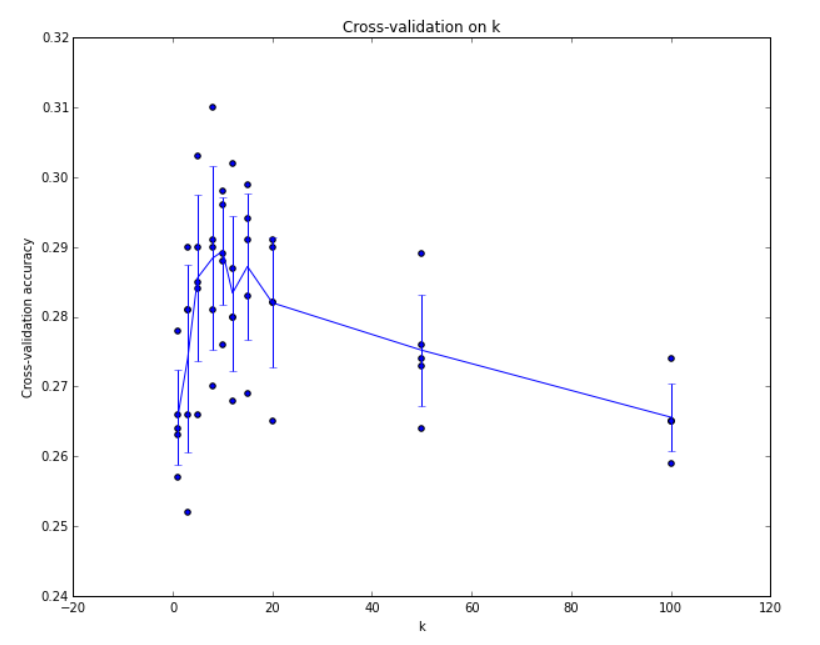
这就是 5 份交叉验证对 k 值调优的例子。针对每个 k 值，得到 5 个准确率结果，取其平均值，然后对不同 k 值的平均表现画线连接。本例中，当 k = 7 的时算法表现最好（对应图中的准确率峰值）。如果我们将训练集分成更多份数，直线一般会更加平滑（噪音更少）。

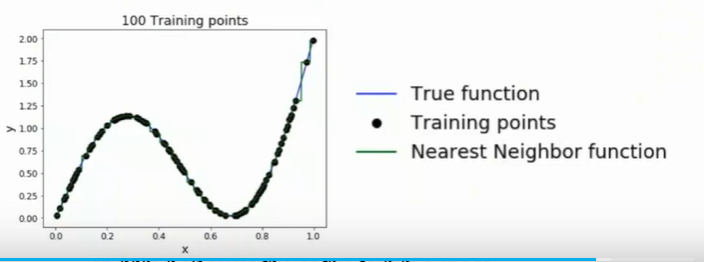
随着 training samples 的数量趋于无穷，nearest neighbor 可以表示任何函数

但是随着维数的增长，为了尽可能覆盖测试集，测试点的数量指数级增长

Nearest Neighbor 分类器的优劣¶

现在对 Nearest Neighbor 分类器的优缺点进行思考。首先，Nearest Neighbor 分类器易于理解，实现简单。其次，算法的训练不需要花时间，因为其训练过程只是将训练集数据存储起来。然而测试要花费大量时间计算，因为每个测试图像需要和所有存储的训练图像进行比较，这显然是一个缺点。在实际应用中，我们关注测试效率远远高于训练效率。

其实，我们后续要学习的 卷积神经网络 在这个权衡上走到了另一个极端：虽然训练花费很多时间，但是一旦训练完成，对新的测试数据进行分类非常快。这样的模式就符合实际使用需求。

Nearest Neighbor 分类器的计算复杂度研究是一个活跃的研究领域，若干 Approximate Nearest Neighbor (ANN)算法和库的使用可以提升 Nearest Neighbor 分类器在数据上的计算速度（比如：[FLANN__][14]）。这些算法可以在准确率和时空复杂度之间进行权衡，并通常依赖一个预处理/索引过程，这个过程中一般包含 kd 树的创建和 k-means 算法的运用。

Nearest Neighbor 分类器在某些特定情况（比如数据维度较低）下，可能是不错的选择。但是在实际的图像分类工作中，很少使用。

图像都是高维度数据（他们通常包含很多像素），要想性能好，训练集指数增长需要足够庞大
测试时间过于漫长
而高维度向量之间的距离通常是反直觉的。下面的图片展示了基于像素的相似和基于感官的相似是有很大不同的：

在高维度数据上，基于像素的的距离和感官上的非常不同。上图中，右边 3 张图片和左边第 1 张原始图片的 L2 距离是一样的。很显然，基于像素比较的相似和感官上以及语义上的相似是不同的。

小结¶

介绍了 图像分类 问题。在该问题中，给出一个由被标注了分类标签的图像组成的集合，要求算法能预测没有标签的图像的分类标签，并根据算法预测准确率进行评价。
介绍了一个简单的图像分类器：最近邻分类器(Nearest Neighbor classifier)。分类器中存在不同的超参数(比如 k 值或距离类型的选取)，要想选取好的超参数不是一件轻而易举的事。
选取超参数的正确方法是：将原始训练集分为训练集和 验证集，我们在验证集上尝试不同的超参数，最后保留表现最好那个。
如果训练数据量不够，使用 交叉验证 方法，它能帮助我们在选取最优超参数的时候减少噪音。
一旦找到最优的超参数，就让算法以该参数在测试集跑且只跑一次，并根据测试结果评价算法。
最近邻分类器能够在 CIFAR-10 上得到将近 40%的准确率。该算法简单易实现，但需要存储所有训练数据，并且在测试的时候过于耗费计算能力。
最后，我们知道了仅仅使用 L1 和 L2 范数来进行像素比较是不够的，图像更多的是按照背景和颜色被分类，而不是语义主体分身。

在接下来的课程中，我们将专注于解决这些问题和挑战，并最终能够得到超过 90%准确率的解决方案。该方案能够在完成学习就丢掉训练集，并在一毫秒之内就完成一张图片的分类。

小结：实际应用 k-NN¶

如果你希望将 k-NN 分类器用到实处（最好别用到图像上，若是仅仅作为练手还可以接受），那么可以按照以下流程：

预处理你的数据：对你数据中的特征进行归一化（normalize），让其具有零平均值（zero mean）和单位方差（unit variance）。在后面的小节我们会讨论这些细节。本小节不讨论，是因为图像中的像素都是同质的，不会表现出较大的差异分布，也就不需要标准化处理了。
如果数据是高维数据，考虑使用降维方法，比如 PCA([wiki ref __][18], [CS229ref__][19], [blog ref __][20])或[随机投影__][21]。
将数据随机分入训练集和验证集。按照一般规律，70%-90% 数据作为训练集。这个比例根据算法中有多少超参数，以及这些超参数对于算法的预期影响来决定。如果需要预测的超参数很多，那么就应该使用更大的验证集来有效地估计它们。如果担心验证集数量不够，那么就尝试交叉验证方法。如果计算资源足够，使用交叉验证总是更加安全的（份数越多，效果越好，也更耗费计算资源）。
在验证集上调优，尝试足够多的 k 值，尝试 L1 和 L2 两种范数计算方式。
如果分类器跑得太慢，尝试使用 Approximate Nearest Neighbor 库（比如[FLANN__][14]）来加速这个过程，其代价是降低一些准确率。
对最优的超参数做记录。记录最优参数后，是否应该让使用最优参数的算法在完整的训练集上运行并再次训练呢？因为如果把验证集重新放回到训练集中（自然训练集的数据量就又变大了），有可能最优参数又会有所变化。在实践中，不要这样做。千万不要在最终的分类器中使用验证集数据，这样做会破坏对于最优参数的估计。直接使用测试集来测试用最优参数设置好的最优模型，得到测试集数据的分类准确率，并以此作为你的 kNN 分类器在该数据上的性能表现。

评价指标¶

正负样本¶

指标首先是统计正负样本

正样本（Positive Samples）：
正样本是指那些标签或输出是正类的数据点。在二元分类中，“正”通常意味着我们感兴趣的类别，或者是我们希望模型检测或预测的类别。
例如，在垃圾邮件检测问题中，垃圾邮件是正样本，因为模型的任务是识别出垃圾邮件。
负样本（Negative Samples）：
负样本是指那些标签或输出是负类的数据点。在二元分类中，“负”通常意味着非目标类别，即我们不希望模型检测或预测的类别。
在垃圾邮件检测的例子中，非垃圾邮件是负样本。

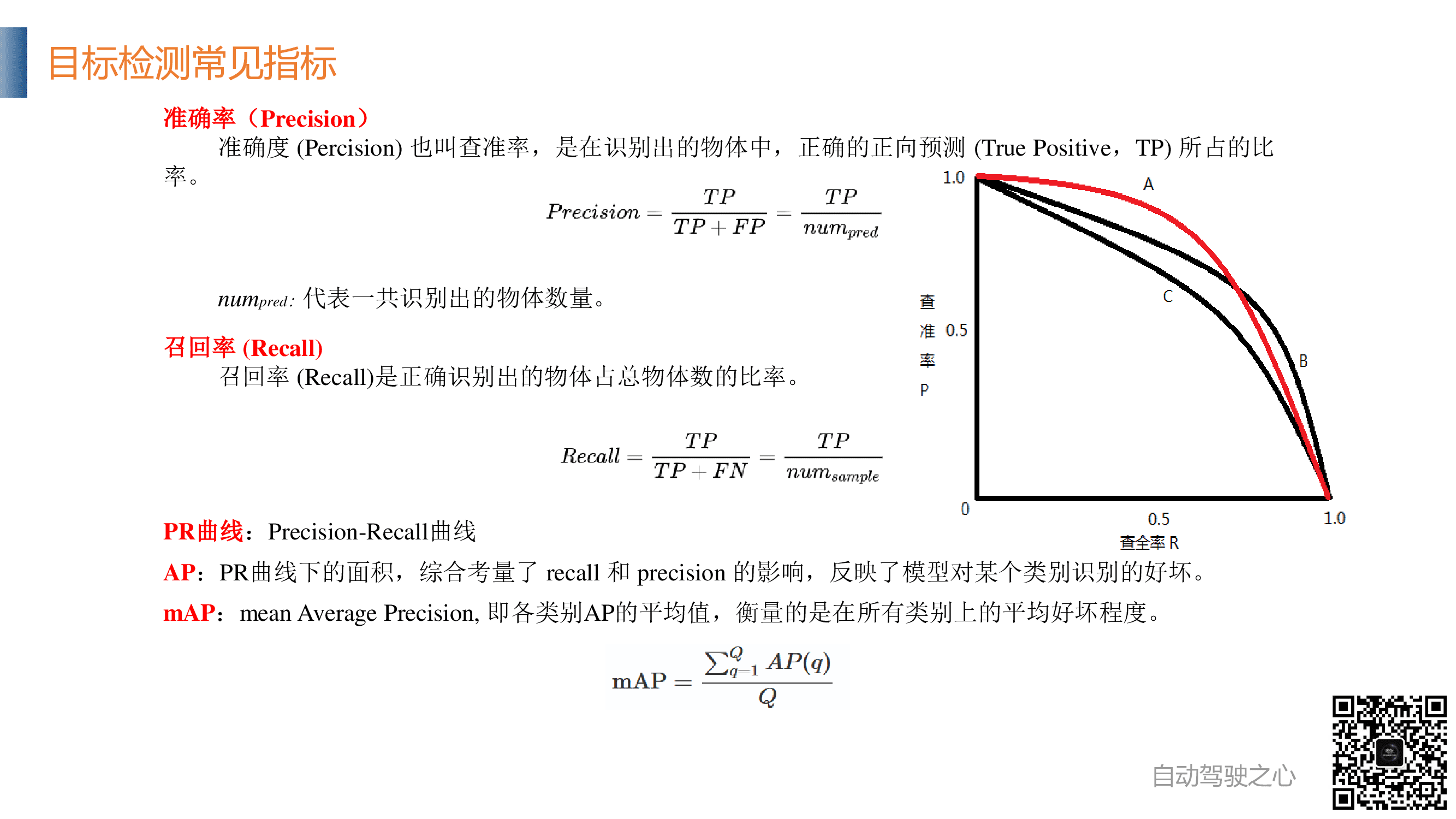
PR 曲线¶

Precision：也叫查准率，表示所有被模型判定为正样本中，真正的正样本的比例。
Recall：也叫查全率或者召回率，表示所有真正的正样本中，被模型判定为正样本的比例。

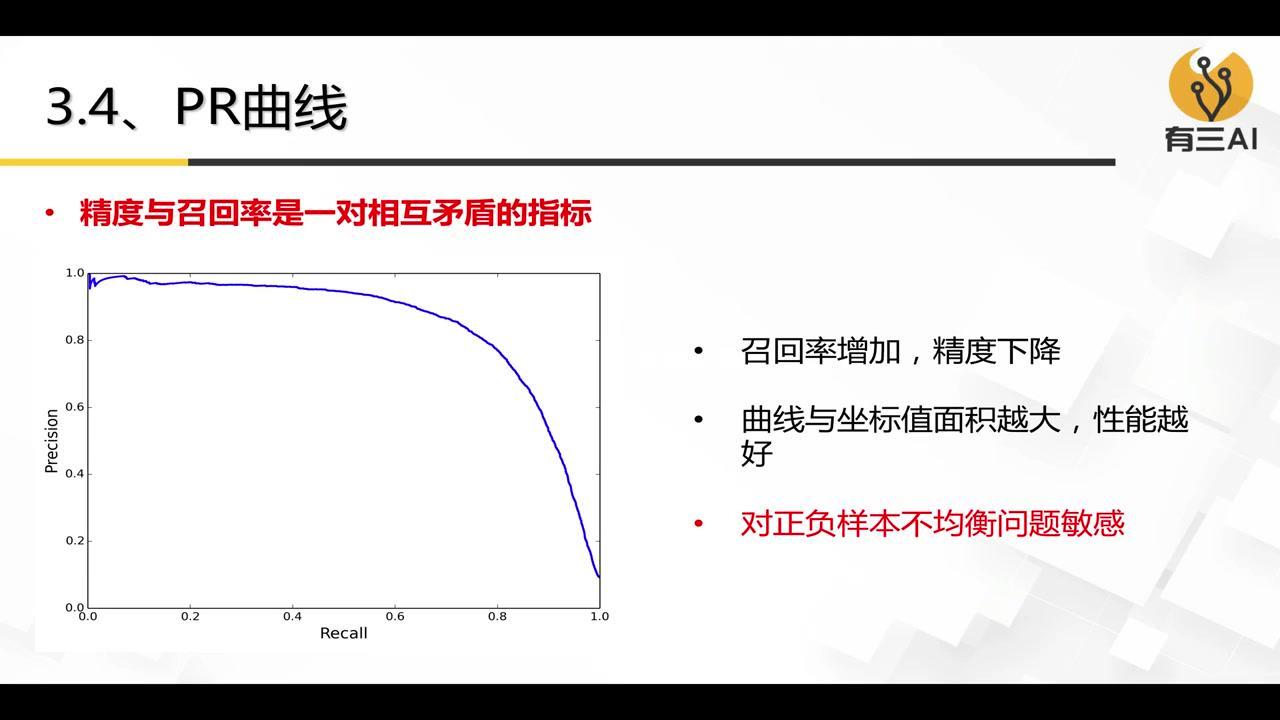
通常会为每个物体类别绘制一个 PR 曲线（Precision-Recall 曲线），然后计算该曲线下的面积，即 AP（Average Precision，平均精度）。AP 值越高，说明模型在该类别的检测性能越好。

不过精度和召回率是相互矛盾的，召回率越高，模型越倾向于把更多样本归类为正样本，就容易误判

所以我们需要综合考虑，也就是 PR 曲线的面积越大，性能就越好，但是 PR 曲线对正负样本不均衡很敏感，PR 曲线更关注正样本的预测准确性，因此在正样本较少的情况下，模型性能的微小变化也会在 PR 曲线上表现得非常明显。

所以我们也会使用 ROC 曲线进行更全面的判断

ROC 曲线与 AUC¶

AUC 就是 ROC 曲线下的面积，AUC 曲线对正负样本不平衡的敏感度较低。即使在负样本数量远超正样本的情况下，AUC 仍能提供较为合理的性能评估。这是因为 AUC 考虑了所有可能的分类阈值，并且 FPR 的计算抵消了负样本数量多的影响。

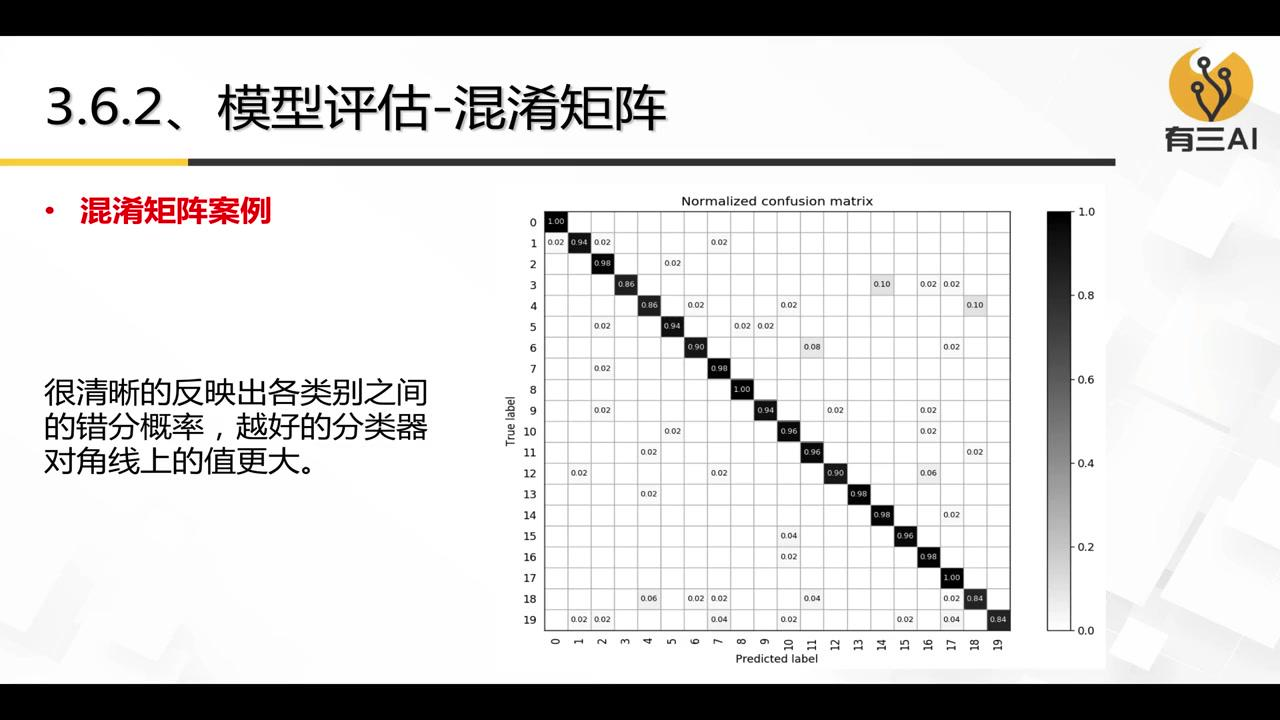
混淆矩阵¶

对于多分类问题，比如说有 K 类，就有一个 KxK 的混淆矩阵，元素 \(c_{ij}\) 表示第 i 类样本被分类器判定为第 j 类的数量，主对角线是正确分类的样本数量，我们可以通过观察混淆矩阵，判断哪些类更容易混淆