Linear_Classifier

约 9930 个字 57 行代码 预计阅读时间 50 分钟

概述

上一篇笔记介绍了图像分类问题。图像分类的任务，就是从已有的固定分类标签集合中选择一个并分配给一张图像。我们还介绍了k-Nearest Neighbor （k-NN）分类器，该分类器的基本思想是通过将测试图像与训练集带标签的图像进行比较，来给测试图像打上分类标签。

k-Nearest Neighbor 分类器存在以下不足：

• 分类器必须记住所有训练数据并将其存储起来，以便于未来测试数据用于比较。这在存储空间上是低效的，因为数据集的大小很容易就以 GB 计算。
• 对一个测试图像进行分类需要 和所有训练图像作比较，算法计算资源耗费高。

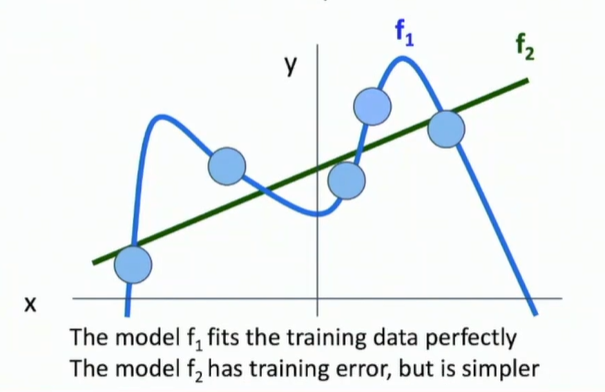
所有我们使用了一种更广泛的构建机器学习模型的方法，那就是参数方法，这种方法的想法是 参数可学习（parametric approach）

概述：我们将要实现一种更强大的方法来解决图像分类问题，该方法可以自然地延伸到神经网络和卷积神经网络上。这种方法主要有两部分组成：

一个是评分函数（score function），它是原始图像数据到类别分值的映射。

另一个是损失函数（loss function），它是用来量化预测分类标签的得分与真实标签之间一致性的。

该方法可转化为一个最优化问题，在最优化过程中，将通过更新评分函数的参数来最小化损失函数值。

从图像到标签分值的参数化映射

该方法的第一部分就是定义一个评分函数 score function，这个函数将图像的像素值映射为各个分类类别的得分，得分高低代表图像属于该类别的可能性高低。

下面会利用一个具体例子来展示该方法。现在假设有一个包含很多图像的训练集\(x_{i}\in R^{D}\)，每个图像都有一个对应的分类标签\(y_{i}\)。这里\(i=1,2,3...N\)并且\(y_{i}\in 1...K\)。这就是说，我们有 N 个图像样例，每个图像的维度是 D，共有 K 种不同的分类。

举例来说，在 CIFAR-10 中，我们有一个 N = 50000 的训练集，每个图像有\(D=32\times32\times3=3072\)个像素，而 K = 10，这是因为图片被分为 10 个不同的类别（狗，猫，汽车等）。我们现在定义评分函数为：\(f:R^{D}\rightarrow R^{K}\)，该函数是原始图像像素到分类分值的映射。

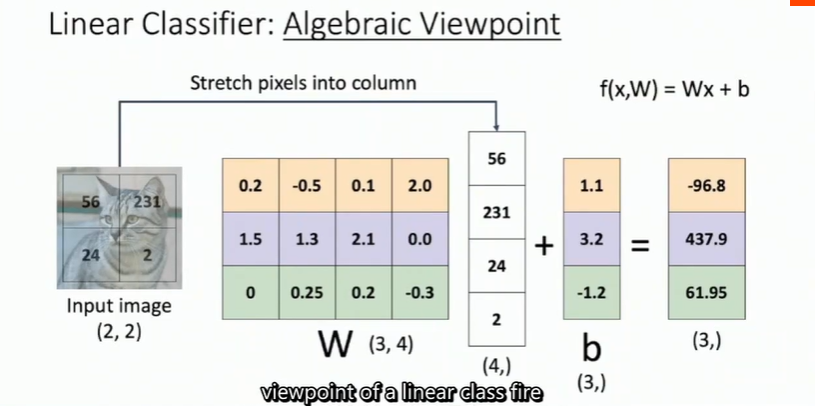
线性分类器：在本模型中，我们从最简单的概率函数开始，一个线性映射：

\[f(x_{i},W,b)=Wx_{i}+b\]

在上面的公式中，假设每个图像数据都被拉长为一个长度为 D 的列向量，大小为 [D x 1]。其中大小为\([K \times D]\)的矩阵 W 和大小为 [K x 1] 列向量 b 为该函数的 参数（parameters）。

以 CIFAR-10 为例，第 i 个图像的所有像素信息被拉成为一个 [3072 x 1] 的列向量，W 大小为 [10x3072]，b 的大小为 [10x1]。因此，3072 个数字（原始像素数值）输入函数，函数输出 10 个数字（不同分类得到的分值）。参数 W 被称为 权重（weights）。b 被称为 偏差向量（bias vector）

需要注意的几点：

• 一个单独的矩阵乘法\(W{x_{i}}\)就高效地并行评估 10 个不同的分类器（每个分类器针对一个分类），其中每个类的分类器就是 W 的一个行向量。

• 输入数据\((x_{i},y_{i})\)是给定且不可改变的，但参数W和b是可控制改变的。我们的目标就是通过设置这些参数，使得计算出来的分类分值情况和训练集中图像数据的真实类别标签相符。

• 优势：

• 训练数据是用来学习到参数 W 和 b 的，一旦训练完成，训练数据就可以丢弃，留下学习到的参数即可

• 只需要做一个矩阵乘法和一个矩阵加法就能对一个测试数据分类，这比 k-NN 中将测试图像和所有训练数据做比较的方法快

• 可以将偏差 b 作为一个单独的可学习参数，我们也可以进行合并，将其合并到权重矩阵之中，这样的方式无非就是给权重矩阵扩张一下列向量，并且给输入向量增加一个常量维度

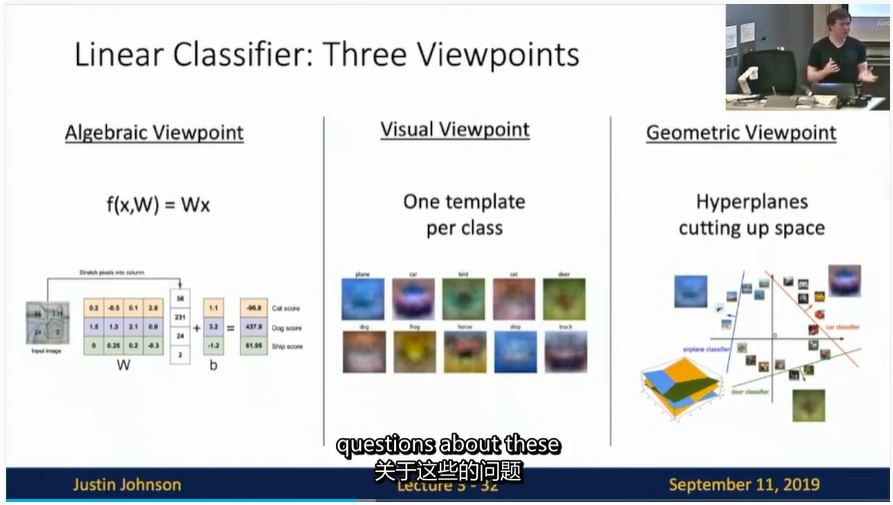
理解线性分类器

1. 线性分类器计算图像中 3 个颜色通道中所有像素的值与权重的矩阵乘，从而得到分类分值。根据我们对权重设置的值，对于图像中的某些位置的某些颜色，函数表现出喜好或者厌恶（根据每个权重的符号而定）。

举个例子，可以想象 "船" 分类就是被大量的蓝色所包围（对应的就是水）。那么 "船" 分类器在蓝色通道上的权重就有很多的正权重（它们的出现提高了 "船" 分类的分值），而在绿色和红色通道上的权重为负的就比较多（它们的出现降低了 "船" 分类的分值）。

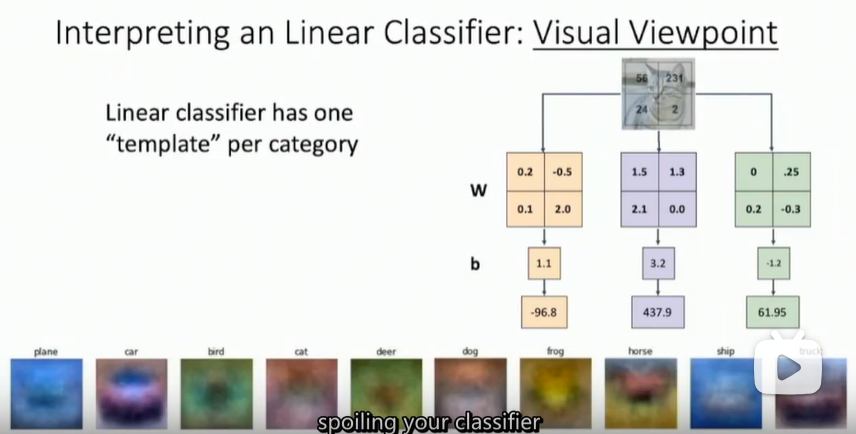
1. 线性分类器可以理解为对于每一个 category，生成一个类模板。此时不再将图像数据拉伸为列向量，相应的改变权重矩阵适应图像数据的维数。改变后的权重矩阵类似于模板，后续就是计算内积，进行模板的匹配。

从另一个角度来看，可以认为还是在高效地使用 k-NN，不同的是我们没有使用所有的训练集的图像来比较 ，而是每个类别只用了一张图片（这张图片是我们学习到的，而不是训练集中的某一张），而且我们会使用内积来计算向量间的距离，而不是使用 L1 或者 L2 距离。

• 船的模板如期望的那样有很多蓝色像素。如果图像是一艘船行驶在大海上，那么这个模板利用内积计算图像将给出很高的分数。
• 可以看到马的模板看起来似乎是两个头的马，这是因为训练集中的马的图像中马头朝向各有左右造成的。线性分类器将这两种情况融合到一起了。类似的，汽车的模板看起来也是将几个不同的模型融合到了一个模板中，并以此来分辨不同方向不同颜色的汽车。这个模板上的车是红色的，这是因为 CIFAR-10 中训练集的车大多是红色的。

线性分类器对于不同颜色的车的分类能力是很弱的，但是后面可以看到神经网络是可以完成这一任务的。神经网络可以在它的隐藏层中实现中间神经元来探测不同种类的车（比如绿色车头向左，蓝色车头向前等）。而下一层的神经元通过计算不同的汽车探测器的权重和，将这些合并为一个更精确的汽车分类分值。

1. 图像空间的示意图。其中每个图像是一个点，有 3 个分类器。以红色的汽车分类器为例，红线表示空间中汽车分类分数为 0 的点的集合，红色的箭头表示分值上升的方向。所有红线右边的点的分数值均为正，且线性升高。红线左边的点分值为负，且线性降低。

从上面可以看到，W 的每一行都是一个分类类别的分类器。对于这些数字的几何解释是：如果改变其中一行的数字，会看见分类器在空间中对应的直线开始向着不同方向旋转。而偏差b，则允许分类器对应的直线平移。 需要注意的是，如果没有偏差，无论权重如何，分类分值始终为 0。这样所有分类器的线都不得不穿过原点。

summary:

图像数据预处理：在上面的例子中，所有图像都是使用的原始像素值（从 0 到 255）。在机器学习中，对于输入的特征做归一化（normalization）处理是常见的套路。而在图像分类的例子中，图像上的每个像素可以看做一个特征。在实践中，对每个特征减去平均值来 中心化 数据是非常重要的。在这些图片的例子中，该步骤意味着根据训练集中所有的图像计算出一个平均图像值，然后每个图像都减去这个平均值，这样图像的像素值就大约分布在 [-127, 127] 之间了。下一个常见步骤是，让所有数值分布的区间变为 [-1, 1]。零均值的中心化 是很重要的，等我们理解了梯度下降后再来详细解释。

损失函数 Loss function

在上一节定义了从图像像素值到所属类别的评分函数（score function），该函数的参数是权重矩阵 W。在函数中，数据(\(x_i, y_i\))是给定的，不能修改。但是我们可以调整权重矩阵这个参数，使得评分函数的结果与训练数据集中图像的真实类别一致，即评分函数在正确的分类的位置应当得到最高的评分（score）。

我们将使用 损失函数（Loss Function）（有时也叫 代价函数 Cost Function 或 目标函数 Objective function）来衡量我们对结果的不满意程度。直观地讲，当评分函数输出结果与真实结果之间差异越大，损失函数输出越大，反之越小。

• Loss for a single example is\(L_i(f_i(x_i, W),y_i)\)

• Loss for the dataset is average of per-example losses :\(L = \dfrac{1}{N}\sum L_i(f(x_i,W),y_i)\)

0-1 损失

这是一种最完美的损失函数，理论上可以满足我们的需要，找到最佳的优化目标，但是没办法在程序中实现.

只看分类的对与错，当标签与预测类别相等时，loss = 0，否则为 1

\[ L(f_i(x_i, W), y_i) = \begin{cases} 0 & if \ y_i = f_i(x_i, W)\\ 1 & if \ y_i != f_i(x_i, W) \end{cases} \]

交叉熵损失

熵表示热力学系统的无序程度，在信息学中可以表示信息的无序程度，在图像分类中，真实标签向量只有一个元素为 1，这种情况无序程度最低，这也是我们期望模型输出可以达到的程度。

\[ entropy = -\sum_{i = 0}^i p_ilogp_i \]

交叉熵损失可以衡量两个向量之间的差异程度，并且只关心正确分类的问题，不会去关心错误分类的概率，可以使得模型更专注于强化正确分类的概率

\(y_{ij}\)表示第\(i\)个样本属于第\(j\)类标签的概率（0 或 1），\(f(x_{ij})\)表示第\(i\)个样本被预测为第\(j\)类标签的概率

\[ l(f, y) = -\sum_i^n \sum_j^m y_{ij}logf(x_{ij}) \]

交叉熵损失函数实际上是在度量实际分类与预测分类之间的差异。当实际分类和预测分类差异增大时，交叉熵损失函数的值会增加，反之减少。

• 熵增（损失增大）：当预测的概率分布\(f(x_{ij})\)偏离真实分布\(y_{ij}\)时（即预测错误），损失函数值会增大。例如，如果\(y_{ij} = 1\)但\(f(x_{ij})\)非常接近 0，那么\(\log f(x_{ij})\)会趋向于负无穷大，从而导致损失函数值增大。
• 熵减（损失减小）：当预测的概率分布\(f(x_{ij}\)) 越接近真实分布\(y_{ij}\)时（即预测正确），损失函数值会减小。例如，如果\(y*{ij} = 1\)且\(f(x*{ij})\)越接近 1，那么\(\log f(x_{ij})\)也会接近 0，从而使得损失值减小。

KL 散度

KL 散度（Kullback-Leibler Divergence，也称为相对熵）是用来衡量两个概率分布之间差异的一种方法。在信息论中，KL 散度可以用来描述从一个分布预测另一个分布的代价。

假设有两个概率分布 P 和 Q，其中 P 是真实分布，Q 是预测分布。KL 散度定义为：

\[ D_{KL}(P \parallel Q) = \sum_i P(i) \log \frac{P(i)}{Q(i)} \]

或者在连续情况下：

\[ D_{KL}(P \parallel Q) = \int P(x) \log \frac{P(x)}{Q(x)} \, dx \]

KL 散度可以被理解为使用分布 Q 代替分布 P 时增加的“额外信息”或“信息损失”。换句话说，KL 散度量化了在使用 Q 来描述数据而不是 P 时所付出的代价。越大的 KL 散度表示 Q 越不接近 P，预测误差越大。

交叉熵和 KL 散度之间有密切的关系。交叉熵可以写成：

\[ H(P, Q) = H(P) + D_{KL}(P \parallel Q) \]

其中，H(P) 是分布 P 的熵，而 H(P, Q) 是 P 和 Q 之间的交叉熵。交叉熵等于真实分布的熵加上 KL 散度，因此最小化交叉熵损失函数也在最小化 KL 散度。

多类支持向量机损失 Multiclass Support Vector Machine Loss

介绍常用的多类支持向量机（SVM）损失函数。SVM 的目标是确保正确分类的得分比不正确分类的得分高出至少一个边界值\(\Delta\)。如果不满足这一条件，就会产生损失。

第 i 个数据中包含图像\(x_i\)的像素数据和代表正确类别的标签\(y_i\)。评分函数输入像素数据，然后通过公式\(f(x_i,W)\)来计算不同分类类别的分值。这里我们将分值简写为 s。比如，针对第 j 个类别的得分就是第 j 个元素：\(s_{j}=f(x_{i},W)_{j}\)。针对第 i 个数据的多类 SVM 的损失函数定义如下：

\[ L_i =\sum_{j\not = y_i}\max(0, s_j-s_{y_i}+\Delta) \]

举例：用一个例子演示公式是如何计算的。假设有 3 个分类，并且得到了分值\(s = [13,-7,11]\)。其中第一个类别是正确类别，即\(y_i=0\)。同时假设\(\Delta\)是 10（后面会详细介绍该超参数）。上面的公式是将所有不正确分类（\(j\not=y_i\)）加起来，所以我们得到两个部分：

\[ L_i =\max(0,-7-13+10)+\max(0,11-13+10) \]

可以看到第一个部分结果是 0，这是因为 [-7-13+10] 得到的是负数，经过\(\max(0,-)\)函数处理后得到 0。这一对类别分数和标签的损失值是 0，这是因为正确分类的得分 13 与错误分类的得分-7 的差为 20，高于边界值 10。而 SVM 只关心差距至少要大于 10，更大的差值还是算作损失值为 0。第二个部分计算 [11-13+10] 得到 8。虽然正确分类的得分比不正确分类的得分要高（13 > 11），但是比 10 的边界值还是小了，分差只有 2，这就是为什么损失值等于 8。简而言之，SVM 的损失函数想要正确分类类别$y_i$的分数比不正确类别分数高，而且至少要高$\Delta$。如果不满足这点，就开始计算损失值。

那么在这次的模型中，我们面对的是线性评分函数（\(f(x_i,W)=Wx_i\)），所以我们可以将损失函数的公式稍微改写一下：

\[ L_i =\sum_{j\not = y_i}\max(0, w^T_jx_i-w^T_{y_i}x_i+\Delta) \]

其中\(w_j\)是权重\(W\)的第 j 行，被变形为列向量。然而，一旦开始考虑更复杂的评分函数\(f\)公式，这样做就不是必须的了。

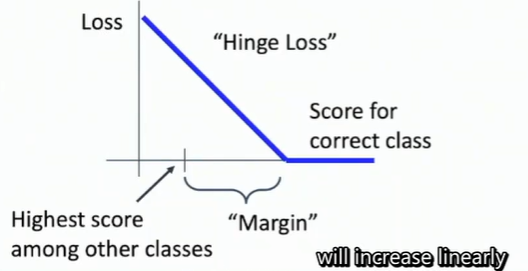
在结束这一小节前，还必须提一下的属于是关于 0 的阀值：\(\max(0,-)\)函数，它常被称为 折叶损失（hinge loss）。有时候会听到人们使用平方折叶损失 SVM（即 L2-SVM），它使用的是\(\max(0,-)^2\)，将更强烈（平方地而不是线性地）地惩罚过界的边界值。不使用平方是更标准的版本，但是在某些数据集中，平方折叶损失会工作得更好。可以通过 交叉验证 来决定到底使用哪个。

---

多类 SVM "想要" 正确类别的分类分数比其他不正确分类类别的分数要高，而且至少高出 delta 的边界值。如果其他分类分数进入了红色的区域，甚至更高，那么就开始计算损失。如果没有这些情况，损失值为 0。我们的目标是找到一些权重，它们既能够让训练集中的数据样例满足这些限制，也能让总的损失值尽可能地低。

正则化 Regularization

正则化（Regularization）是机器学习中常用的技术，用来防止模型过拟合并提高泛化能力。在多类 SVM 的背景下，正则化通过增加惩罚项来控制模型的复杂度，从而减少权重的模糊性和避免过度依赖某些特定的输入维度。

正则化（Regularization）动机： 上面损失函数有一个问题。假设有一个数据集和一个权重集 W 能够正确地分类每个数据（即所有的边界都满足，对于所有的 i 都有\(L_i=0\)）。问题在于这个 W 并不唯一：可能有很多相似的 W 都能正确地分类所有的数据。一个简单的例子：如果 W 能够正确分类所有数据，即对于每个数据，损失值都是 0。那么当\(\lambda >1\)时，任何数乘\(\lambda W\)都能使得损失值为 0，因为这个变化将所有分值的大小都均等地扩大了，所以它们之间的绝对差值也扩大了。 举个例子，如果一个正确分类的分值和举例它最近的错误分类的分值的差距是 15，对 W 乘以 2 将使得差距变成 30。

换句话说，我们希望能向某些特定的权重 W 添加一些偏好，对其他权重则不添加，以此来消除模糊性。这一点是能够实现的，方法是向损失函数增加一个 正则化惩罚（regularization penalty）\(R(W)\)]部分。

最常用的正则化惩罚是 L2 范式，L2 范式通过对所有参数进行逐元素的平方惩罚来抑制大数值的权重：\(R(W)=\sum_k\sum_lW^2_{k,l}\)

上面的表达式中，将\(W\)中所有元素平方后求和。注意正则化函数不是数据的函数，仅基于权重。包含正则化惩罚后，就能够给出完整的多类 SVM 损失函数了，它由两个部分组成：数据损失（data loss），即所有样例的的平均损失\(L_i\)，以及 正则化损失（regularization loss）。完整公式如下所示：

\[ L = \underbrace{ \frac{1}{N}\sum_i L_i}_{data loss}+\underbrace{\lambda R(W)}_{regularization loss} \]

将其展开完整公式是：

\[ L = \frac{1}{N}\sum_i\sum_{j\not = y_i} \left [ \max(0, f(x_i; W)_j-f(x_i; W)_{y_i}+\Delta )\right] + \lambda\sum_k\sum_l W_{k, l}^2 \]

其中，\(N\)是训练集的数据量。现在正则化惩罚添加到了损失函数里面，并用超参数\(\lambda\)来计算其权重。该超参数无法简单确定，需要通过交叉验证来获取。

正则化有许多重要作用：

• 控制模型复杂度：通过惩罚大权重，L2 正则化抑制模型的复杂性(prefe simple models)，鼓励权重值更小且更均匀地分布在各个维度上。

• 提升泛化能力：避免模型依赖于少数几个特征，从而减少过拟合现象。

• 最大边界性质：在 SVM 中，正则化促使模型寻找最大化分类边界的解，这增强了模型的稳定性和鲁棒性。

其中最好的性质就是对大数值权重进行惩罚，可以提升其泛化能力，因为这就意味着没有哪个维度能够独自对于整体分值有过大的影响。举个例子，假设输入向量\(x = [1,1,1,1]\)，两个权重向量\(w_1=[1,0,0,0]\)，\(w_2=[0.25,0.25,0.25,0.25]\)。那么\(w^T_1x=w^T_2x=1\)，两个权重向量都得到同样的内积，但是\(w_1\)的 L2 惩罚是 1.0，而\(w_2\)的 L2 惩罚是 0.25。因此，根据 L2 惩罚来看，\(w_2\)更好，因为它的正则化损失更小。

从直观上来看，这是因为\(w_2\)的权重值更小且更分散。既然 L2 惩罚倾向于更小更分散的权重向量，这就会鼓励分类器最终将所有维度上的特征都用起来，而不是强烈依赖其中少数几个维度。在后面的课程中可以看到，这一效果将会提升分类器的泛化能力，并避免 过拟合。

需要注意的是，和权重不同，偏差没有这样的效果，因为它们并不控制输入维度上的影响强度。因此通常只对权重\(W\)正则化，而不正则化偏差\(b\)。在实际操作中，可发现这一操作的影响可忽略不计。最后，因为正则化惩罚的存在，不可能在所有的例子中得到 0 的损失值，这是因为只有当\(W=0\)的特殊情况下，才能得到损失值为 0。

非向量化

代码片段展示了计算多类 SVM 损失的三种实现方式：非向量化（L_i）、部分向量化（L_i_vectorized）和完全向量化（L）。每个实现的目标是计算样本集上的多类 SVM 损失。

def L_i(x, y, W):
    delta = 1.0
    scores = W.dot(x)  # 计算所有类别的得分
    correct_class_score = scores[y]  # 获取正确类别的得分
    D = W.shape[0]  # 类别数量，例如在 CIFAR-10 中为 10
    loss_i = 0.0
    for j in xrange(D):  # 遍历所有类别
        if j == y:
            continue  # 跳过正确类别
        # 计算每个错误类别的损失，并累加
        loss_i += max(0, scores[j] - correct_class_score + delta)
    return loss_i

• W.dot(x)：计算所有类别的得分，这里 W 是权重矩阵，x 是样本向量。结果是一个大小为 [D, 1] 的向量，每个元素代表一个类别的得分。

• correct_class_score：提取正确类别的得分。

• for j in xrange(D)：遍历所有类别，计算错误类别的损失，忽略正确类别的损失。

• loss_i += max(0, scores[j] - correct_class_score + delta)：使用折叶损失（hinge loss），如果错误类别的得分高于正确类别的得分加上一个 delta（边界值），则产生损失。

双重循环：外层循环遍历所有样本，内层循环遍历所有类别。

低效：当样本量和类别数量较大时，计算速度慢。

部分向量化

def L_i_vectorized(x, y, W):
    delta = 1.0
    scores = W.dot(x)  # 计算所有类别的得分
    margins = np.maximum(0, scores - scores[y] + delta)  # 计算所有类别的边距
    margins[y] = 0  # 正确类别的边距设为 0，不计入损失
    loss_i = np.sum(margins)  # 计算总损失
    return loss_i

• margins = np.maximum(0, scores - scores[y] + delta)：一次性计算所有类别的边距，并对每个类别应用折叶损失。
• margins[y] = 0：将正确类别的边距设置为 0，因为它不应该产生损失。
• loss_i = np.sum(margins)：将所有错误类别的损失加总。

• 效率提高：利用 NumPy 的矢量化操作，避免了显式的内部循环。

• 比非向量化高效：减少了内部循环。

完全向量化

def L(X, y, W):
    """
    全向量化实现的多类 SVM 损失函数。
    - X 保存所有训练样本的列向量（例如，在 CIFAR-10 数据集中，X 的形状为 3073 x 50,000）
    - y 是一个一维整数数组，指定正确类别的索引（例如，长度为 50,000 的数组）
    - W 是权重矩阵（例如，在 CIFAR-10 数据集中，W 的形状为 10 x 3073）
    """

    delta = 1.0  # 边界超参数
    num_train = X.shape[1]  # 训练样本的数量

    # 第一步：计算所有类别的得分
    scores = W.dot(X)  # 计算得分矩阵，形状为 [类别数量, 训练样本数量]

    # 第二步：从得分矩阵中提取正确类别的得分
    correct_class_scores = scores[y, np.arange(num_train)]  # 正确类别的得分，形状为 [1, 训练样本数量]

    # 第三步：计算所有类别的边距
    margins = np.maximum(0, scores - correct_class_scores + delta)  # 计算边距矩阵，形状为 [类别数量, 训练样本数量]

    # 第四步：不考虑正确类别的损失（将其边距设为 0）
    margins[y, np.arange(num_train)] = 0  # 对正确类别的边距设为 0

    # 第五步：计算所有样本的平均总损失
    loss = np.sum(margins) / num_train  # 计算总损失

    # 第六步：将正则化项添加到损失中
    regularization_strength = 0.5  # 正则化强度的超参数，可以根据需要调整
    loss += regularization_strength * np.sum(W * W)  # 添加正则化损失

    return loss  # 返回最终的损失值

• scores 矩阵的形状为 [num_classes, num_train]，即每一列对应一个样本，每一行对应一个类别的得分。

• correct_class_scores 提取出每个样本的正确类别的得分，形状为 [1, num_train]。

y 是正确类别的索引数组，通过 scores[y, np.arange(num_train)] 可以直接提取出对应列中的正确类别得分。

• margins 矩阵的形状与 scores 相同，为 [num_classes, num_train]。

对每个样本，计算它的所有类别的边距值，并通过 np.maximum 将负的边距值设为 0。

• 将 margins 中正确类别的边距值设为 0，因为我们不需要考虑它们的损失。

• 对所有样本和类别的边距值求和，然后除以样本总数，得到平均损失。

• 将正则化损失加到总损失中。正则化项是权重矩阵的 L2 范数的平方。

完全向量化实现 (L)：对所有样本和类别一次性完成计算，效率最高，适合处理大规模数据集。

最高效：使用 NumPy 的广播机制和矢量化操作，完全消除了显式的循环。

实际考虑

设置 Delta：你可能注意到上面的内容对超参数\(Delta\)及其设置是一笔带过，那么它应该被设置成什么值？需要通过交叉验证来求得吗？现在看来，该超参数在绝大多数情况下设为\(Delta=1.0\)都是安全的。超参数\(\Delta\)和\(\lambda\)看起来是两个不同的超参数，但实际上他们一起控制同一个权衡：即损失函数中的数据损失和正则化损失之间的权衡。 理解这一点的关键是要知道，权重$W$的大小对于分类分值有直接影响（当然对他们的差异也有直接影响）：当我们将\(W\)中值缩小，分类分值之间的差异也变小，反之亦然。因此，不同分类分值之间的边界的具体值（比如\(\Delta=1\)或\(\Delta=100\)）从某些角度来看是没意义的，因为权重自己就可以控制差异变大和缩小。也就是说 ，真正的权衡是我们允许权重能够变大到何种程度（通过正则化强度$\lambda$来控制）。

与二元支持向量机（ Binary Support Vector Machine ）的关系：在学习本课程前，你可能对于二元支持向量机有些经验，它对于第 i 个数据的损失计算公式是：

\[L_i=C\max(0,1-y_iw^Tx_i)+R(W)\]

其中，\(C\)是一个超参数，并且\(y_i\in{\left\{-1,1\right\}}\)。可以认为本章节介绍的 SVM 公式包含了上述公式，上述公式是多类支持向量机公式只有两个分类类别的特例。也就是说，如果我们要分类的类别只有两个，那么公式就化为二元 SVM 公式。这个公式中的\(C\)和多类 SVM 公式中的\(\lambda\)都控制着同样的权衡，而且它们之间的关系是\(C\propto\frac{1}{\lambda}\)

Softmax 分类器

1. SVM（支持向量机）

• 损失函数: SVM 使用的是 Hinge Loss（折叶损失）。
• 输出: SVM 的输出是每个类别的原始分数，这些分数并不能直接解释为概率。
• 分类决策: 通过最大化类别间的边界来进行分类，即使得正确分类的分数与其他所有错误分类的分数之间有一个预定的间隔（delta）。
• 正则化: 通常通过在损失函数中添加 L2 正则化项来控制权重的大小，防止过拟合。

2. Softmax 分类器

• 损失函数: Softmax 分类器使用的是 Cross-Entropy Loss（交叉熵损失），该损失函数最小化的是预测概率分布与真实分布之间的差异。
• 输出: Softmax 分类器的输出是一个概率分布，表示每个类别的概率，并且这些概率的总和为 1。
• 分类决策: 通过最大化正确类别的概率来进行分类，确保模型对每个样本预测的正确类别概率尽可能高。
• 概率解释: Softmax 分类器的输出是直观的概率值，便于理解和解释。

SVM 是最常用的两个分类器之一，而另一个就是 Softmax 分类器， 它的损失函数与 SVM 的损失函数不同。对于学习过二元逻辑回归分类器的读者来说，Softmax 分类器就可以理解为逻辑回归分类器面对多个分类的一般化归纳。SVM 将输出\(f(x_i, W)\)作为每个分类的评分（因为无定标，所以难以直接解释）。

在 Softmax 分类器中，函数映射\(f(x_i; W)= Wx_i\)保持不变，其输出是线性分类器预测的原始分数，但将这些评分值视为每个分类的未归一化的对数概率（或者叫做非标准化的对数概率），进行指数计算之后，所有的分数转化为正数，并且将折叶损失（hinge loss）替换为 交叉熵损失（cross-entropy loss）。

\[ entropy = -\sum_{i = 0}^i p_ilogp_i \\ l(f, y) = -\sum_i^n \sum_j^m y_{ij}logf(x_{ij}) \]

Softmax 分类器使用 交叉熵损失函数 来衡量模型输出的概率分布与实际标签的差距。对于一个输入样本 xix_ixi 及其对应的真实标签 yiy_iyi，交叉熵损失函数可以写作：

\(Li=−log⁡P(y_i∣x_i)\)其中\(P(y_i∣x_i)\)是模型对样本\(x_i\)的正确类别\(y_i\)预测的概率。

公式如下：\(Li =-log(\dfrac{e^{f_{y_i}}}{\sum_je^{f_j}})\)或等价的\(L_i =-f_{y_i}+log(\sum_je^{f_j})\)

在上式中，使用\(f_j\)来表示分类评分向量\(f\)中的第\(j\)个元素(\(f_j = W_j \cdot x_i\))。和之前一样，整个数据集的损失值是数据集中所有样本数据的损失值\(L_i\)的均值与正则化损失\(R(W)\)之和。其中函数\(f_j(z)= \dfrac{e^{z_j}}{\sum_ke^{z_k}}\)被称作 softmax 函数：其输入值是一个向量，向量中元素为任意实数的评分值\(z\)中的），函数对其进行压缩，输出一个向量，其中每个元素值在 0 到 1 之间，且所有元素之和为 1。

因为原始的线性分类器输出的是原始分数，可以看做是非标准化/未归一化的对数概率，然后取指数，得到非标准化/未归一化概率，然后进行归一化，就可以得到所有类的离散概率分布

信息理论视角：在 "真实" 分布\(p\)和估计分布\(q\)之间的交叉熵定义如下：\(H(p, q)=-\sum_xp(x) logq(x)\)

-\(p(x)\)是真实分布（通常是独热编码，即在正确类别位置上为 1，其他位置为 0）。

-\(q(x)\)是模型的预测分布（Softmax 输出的归一化概率）。

因此，Softmax 分类器所做的就是 最小化 在估计分类概率（ 就是上面的\(e^{f_{y_i}}/\sum_{j}e^{f_j}\)）和 "真实" 分布之间的 交叉熵，在这个解释中，"真实" 分布就是所有概率密度都分布在正确的类别上（比如：\(p = [0, \cdots,1,\cdots,0]\)中在\(y_i\)的位置就有一个单独的 1）。还有，既然交叉熵可以写成熵和相对熵（Kullback-Leibler divergence）\(H(p, q)= H(p)+D_{KL}(p||q)\)，并且 delta 函数\(p\)的熵是 0，那么就能等价的看做是对两个分布之间的相对熵做最小化操作。换句话说，交叉熵损失函数 "想要" 预测分布的所有_概率密度_都在正确分类上。

当然我们可以这样子理解，W 表示权重，x 表示输入，z 表示输出，当三者都为向量的时候，可以理解为实际上优化预测概率就是在优化向量夹角

如图所示，如果两个类之间的夹角越大，则越容易进行区分，如果类所占区域的夹角很小，那么就说明类内更加紧凑，类间更容易分离，那么分类器学习起来更容易

类内紧凑性与类间分离:

当类别之间的夹角很小时，说明不同类别的特征之间的相似性较高，这会增加分类的难度。但如果类内的数据分布非常紧凑，类间的分离仍然较为明显，则分类器也能找到有效的决策边界。

• 类内紧凑性：指的是相同类别的样本在特征空间中分布得非常集中。类内越紧凑，分类器越容易捕捉到类别的特征中心，提升分类性能。
• 类间分离：如果类间的距离较大，即使夹角较小，分类器仍然能找到较好的边界来区分不同类别。

概率论解释：先看下面的公式：

\[ P(y_i|x_i, W)= \dfrac{e^{f_{y_i}}}{\sum_je^{f_j}} \]

可以解释为是给定图像数据\(x_i\)，以\(W\)为参数，分配给正确分类标签\(y_i\)的归一化概率。用\(W \cdot x_i\)得到的结果做指数函数的幂就得到了没有归一化的概率，而除法操作则对数据进行了归一化处理，使得这些概率的和为 1。从概率论的角度来理解，我们就是在最小化正确分类的负对数概率，这可以看做是在进行最大似然估计（MLE）。该解释的另一个好处是，损失函数中的正则化部分\(R(W)\)可以被看做是权重矩阵\(W\)的高斯先验，这里进行的是最大后验估计（MAP）而不是最大似然估计。

实操事项：数值稳定。 编程实现 softmax 函数计算的时候，中间项\(e^{f_{y_i}}\)和\(\sum_j e^{f_j}\)因为存在指数函数，所以数值可能非常大。除以大数值可能导致数值计算的不稳定，所以学会使用归一化技巧非常重要。如果在分式的分子和分母都乘以一个常数\(C\)，并把它变换到求和之中，就能得到一个从数学上等价的公式：

\[ \dfrac{e^{f_{y_i}}}{\sum_je^{f_j}}= \dfrac{Ce^{f_{y_i}}}{C\sum_je^{f_j}}=\dfrac{e^{f_{y_i}+logC}}{\sum_je^{f_j+logC}} \]

\(C\)的值可自由选择，不会影响计算结果，通过使用这个技巧可以提高计算中的数值稳定性。通常将\(C\)设为\(logC =-maxf_j\)。该技巧简单地说，就是应该将向量\(f\)中的数值进行平移，使得最大值为 0。代码实现如下：

    f = np.array([123, 456, 789]) # 例子中有3个分类，每个评分的数值都很大
    p = np.exp(f) / np.sum(np.exp(f)) # 不妙：数值问题，可能导致数值爆炸

    # 那么将f中的值平移到最大值为0：
    f -= np.max(f) # f becomes [-666, -333, 0]
    p = np.exp(f) / np.sum(np.exp(f)) # 现在OK了，将给出正确结果

SVM 和 Softmax 的比较

下图有助于区分这 Softmax 和 SVM 这两种分类器：

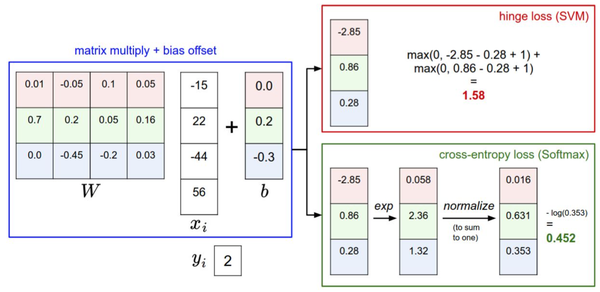
针对一个数据点，SVM 和 Softmax 分类器的不同处理方式的例子。两个分类器都计算了同样的分值向量 f（本节中是通过矩阵乘来实现）。不同之处在于对 f 中分值的解释：SVM 分类器将它们看做是分类评分，它的损失函数鼓励正确的分类（本例中是蓝色的类别 2）的分值比其他分类的分值高出至少一个边界值。Softmax 分类器将这些数值看做是每个分类没有归一化的 对数概率，鼓励正确分类的归一化的对数概率变高，其余的变低。 SVM 的最终的损失值是 1.58，Softmax 的最终的损失值是 0.452，但要注意这两个数值没有可比性。只在给定同样数据，在同样的分类器的损失值计算中，它们才有意义。

Softmax 分类器为每个分类提供了 "可能性"：SVM 的计算是无标定的，而且难以针对所有分类的评分值给出直观解释。Softmax 分类器则不同，它允许我们计算出对于所有分类标签的可能性。举个例子，针对给出的图像，SVM 分类器可能给你的是一个 [12.5, 0.6, -23.0] 对应分类 "猫"，"狗"，"船"。而 softmax 分类器可以计算出这三个标签的 "可能性" 是 [0.9, 0.09, 0.01]，这就让你能看出对于不同分类准确性的把握。

为什么我们要在 "可能性" 上面打引号呢？这是因为可能性分布的集中或离散程度是由正则化参数 λ 直接决定的，λ 是你能直接控制的一个输入参数。举个例子，假设 3 个分类的原始分数是 [1, -2, 0]，那么 softmax 函数就会计算：

\[ [1,-2,0]\rightarrow [e^1, e^{-2}, e^0] = [2.71,0.14,1]\rightarrow [0.7,0.04,0.26] \]

现在，如果正则化参数 λ 更大，那么权重 W 就会被惩罚的更多，然后他的权重数值就会更小。这样算出来的分数也会更小，假设小了一半 [0.5, -1, 0]，那么 softmax 函数的计算就是：

\[ [0.5,-1,0]\rightarrow [e^{0.5}, e^{-1}, e^0] = [1.65,0.73,1]\rightarrow [0.55,0.12,0.33] \]

随着正则化参数 λ 不断增强，权重数值会越来越小，最后输出的概率会接近于均匀分布。

SVM 的局部目标化：

• SVM 分类器主要关注正确类别与其他类别之间的 相对差异。只要正确类别的分数高于不正确类别的分数，并且超过一定的边界（即 Δ），SVM 就会认为损失为 0，不再进一步优化。
• 例如，对于 [10, -2, 3] 的评分，其中第一个分类是正确的，SVM 认为分数已经满足了边界条件（假设 Δ = 1），因此不会再优化该样本的分类结果。而且，无论分数是 [10, -100, -100] 还是 [10, 9, 9]，只要满足了边界条件，SVM 的损失值都是 0。

Softmax 的全局优化：

• Softmax 分类器则不同，它对每一个分类分数都进行考虑，并且 始终试图最大化正确类别的概率。Softmax 不会因为分数满足某个条件而停止优化，它会不断尝试让正确类别的分数更高、不正确类别的分数更低。
• 在 [10, 9, 9] 和 [10, -100, -100] 的情况下，Softmax 会给出不同的损失值：前者损失值较高，因为不正确类别的分数较高；而后者损失值较低，因为不正确类别的分数已经非常低。

SVM 的特性和局限

• 特性：SVM 专注于正确类别和不正确类别的差距是否超过一定的阈值。当这个阈值被满足时，SVM 不再关注具体的分数细节。因此，它在面对不需要过度区分的简单分类任务时可以表现得很好。例如，在汽车分类任务中，SVM 可能会将更多的注意力放在区分相似的汽车类型上，而不会在明显不同的物体（如青蛙）上花费太多精力。
• 局限：这种“局部目标化”的方法在某些情况下可能不是最优的，因为它忽略了进一步优化的机会。例如，如果两个不正确类别的分数接近正确类别，SVM 可能会认为损失已经足够小，而不再进一步优化，这可能导致分类器在面对复杂任务时表现不如 Softmax。

Softmax 的优点和缺点

• 优点：Softmax 分类器总是尝试最小化分类损失，即使对于那些已经满足某些条件的样本，它也会继续优化。这使得 Softmax 能够在复杂的分类任务中提供更精细的区分能力。
• 缺点：由于 Softmax 分类器总是不断优化，它可能在一些简单的任务中浪费计算资源。例如，在某些情况下，Softmax 可能会过度关注一些无关紧要的细节（如如何进一步降低一个已经很低的错误分类分数），而这些并不会显著提高分类性能。