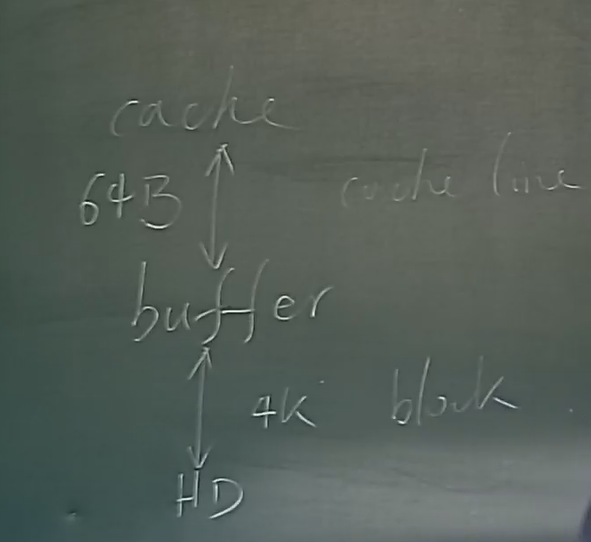10. Indexing

约 4731 个字 预计阅读时间 24 分钟

Abstract

• Basic Concepts
• Ordered Indices
• B+-Tree Index
• B+-Tree File Organization
• B-Tree Index Files
• Indices on Multiple Keys
• Indexing on Flash
• Indexing in Main Memory
• Write Optimized Indices
• Log Structured Merge (LSM) Tree
• Buffer Tree
• Bitmap Indices

10.1 Basic Concepts

Indexing mechanisms used to speed up access to desired data.

Search Key - attribute to set of attributes used to look up records in a file.

搜索键 - 用于查找文件中的记录的一组属性的属性。

An index file consists of records (called index entries) of the form.

索引文件由表单的记录（称为索引条目）组成。

Two basic kinds of indices:

• Ordered indices: search keys are stored in sorted order

• Hash indices: search keys are distributed uniformly across “buckets” using a “hash function”.

10.1.1 Index Evaluation Metrics

评估指标

• Access types supported efficiently
  • Point query: records with a specified value in the attribute. 点查询：属性中具有指定值的记录
  • Range query: records with an attribute value falling in a specified range of values. 范围查询：属性值落在指定值范围内的记录。
• Access time
• Insertion time
• Deletion time
• Space overhead

10.2 Ordered Indices

• Primary index（主索引）: in a sequentially ordered file, the index whose search key specifies the sequential order of the file.

  主索引：在按顺序排序的文件中，其搜索键指定文件顺序的索引。也就是说文件恰好按照search key 进行排序

  • Also called clustering index（聚集索引）

  • The search key of a primary index is usually but not necessarily the primary key.

  search key通常是主键，但是不一定是主键，因为primary key可能由多个属性组合，但是search只能是一种

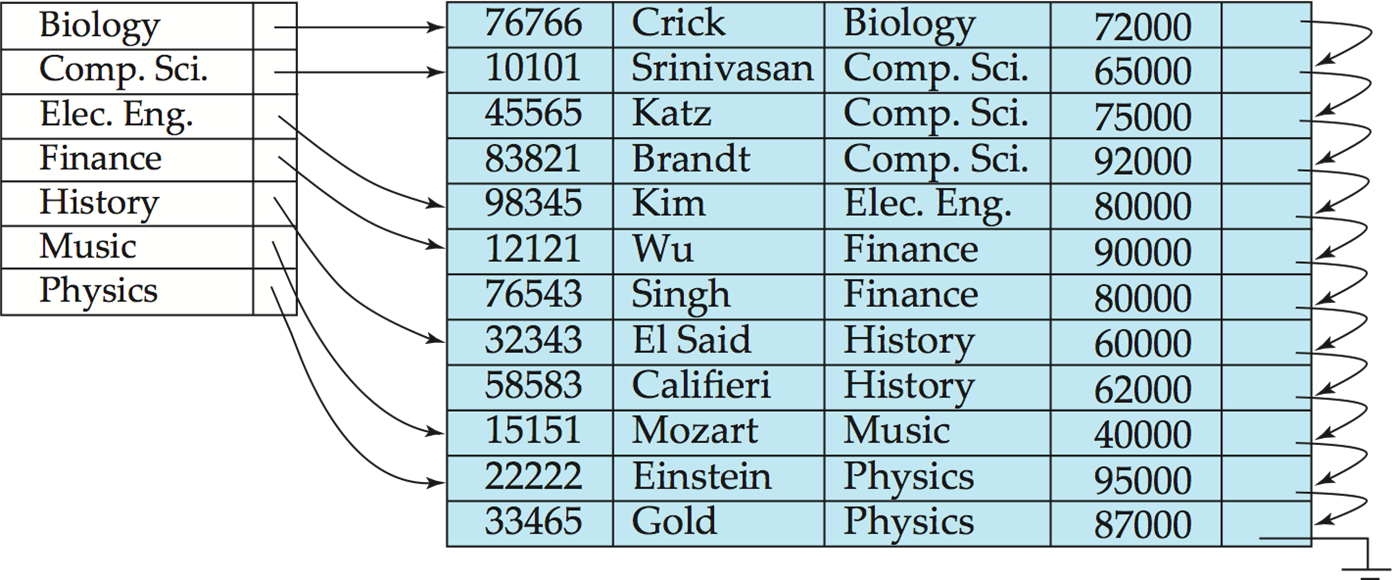
• Secondary index（辅助索引）: an index whose search key specifies an order different from the sequential order of the file. Also called non-clustering index.

  辅助索引：搜索键指定的顺序与文件的顺序不同的索引（例如：学生的学号搜索和id不一致）

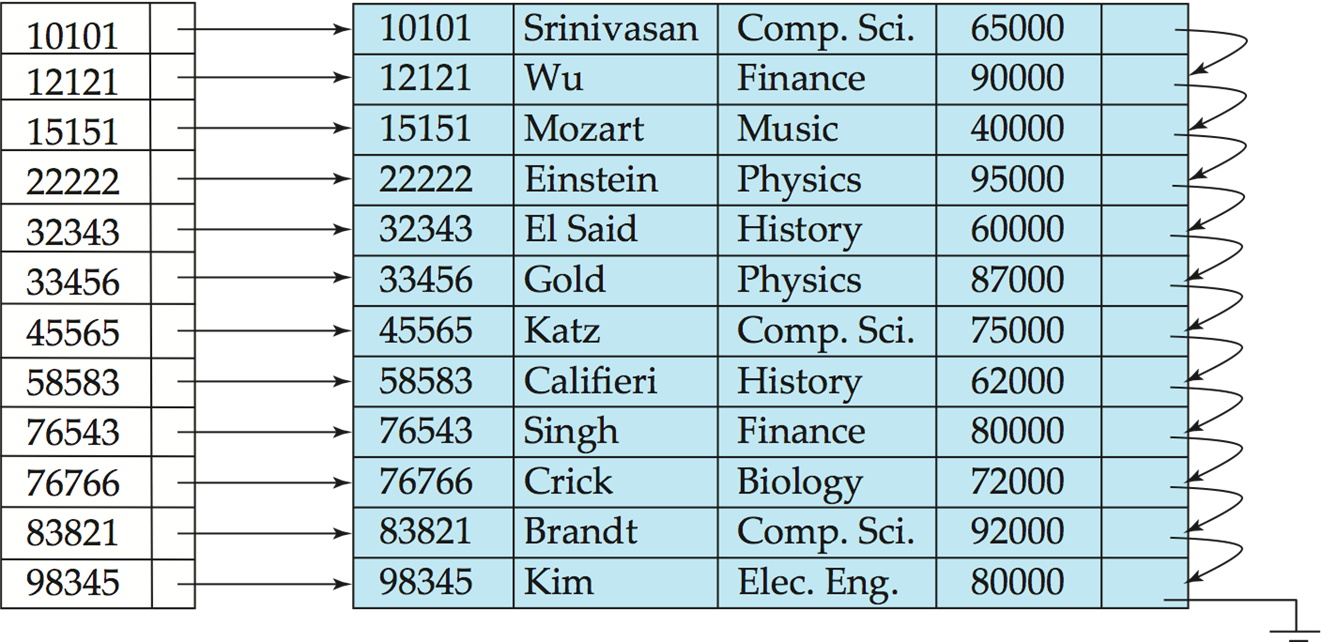
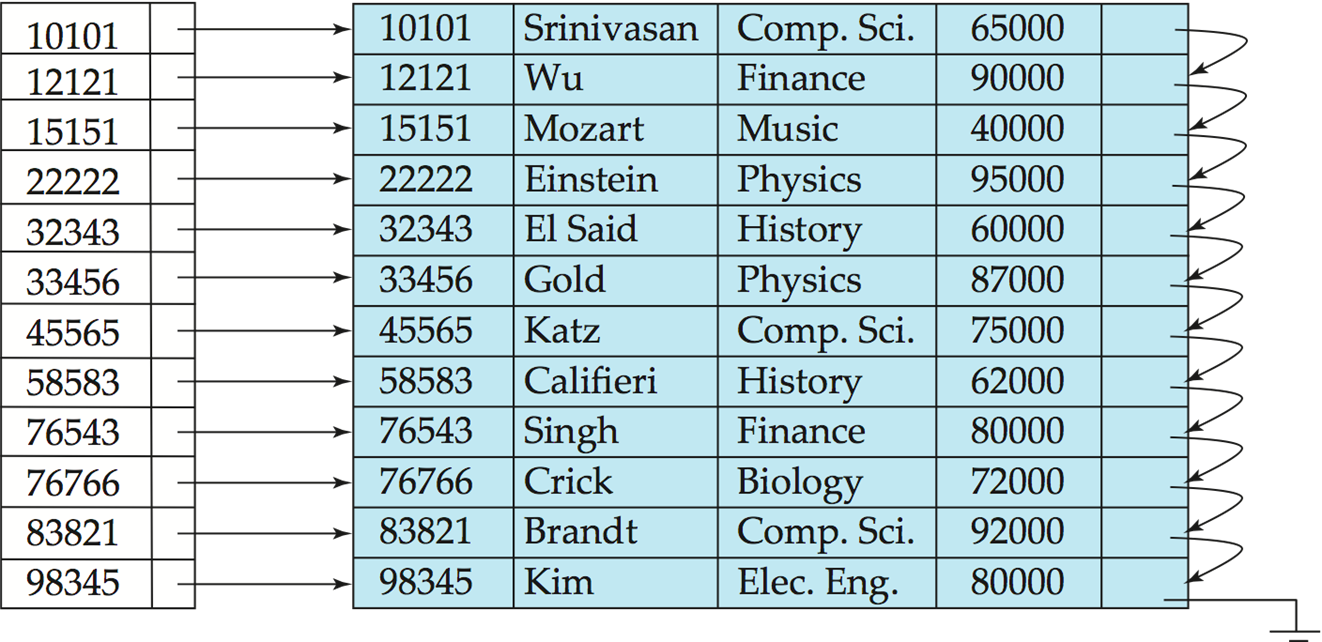
primary index on ID attribute of instructor

主索引和数据内的顺序是一样的。点查和范围查都是比较高效的。

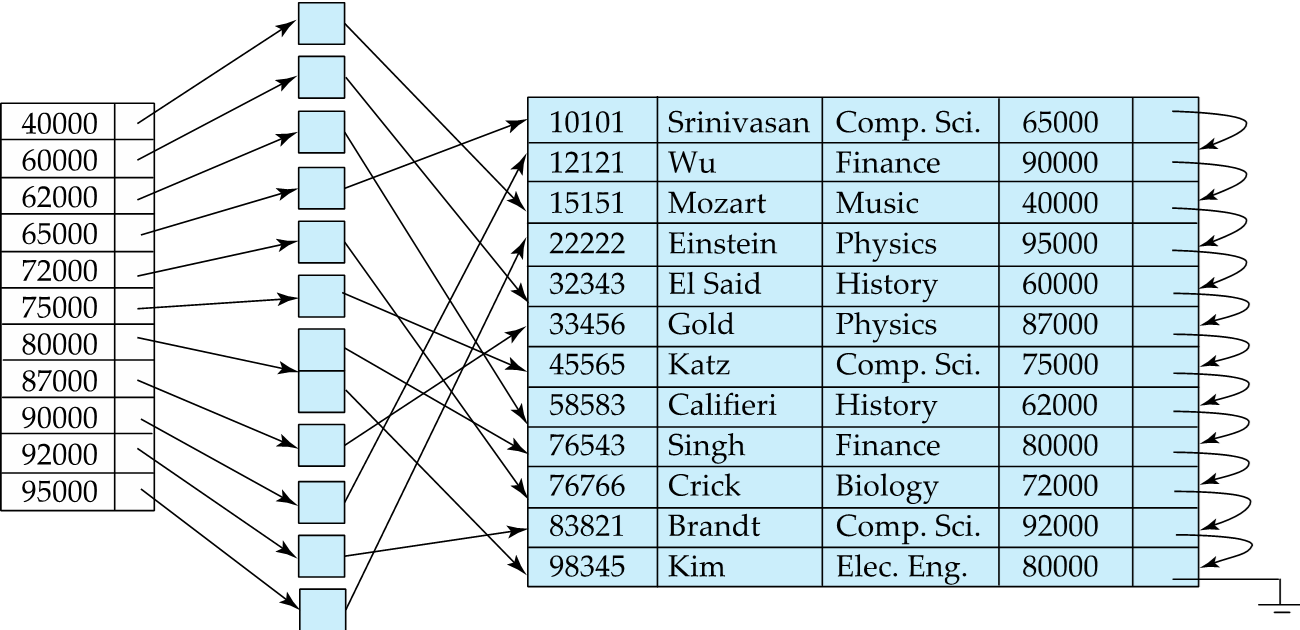
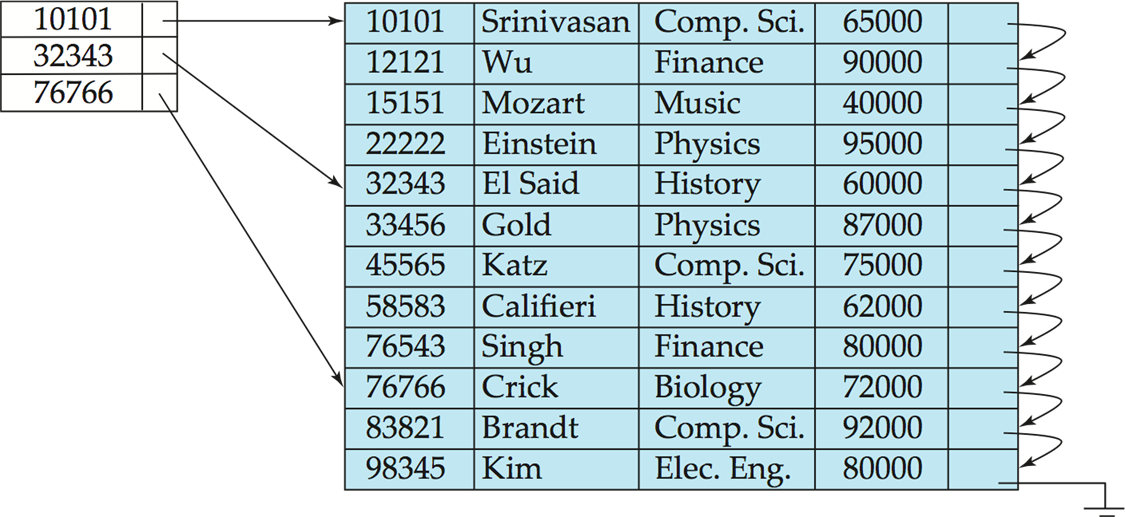
Secondary index on salary attribute of instructor

如果 key 不是一个主键，那可能会对应多个记录。

工资作为辅助索引，点搜索，需要先收集所有指定工资的老师的地址，再用一个头指针联系在一起。value -> 头结点（多个） -> 结果

Primary index 是很宝贵的，只能有一个，其他都是辅助索引。

• Dense index(稠密索引) — Index record appears for every search-key value in the file.

  每一个数据文件中的索引值，都要出现在索引文件里面。

根据搜索结果，每一个搜索键值都有一个索引

• Sparse Index（稀疏索引）: contains index records for only some search-key values.

  稀疏索引（稀疏索引）：仅包含某些搜索键值的索引记录。

  

  • Less space and less maintenance overhead for insertions and deletions.

    更少的空间和更少的插入和删除维护开销。

  • Generally slower than dense index for locating records.

    用于查找记录，通常比密集索引慢，

Good tradeoff: sparse index with an index entry for every block in file, corresponding to least search-key value in the block.

良好的权衡：稀疏索引，文件中每个块都有一个索引条目，对应于块中的最小搜索键值。

• Multilevel Index 多级索引

如果主索引不适合放在内存（索引过大），此时访问会变得十分高昂

解决方案：将保存在磁盘上的主索引看作是一个顺序文件，在主索引上进一步构造稀疏索引

• 外部索引——主索引的稀疏索引
• 内部索引——primary index

如果外部索引依然过大，可以针对外部索引进一步创建索引。从记录文件中插入或者删除时，必须更新所有级别的索引。

10.3 B+-Tree Index

• All paths from root to leaf are of the same length

  从根到叶的所有路径都具有相同的长度

• Inner node(not a root or a leaf): between \(\lceil n/2\rceil\) and \(n\) children.

  内部节点（不是根或叶）：\(\lceil n/2\rceil\) 到 \(n\) 个孩子

• Leaf node: between \(\lfloor n/2\rfloor\) and \(n–1\) values

• Special cases:

  • If the root is not a leaf: at least 2 children.
  • If the root is a leaf : between 0 and (n–1)values.

一般一个节点就是一个数据块的大小, 4K.

B+ 树的叉是非常多的，相应的高度就很低。

eg: 假设存放的数据是学号占10 bytes，指针占4 bytes，那么分叉数(max)= （4096 / （10+4））+1 = 293. 分叉数(min) = \(\lceil n/2\rceil\) = 147

关于inner node结点的结构

你会发现指针的数量是value数量+1，说明分叉数(孩子数)是serach key value数量+1

关于叶结点的结构

• 由于B+树的叶结点只能够\(n-1\)个value，所以对于$ i = 1， 2， . . .， n–1\(，指针\) Pi$ 指向搜索键值为 \(Ki\) 的文件记录
• 多出来的指针\(P_n\)指向下一个叶子结点，也就是将所有的叶子结点连接在一起

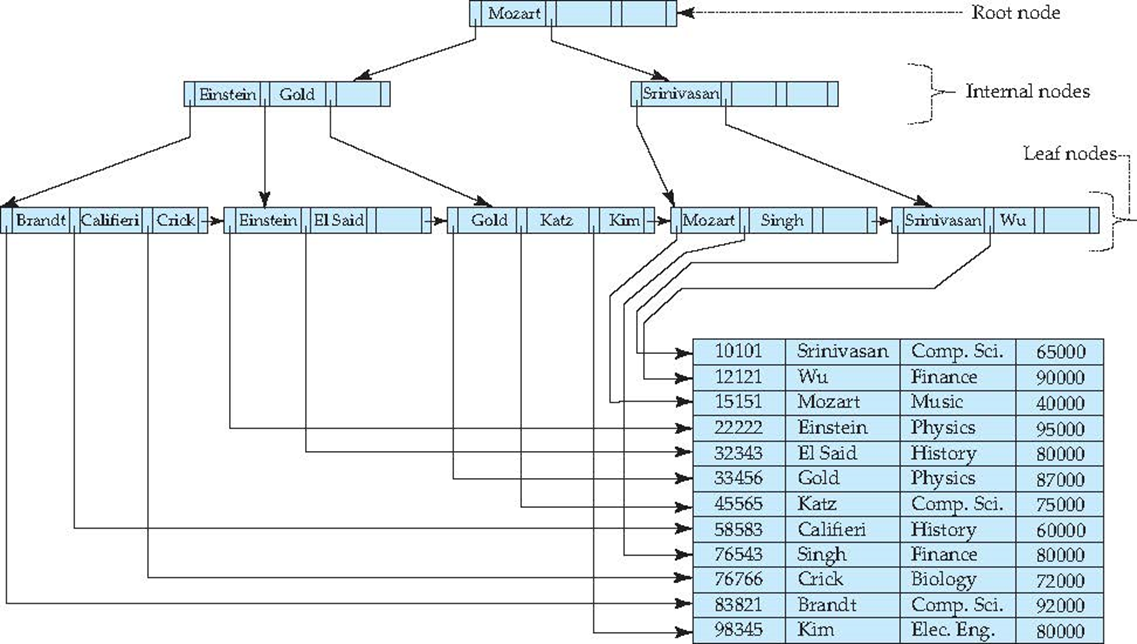
*Example of B+-tree*

• B+-tree for instructor file (n = 6) 内部结点指针最大个数（分叉数）

• Leaf nodes must have between 3 and 5 values

  between \(\lceil (n–1)/2\rceil\) and \(n–1\) values

• Non-leaf nodes other than root must have between 3 and 6 children

  between \(\lceil n/2\rceil\) or \(\lfloor (n+1)/2 \rfloor\)and \(n\) children.

  相应的value的数量为between\(\lceil n/2\rceil - 1\) and \(n–1\)

• Root must have at least 2 children.

10.3.1 Observations about B+-trees

如果有很多文件一次性建立 B+ 树，我们可以从叶子节点开始建立。

• Level below root has at least \(2 \times \lceil n/2\rceil\) 指针

  每一个inner node 最少具有\(\lfloor (n+1)/2 \rfloor\)个指针

  根结点至少有两个孩子

• Next level has at least \(2 \times \lceil n/2\rceil \times \lceil n/2\rceil\)指针s

  如果有 K 个索引项（K个根结点），则树高度不会超过 \(\lceil \log_{\lceil n/2 \rceil}(K/2)\rceil + 1\). 高度最小为 \(\log_n(K)\)

10.3.2 Find & Insert & Delete

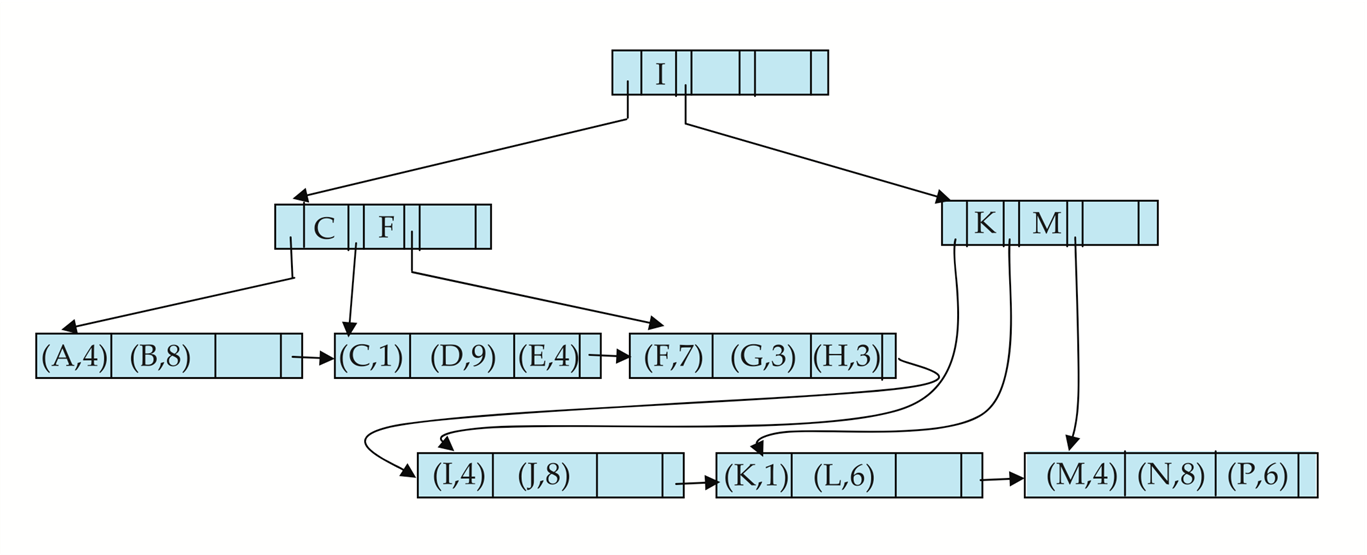
Example “Query on B+ Tree”

对于range query，先找到下界和上界，再利用leaf是利用指针连接在一起的，所以能获得结果

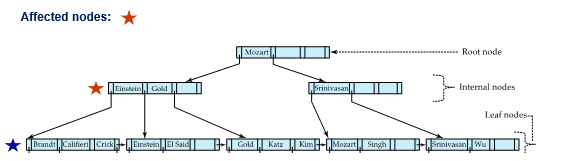
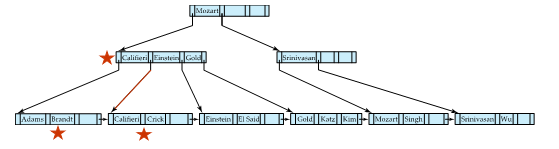
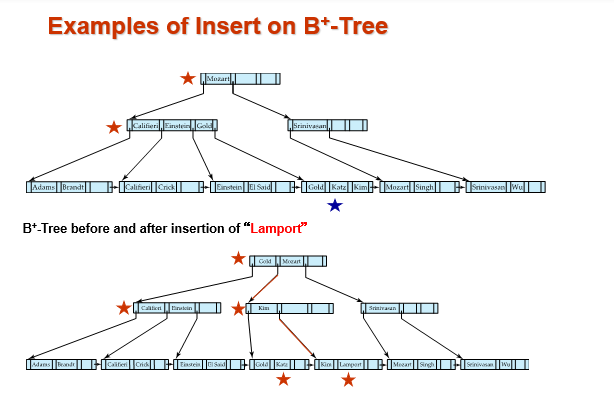
Example "Examples of Insert on B+-Tree"

B+-Tree before and after insertion of “Adams ”

inner node 的 split

注意内点的 split 和叶子的不一样。要把中间的节点 move 上去。

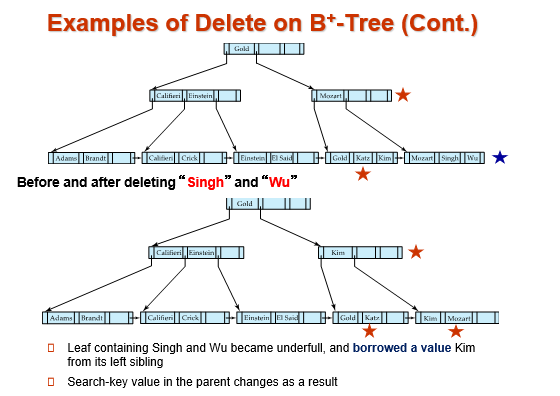
Example "Examples of Delete on B+-Tree"

当一个blcok中的记录被删除时，判断此时这个叶结点中value的数量是否大于等于\(\lfloor n/2 \rfloor\)。如果小于了，就要寻求与兄弟结点合并。

• 如果可以与兄弟结点合并，就要在合并之后，检查父亲结点的指针数目是否大于等于\(\lfloor (n+1)/2 \rfloor\),依次类推
• 如果不能合并，兄弟节点的value已经满了。那么就从兄弟结点中借一条记录，补充到当前结点

10.3.3 B+- tree : height and size estimation

假设一个block的大小是4K，每一个person的大小是68，因此一个block中的记录数量是60个。

为了记录1000000个person，我们需要16667个block。

B+树的叶子结点不再放入记录指针，而是放入记录本身

下面计算B+树的n。由于B+树的一个块是4096大小，包含n个指针（大小为4），与n-1个关键字大小（为pid，大小为18），因此计算公式为：\(（4096-4）/(18+4) + 1 = 187\)。

对于内部结点，其孩子指针最多有n = 187个，其孩子指针最少有\(\lceil n/2 \rceil = 94\)个，对于叶子结点，value最多有\(n-1 = 186\)个，最少有\(94 -1 = 93\)个

两层太少，四层太多，可以判断出，表示1000000个person，需要这样的B+树恰好是三层。

求出用三层的n为187的B+树来表示1000000个person，所需结点数目的最小值和最大值

• 最大值：对于叶结点，让叶结点保留最少的value，也就是93，此时所需的叶结点数量最多,需要\(1000000 / 93 = 10752.69\),注意这里需要向下取整，否则会有叶结点的value小于93。第二层的计算和根结点的计算都是用最少的指针数94，需要\(\lfloor 10752/94 \rfloor = 114\),最后还需要一个根结点。

  最终需要\(10752 + 114 + 1 = 10867\)个结点

• 对于叶节点，最多有186个值，因此叶节点最少个数可以用\(1000000/186\)，得到5736.344，注意这里要进行上取整，否则将至少有一个叶结点包含的值大于186个。其余第二层与根节点的计算以此类推，由于第二层的孩子个数最多为187个，因此第二层将5377除以187，并且向上取整。

  最终需要\(5377 + 29 + 1 = 5407\)个结点

10.4 B+-Tree File Organization

File Organization: heap堆结构，sequential顺序结构，hash结构，B+树结构

文件组织 B+-Tree File Organization:

• Leaf nodes in a B+-tree file organization store records, instead of pointers

  叶子节点不再放索引项，放记录本身。

• Helps keep data records clustered even when there are insertions/deletions/updates

我们可以改变半满的要求以提高空间利用率。

10.4.1 Other Issues in Indexing

• Record relocation and secondary indices

  记录搬迁和辅助索引

  If a record moves, all secondary indices that store record pointers have to be updated

  如果记录移动，则必须更新存储记录指针的所有辅助索引

  Node splits in B+-tree file organizations become very expensive

  Solution: use primary-index search key instead of record pointer in secondary index

  解决方案：在辅助索引中使用主索引搜索键而不是记录指针

  例如：利用学生的名字找到primary key（辅助索引），再利用primary key对应物理地址（主索引），一旦地址改变，只需要修改主索引中的primary key即可

  好处是：地址改变时只需要修改局部，坏处是：查找时需要先找到primary key，再通过primary key找到对应的地址

• Variable length strings as keys 变长字符串作为key

  Variable fanout 使用空间利用率（space utilization）作为拆分的标准，而不是指针数

• Prefix compression 前缀压缩

  Key values at internal nodes can be prefixes of full key

  内部节点的键值可以是完整键的前缀

  Keep enough characters to distinguish entries in the subtrees separated by the key value

  保留足够的字符来区分子树中由键值分隔的条目

  Keys in leaf node can be compressed by sharing common prefixes

  叶节点中的键可以通过共享公共前缀来压缩

10.5 Bulk Loading and Bottom-Up Build

10.5.1 Bottom-Up Build

Inserting entries one-at-a-time into a B+-tree requires \(\geq 1\) IO per entry

给定一大批的数据，需要建立B+树索引，相当于要一次性插入很多索引项

• Efficient alternative 1: Insert in sorted order

  先排序再插入，局部性较好，减少 I/O.

  缺点：大多数叶节点是半满的，B+树效率较低。

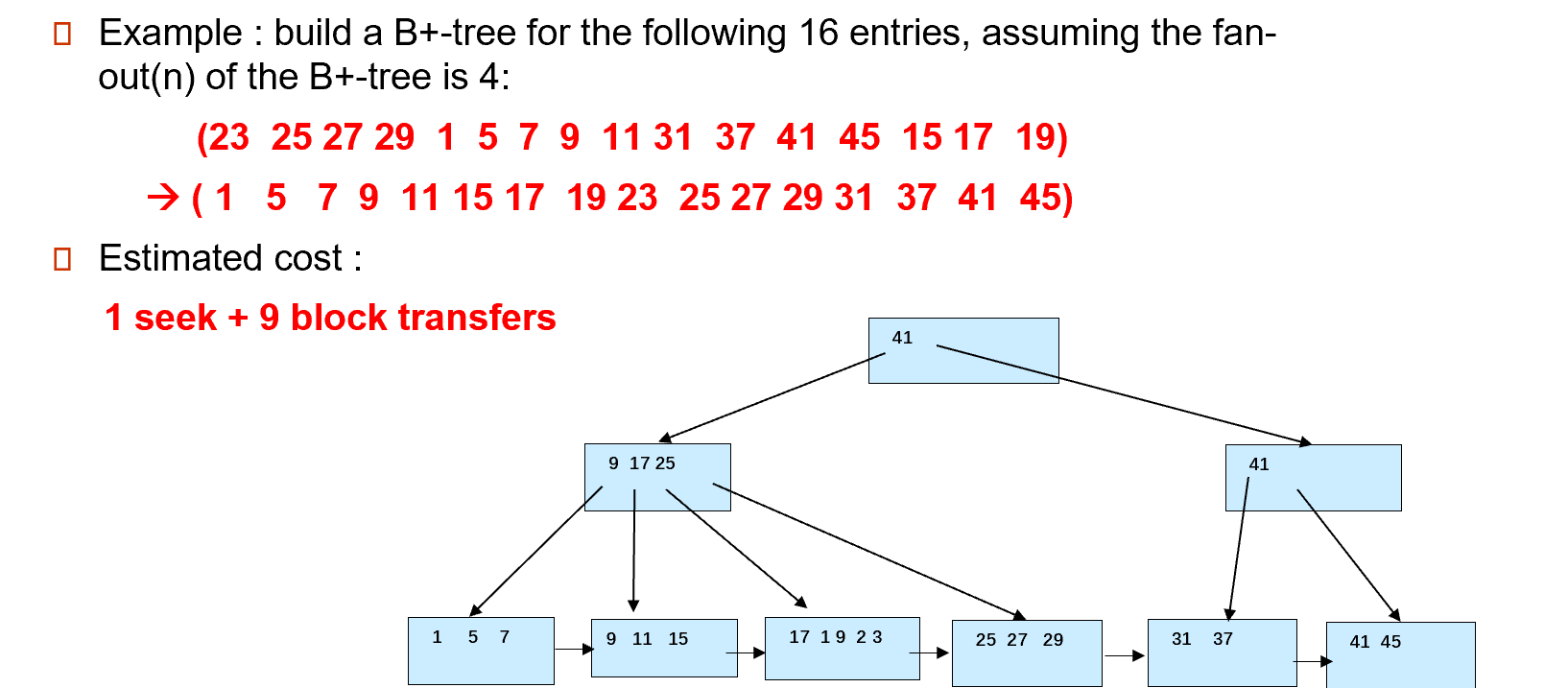
• Efficient alternative 2: Bottom-up B+-tree construction

  • First sort index entries 首先对索引条目进行排序

  • Then create B+-tree layer-by-layer, starting with leaf level

    然后逐层创建 B+-tree，从叶级别开始

  • The built B+-tree is written to disk using sequential I/O operations

    使用顺序 I/O 操作将构建的 B+ 树写入磁盘

存在问题：假如需要排序的索引能够放在内存当中，那么内部排序一次排好。假如需要排序的索引不能放在内存中，那么需要使用外部排序方法。

自底向上构建B+树构建完成后，如何写回到磁盘中？可以一次性写回去，也可以边构建边写回去。

最好的方式：一层一层写回去，从叶子层开始，层序向上遍历。（本质是边构建边写回）

代价：1 seek（定位） + 9 block transfer

这样的好处是：假如我们要顺序访问（扫描或者range query）所有的索引项，这些索引项是全部放在磁盘的同一区域的，且是连续放置的。磁盘读写头只需要一次定位

10.5.2 Bulk insert index entries

批量装载

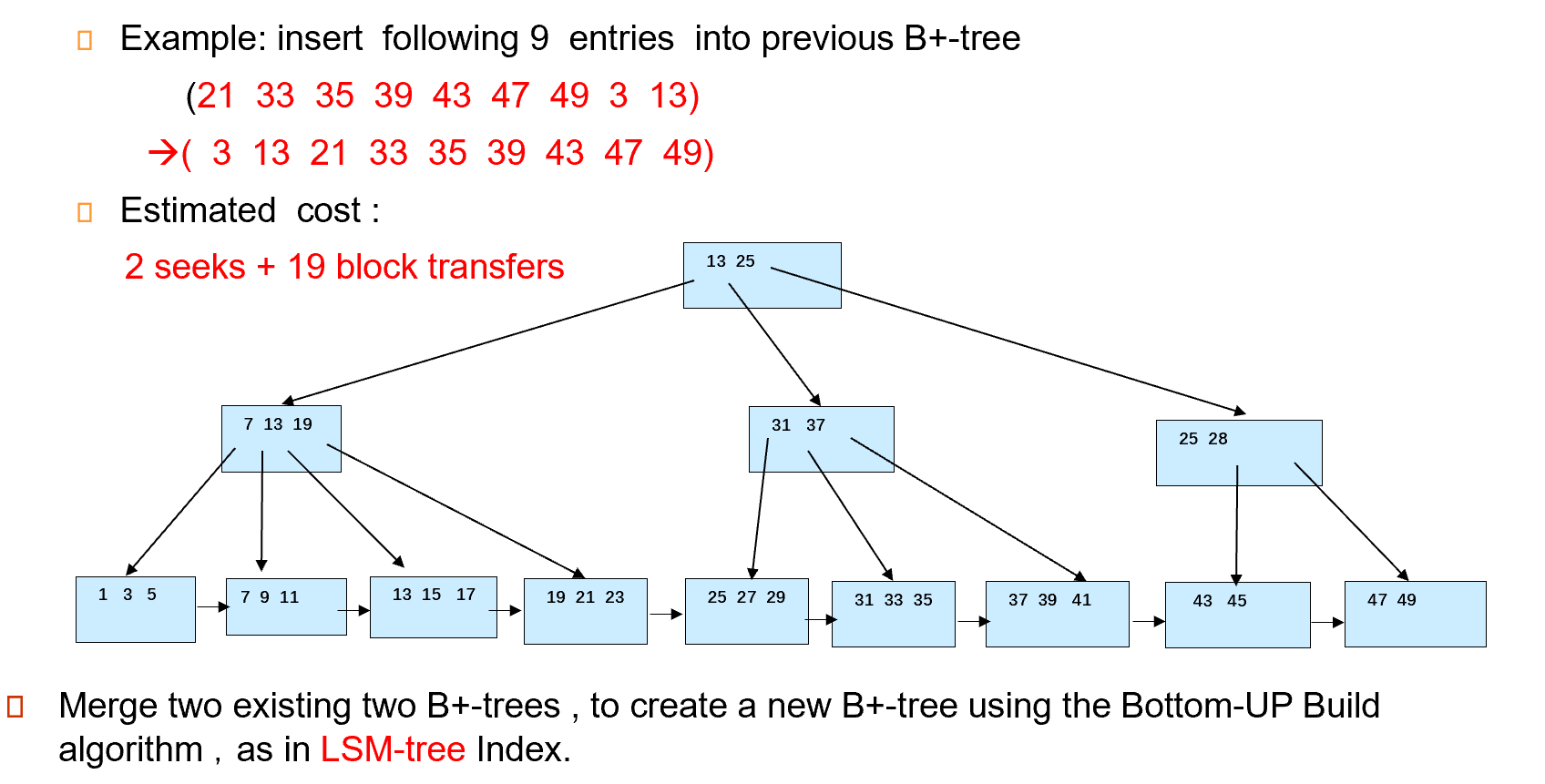
假如有两颗B+树，都是由底向上构建起来的，那么此时如果我们想要Merge这两棵B+树，该怎么办

直接重构一个B+树。先对所有的叶结点的键值进行排序，这两棵B+树的叶子结点都是有序的且连续存放在磁盘中。所以我们对这两棵树的叶子结点的键值分别直接进行一次Seek，再利用mergesort即可

• 第一步：先对这些键值排好序。
• 第二步：从磁盘中读取上一个B+树的所有叶子结点，进入内存当中，由于上一个B+树的叶子结点都是连续存放的，因此需要1次Seek，6次Block Transfer。
• 第三步：利用这些新的键值，和前面那颗B+树已经在内存中的键值，排好序，在内存中构建出新的B+树
• 第四步：把这个处于内存中的B+树按照从底向上层序遍历的顺序，写回到磁盘中，需要1次Seek，13个Block Transfer。

Merge two existing two B+-trees , to create a new B+-tree using the Bottom-UP Build algorithm, as in LSM-tree Index

假设有两棵这样生成的 B+ 树，将他们合并在一起。首先把叶子节点拿出来排序。

10.6 Multiple-Key Access

1. 方法一：分别对dept_name 和 salary都建立索引，查询之后求交集即可
2. 方法二：建立二元组（符合搜索键），词典排序

10.6.1 Indices on Multiple Keys

Composite search keys are search keys containing more than one attribute 复合搜索键是包含多个属性的搜索键

Lexicographic ordering: \((a_1, a_2) < (b_1, b_2)\) if either \(a_1 < b_1\), or \(a_1=b_1\) and \(a_2 < b_2\).

单个 key, 不同 key 之间组合都可以建立 B+ 树。这样会有很多组合，可以在频繁出现的查询属性上建立 B+ 树。

利用复合搜索键构建的B+树，如果仅仅利用第二个属性进行查询，效果往往不适合很好，如上方的salary，所有的数据都是东一块西一块

10.7 Indexing in Main Memory

cache 按 cache line 传输, 只有 64B.

• Random access in memory

  • Much cheaper than on disk/flash, but still expensive compared to cache read

  • Binary search for a key value within a large B+-tree node results in many cache misses

    二分查找可能带来很多 cache miss.

  • Data structures that make best use of cache preferable – cache conscious

    最好利用cache的数据结构 - 缓存意识

B+- trees with small nodes that fit in cache line are preferable to reduce cache misses 最好使用具有适合缓存行的 小节点 的 B+- 树来减少缓存miss

search key 和 pointer 可以分开放。

Key idea:

• use large node size to optimize disk access,

• but structure data within a node using a tree with small node size, instead of using an array, to optimize cache access.

但是使用节点大小较小的树而不是使用数组来构建节点内的数据，以优化缓存访问。

例如，把B+树的结点和指针分开来排列；又例如，把B+树的每一个结点上，建立一个小B+树，用来快速查找键值。

10.8 Indexing on Flash

Flash 里不是即时修改，而是先擦掉再写。同时擦的次数是有限制的。因此最好的方法是从底构建，然后顺序写入。

• Random I/O cost much lower on flash

  20 to 100 microseconds for read/write

• Writes are not in-place, and (eventually) require a more expensive erase 写入不是就地的，并且（最终）需要更昂贵的擦除

• Optimum page size therefore much smaller

• Bulk-loading still useful since it minimizes page erases

  批量加载仍然有用，因为它可以最大限度地减少页面擦除

• Write-optimized tree structures (i.e., LSM-tree) have been adapted to minimize page writes for flash-optimized search trees

写优化索引结构

Two approaches to reducing cost of writes

• Log-structured merge tree (LSM-tree)

• Buffer tree

10.8.1 Log Structured Merge (LSM) Tree

日志归并树

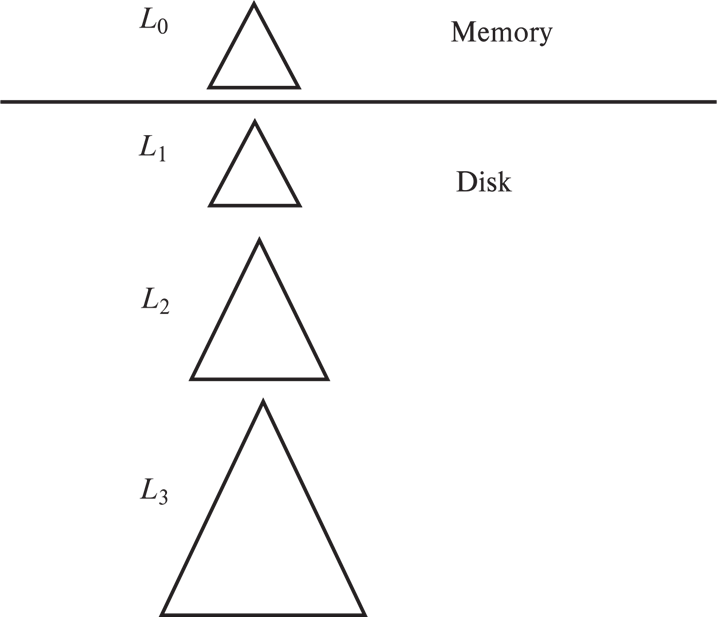
• 首先内存中有一个B+树\(L_0\),内存中的B+树写满之后，马上写入到磁盘中。这个写操作，只需要把B+树叶子结点上的这些块写进磁盘，可以做到刚刚所述的 1次Seek，然后连续写入。
• 下次，内存中的B+树（\(L_0\)）又满了，就可以和磁盘中的B+树(\(L_1\))进行合并，相当于内存中B+树的叶子，要和磁盘中B+树的叶子合并。因此，需要两次Seek，加上合并好的树的结点数目个Transfer + 磁盘中B+树叶节点块数个Transfer。
• 在磁盘中，如果\(L1\)这个B+树满了（磁盘中对各个大小的B+树都有大小限制），那么就会自动拷贝到\(L2\)的位置，把L1的位置空出来，以此类推。
• Size threshold for $L_{i+1}$ tree is $k$ times size threshold for $L_i$ tree

这样我们把随机写变为了顺序写。但此时查找一个索引，就要遍历所有 B+ 树。

• Benefits of LSM approach

  • Inserts are done using only sequential I/O operations

    仅使用顺序 I/O 操作完成插入

  • Leaves are full, avoiding space wastage

    叶子饱满，避免空间浪费

  • Reduced number of I/O operations per record inserted as compared to normal B+-tree (up to some size)

    与普通 B+ 树相比，每条记录插入的 I/O 操作数减少（最多一些大小）

• Drawback of LSM approach

  • Queries have to search multiple trees

    假如我们要查找一个键值，本来我们只需要在一个B+树中查找，现在我们要在L0、L1、L2…这些B+树种，都要查找，查询代价增大。

  • Entire content of each level copied multiple times

    每个level的全部内容被复制了多次

    每次内存种的B+树满了以后都需要合并，合并次数太多。

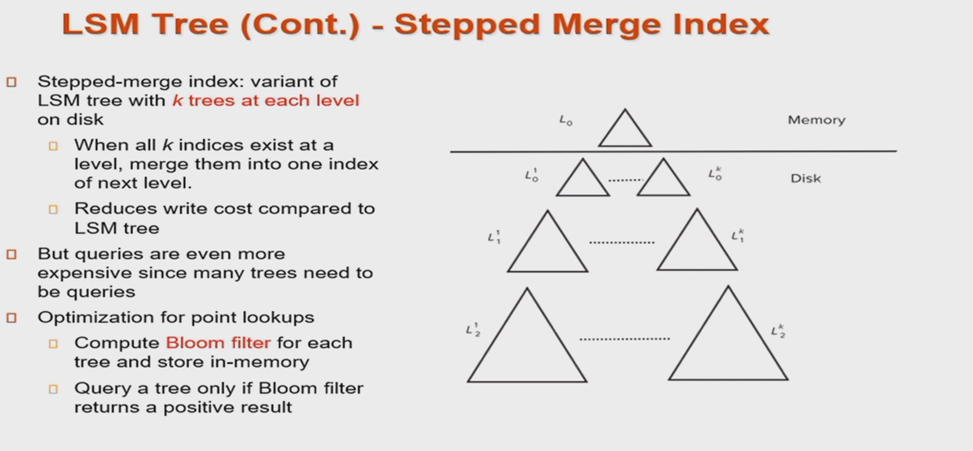
Stepped Merge Index

Stepped-merge index: variant of LSM tree with *k* trees at each level on disk

• When all k indices exist at a level, merge them into one index of next level.
• Reduces write cost compared to LSM tree

But queries are even more expensive since many trees need to be queries

原先的结构中，Merge 操作太多，我们可以一次性合并。

内存中的B+树满了，先写到磁盘中；下次内存中B+树又满了，又写到内存中。直到磁盘中L0级别大小的B+树达到K个以后，再一起合并成一个大的L1。

上述优化结构，虽然减少了Merge的次数，且由于每次合并是顺序访问，减少磁盘I/O的次数；但是缺点是查找更加麻烦(磁盘中B+树的数量更多，因此查找一个键值，需要每一个B+树都查找一遍)。

Bloom Filter

Bloom Filter 相当于对数据的bit进行记录，如果当前位是1，就当检测的对应位置为1，查询时，我们将查询key的值与检测bits进行比对，如果有一位对不上，说明肯定找不到，如果全都对上了，也不一定能找到

为此，可以在磁盘上每一个B+树上加上一个布隆过滤器。每次要查找一个键值时，首先判断一下这个键值可不可能在这棵树中；若不可能，那么这棵树根本不用去查找。

10.8.2 Buffer Tree

• 向B+树中插入一个键值时，不是直接向下传输，传到叶节点中，而是先放在内部节点中的一个小小的Buffer中。

• 缓冲区满了以后，插入的内容会移动到更低的级别，也就是下一层，这一层的子节点的buffer。

• 假如一个buffer tree的内部结点需要分裂，那么缓冲区中的内容也会分裂，各自分裂进入各自的部分。

好处：可以减少查询开销。每次查询有可能不必查询到叶子结点才能得到结果。

坏处：相比LSM树在磁盘中顺序存放的结构,Buffer Tree 的磁盘I/O开销增大。

10.9 Bitmap Indices

适用于大数据分析

查询时只需要进行对应bit数组的AND即可