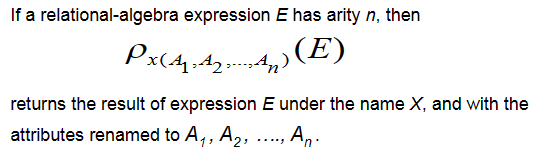2. Relational Model¶

约 2519 个字预计阅读时间 13 分钟

2.1 Structure of Relational Databases¶

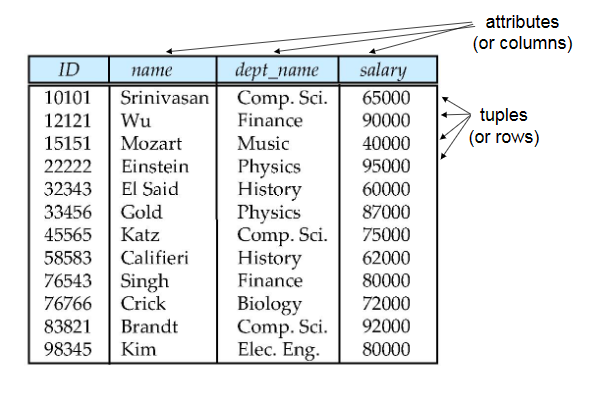
example of a relation

2.1.1 Concepts¶

Formally, given set$D_1, D_2, \ldots, D_n$a relation$r$is a subset of$D_1\times D_2\times \ldots D_n$. Thus a relation is a set of n-tuple$(a_1,a_2,\ldots,a_n)$where each$a_i\in D_i$.

给定集合$D_1, D_2, \ldots, D_n$的关系$r$是$D_1\times D_2\times \ldots D_n$的子集

$A_1,A_2,\ldots,A_n$are attributes.

$R=(A_1,A_2,\ldots,A_n)$is a relation schema.

e.g. instructor = (ID, name, dept_name, salary).

A relation instance$r$defined over schema R is denoted by$r(R)$.

在架构 R 上定义的关系实例$R$用$r(R)$表示

因为关系是一个集合，所以关系都是无序的。

2.1.2 Attributes¶

The set of allowed values for each attribute is called the domain (域)of the attribute
Attribute values are (normally) required to be atomic (原子的); that is, indivisible

属性值要求是原子的，不可分割的，也就是说不能是数组、链表……

The special value null (空值) is a member of every domain

特殊值 null （空值）是每个域的成员

元组的顺序是没有关联的，也就是元组的存放是任意的

2.2 Database Schema¶

Database schema -- is the logical structure of the database.
Database instance -- is a snapshot of the data in the database at a given instant in time.

Example

schema 是抽象的定义, instructor = (ID, name, dept_name, salary). instance 是具体的实例。上述table

2.3 Keys¶

Let$K\subsetneqq R$

$K$is a superkey (超键) of$R$if values for K are sufficient to identify (唯一确定) a unique tuple of each possible relation$r(R)$ e.g.*$\{ID\}$or$\{ID, name\}$

superkey确定，对应的元组唯一确定

Superkey$K$is a candidate key (候选键) if$K$is minimal.
即$K$中没有冗余属性

e.g. $\{ID\}$
One of the candidate keys is selected to be the primary key (主键).

primary key 的值不能为空，且不能重复
Foreign key (外键) Relation$r_1$may include among its attributes the primary key of another relation$r_2$. This attribute is called a foreign key from$r_1$, referencing$r_2$.

外键限制就是关系$r_1$引用的主键必须在关系$r_2$中出现。（在任何数据库实例上，$r1$中每个元组的 A 值也必须是$r2$中某个元组的 B 值。）

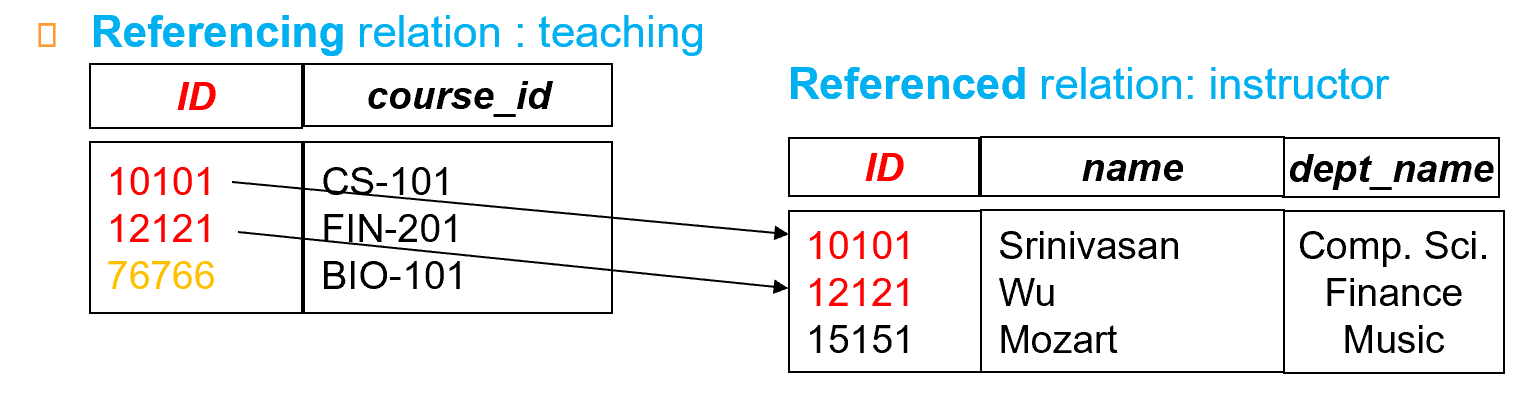
左侧表的老师 ID 必须出现在右侧表中。

Why we need foreign key constraint?

数据库是支持由完整约束条件定义出来的，并维护完整性约束条件。则当我们定义外键后，上述例子中黄色条目是不会出现的。
Referential integrity (参照完整性)

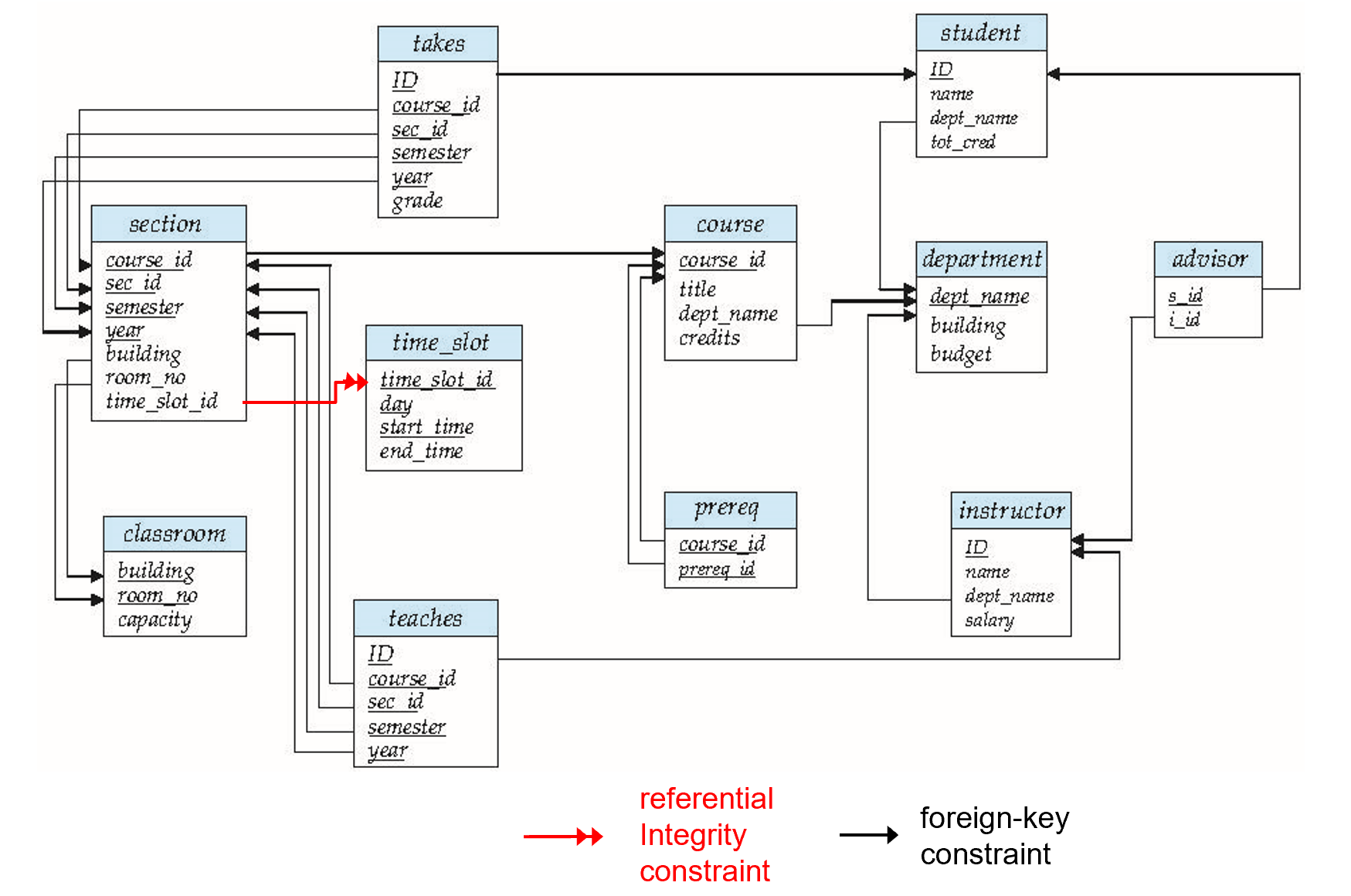
类似于外键限制，但不局限于主键。下图中的time-slot_id并不是Referenced relation的主键

这里$time_slot_id$并不是关系$r_2$的主键，所以这里不是外键限制。

course_id 引用 course中course_id(primary key)

course 指课程信息，无论是否开课，都会有其定义。
section 表示教学班，真正开课时就有相应的实例。（类比于高铁的列车号，和每天对应的班次）
teachers 具体教哪个教学班的老师
takes 表示学生注册课程
time_slot 表示一门课的具体上课时间段，如数据库在周一 3, 4, 5 节; 周一 7, 8 节。
上图中红线表示引用完整性的约束（可以不是主键）；黑线表示外键约束。

2.4 Relational Algebra——relational query language¶

Six basic operators

select:$\sigma$
project:$\Pi$
union:$\cup$
set difference:$-$
Cartesian product(笛卡尔积):$\times$
rename:$\rho$

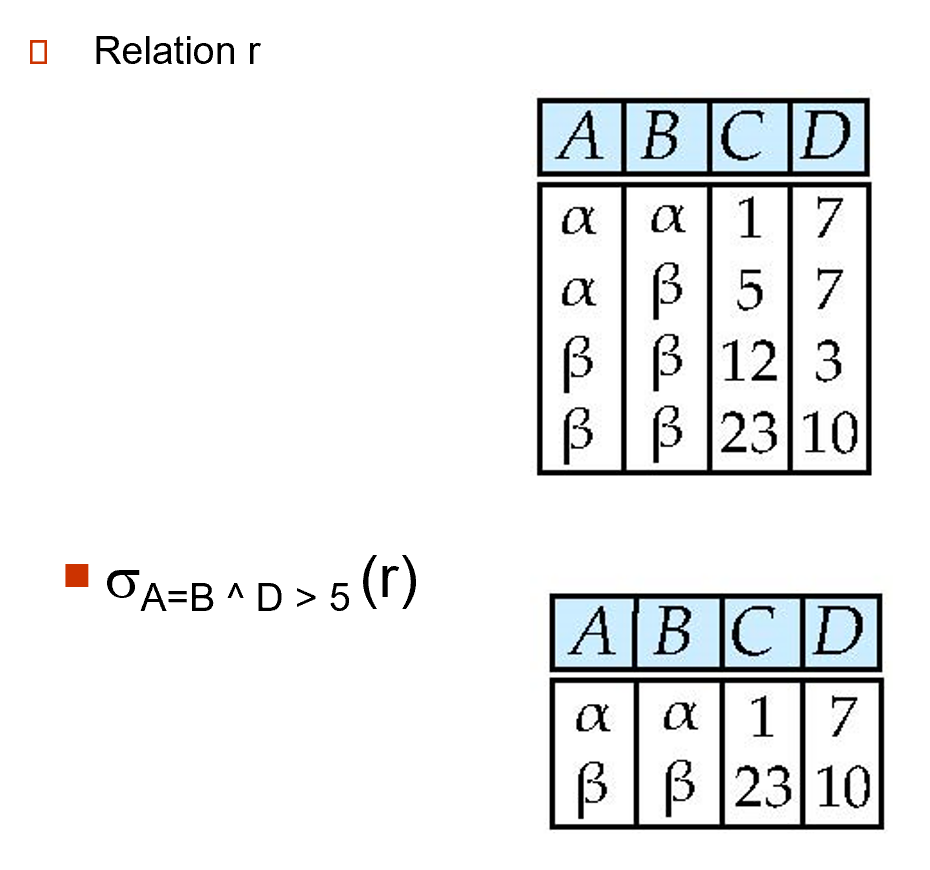
2.4.1 Select¶

$\sigma_p(r)=\{t|t\in r\ and\ p(t)\}$ , where$p$is called selection predicate.

$p(t)$称为选择谓词。

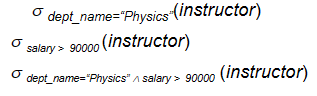
2.4.2 Project¶

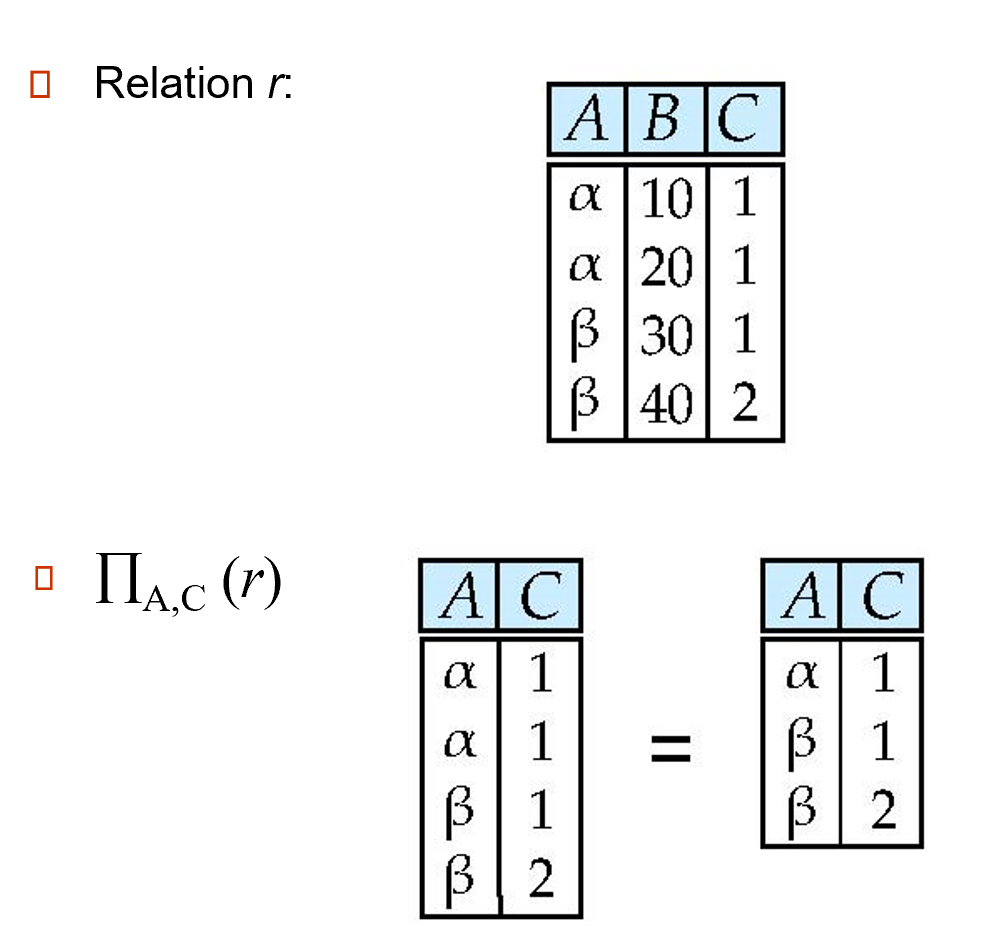
The project operation is a unary operation that returns its argument relation, with certain attributes left out. 项目操作是一个一元操作，它返回其参数关系，省略了某些属性

$\prod_{A_1,A_2,\ldots, A_k}(r)$where$A_i$are attribute names and$r$is a relation name.

The result is defined as the relation of k columns obtained by erasing the columns that are not listed. 会对结果进行去重。

2.4.3 Union¶

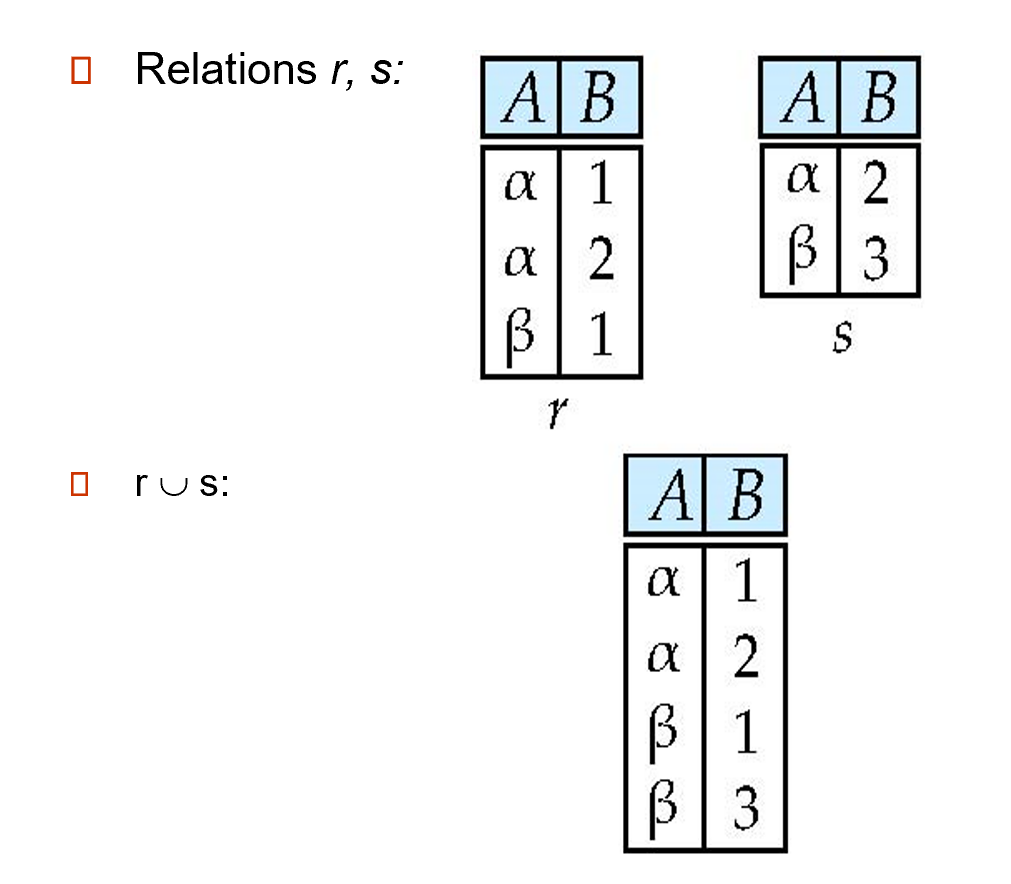
The union operation allows us to combine two relations.

$r\cup s = \{t| t\in r \ or \ t\in s\}$

$r$and$s$must have the same arity (元数) (same number of attributes 相同数量的属性值)
The attribute domains must be compatible .属性域必须兼容 * 当属性有关联类型时，对于每个输入$i$, 两个输入关系的第$i$个属性的类型必须相同。

会对结果进行去重

$\prod _{course_{id}} (\sigma_{semester = "Fall" \wedge year = 2023}(Section))$

2.4.5 Set Difference¶

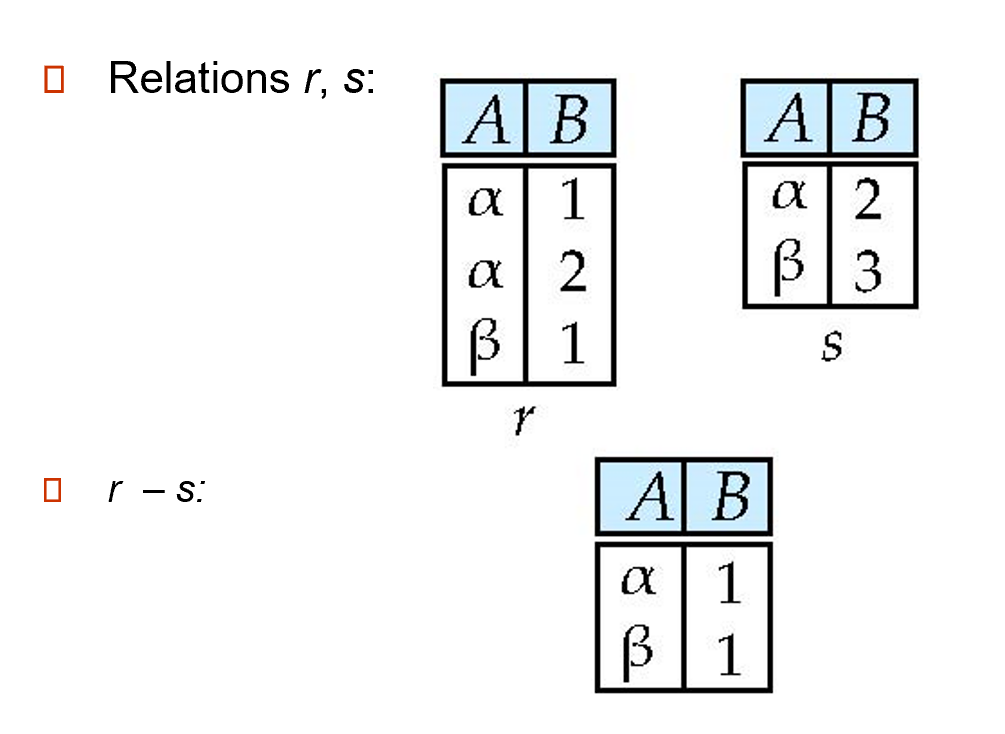
The set-difference operation allows us to find tuples that are in one relation but are not in another.

$r-s=\{t|t\in r\ and\ t\notin s\}$ 我有你没有

$r \cap s = r - (r - s)$

Set differences must be taken between compatible relations.

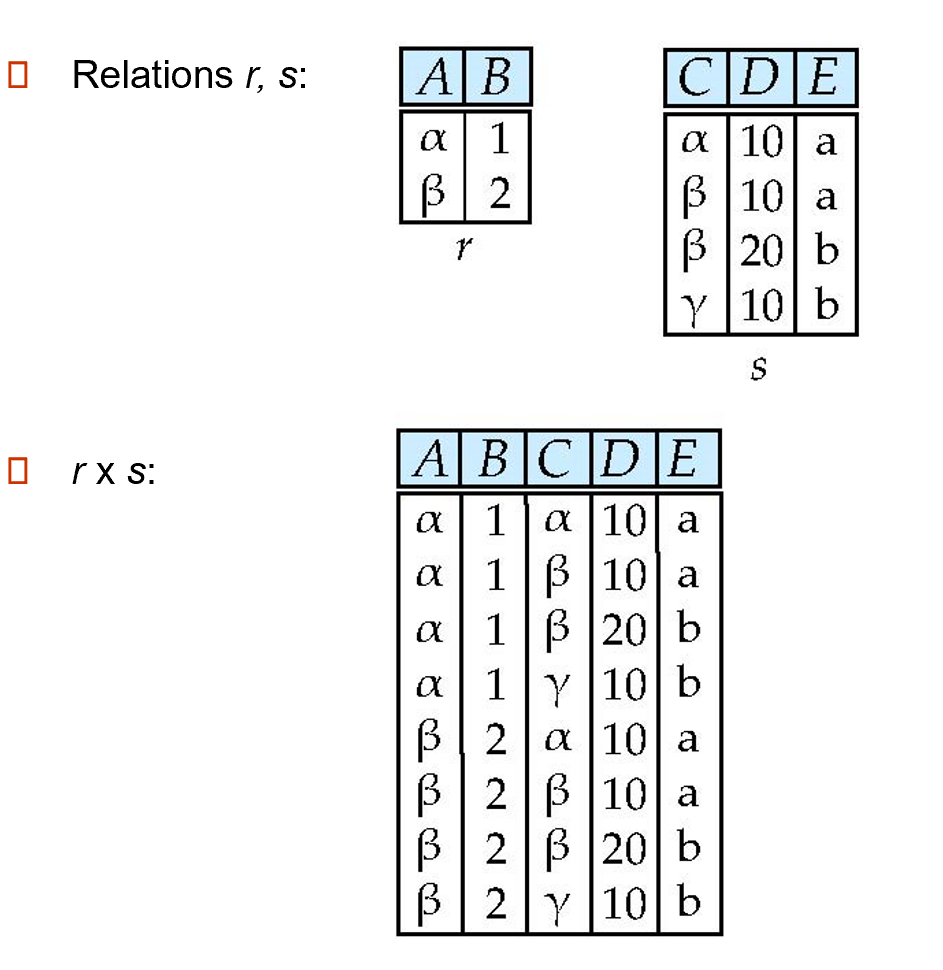
2.4.6 Cartesian-Product 笛卡尔积¶

The Cartesian-product operation (denoted by$\times$) allows us to combine information from any two relations.

$r\times s =\{t\ q|t\in r\ and\ q\in s\}$

2.4.6 Rename=n¶

Allows us to refer to a relation by more than one name. $\rho_X(E)$

返回名称为 X 的表达式 E 的结果，并将属性重命名为$A_1、A_2、...、A_n$。

Find the names of all instructors in the Physics department, along with the course_id of all courses they have taught.

查找物理系所有教师的姓名，以及他们教授的所有课程的course_id。

 这两条语句含义一样，但第二条我们先进行了一次 select, 条目少了更高效。

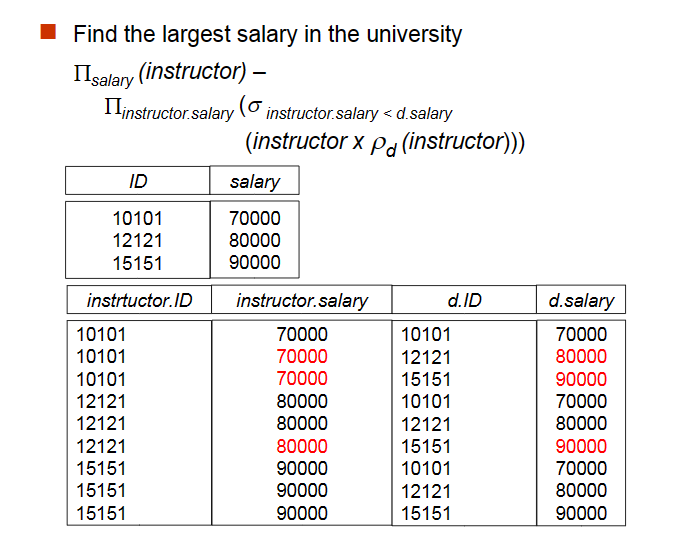
Find the largest salary in the university.

find instructor salaries that are less than some other instructor salary (i.e. not maximum)
using a copy of instructor under a new name$d$.

$\prod_{instructor.salary}(\sigma_{instructor.salary<d.salary}(instructor \times \rho_d(instructor)))$

先列出所有存在小于关系的工资（最高工资不存在小于），进行去重后唯一
find the largest salary

$\prod_{instructor}-\prod_{instructor.salary}(\sigma_{instructor.salary<d.salary}(instructor\times \rho_d(instructor)))$

再利用set difference，找到最高工资

我们第一步将两个关系拼起来之后，限定 instructor 的工资小于 d, 随后投影我们就可以获得所有不是最大值的薪水。（因为任何不是最大值的薪水都会在笛卡尔积 select 后至少存在一个元组，这样投影之后仍会存在。但最大值就不会有元组存在），最后用全集减掉即可。

$E_1 \cup E_2$

$E_1 - E_2$

$E_1 \times E2$

$\sigma_p(E1)$: P is a predicate on attributes in E1

$\prod _S(E1)$: S is a list consisting of some of attributes in E1

$\rho _X(E_1)$: X is the new name for the result of E1

2.4.7 Additional Operations¶

Set intersection:$r \cap s$ r \cap s
Natural join: $r\bowtie s$ r \bowtie s
Assignment:$\leftarrow$leftarrow
Outer join :$r \rtimes s$, $r \ltimes s$,$r$⟗$s$ \rtimes \ltimes
Division Operator:$r \div s$$r ➗ s$

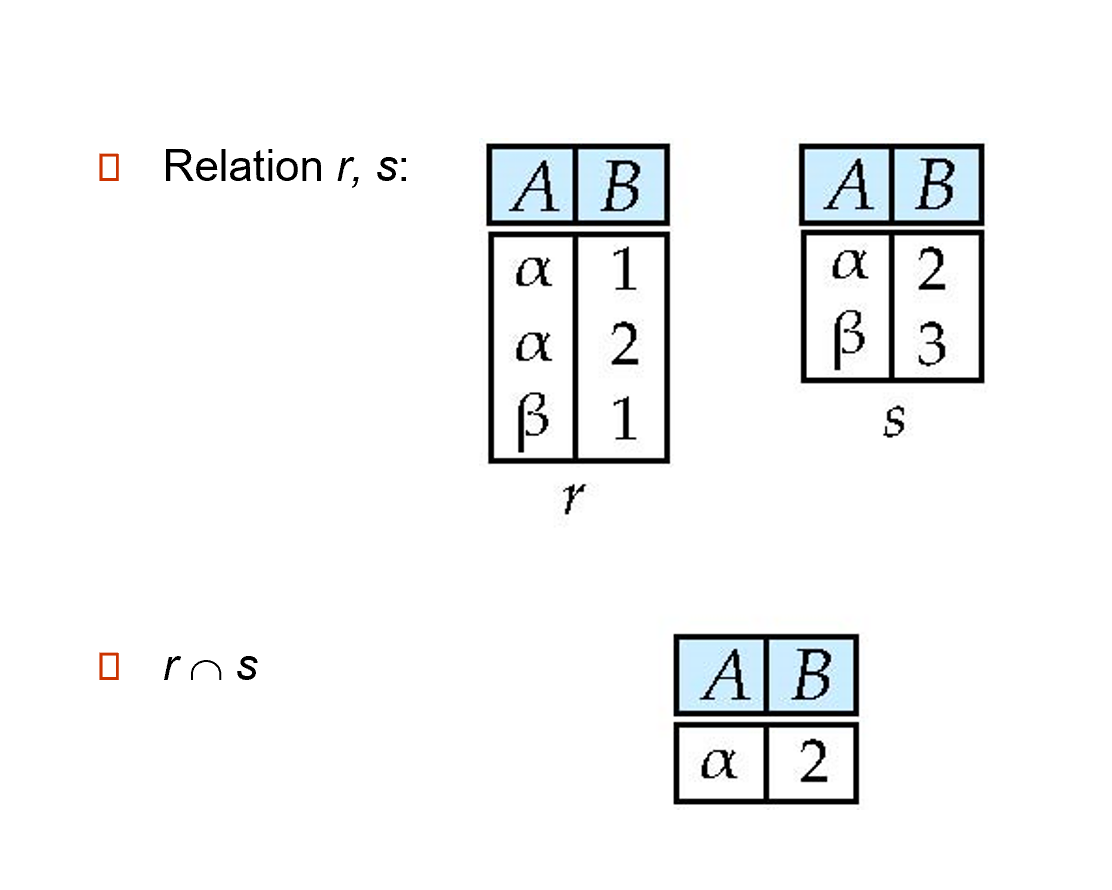
2.4.7.1 Set-Intersection¶

The set-intersection operation allows us to find tuples that are in both the input relations.
$r\cap s=\{t| t\in r\ and\ t\in s\}$

*$r, s$have the same arity * attributes of$r$and s are compatible

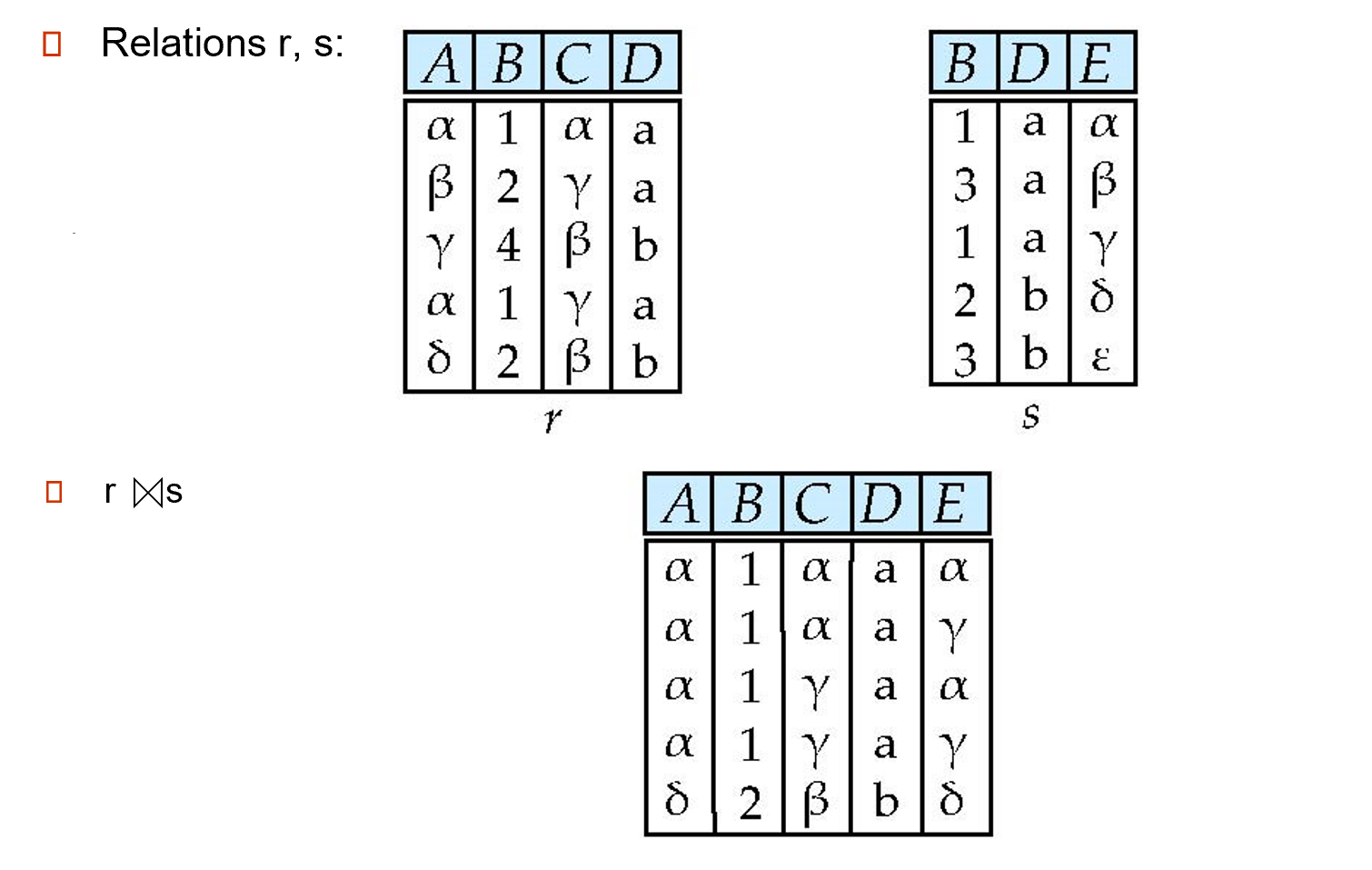
Set-Intersection Operation Example

2.4.7.2 Natural-Join Operation¶

Let r and s be relations on schemas R and S respectively. Then, $r\bowtie s$is a relation on schema$R \cup S$obtained as follows:

Consider each pair of tuples$t_r$from$r$and$t_s$from$s$.
If$t_r$and$t_s$have the same value on each of the attributes in$R \cap S$, add a tuple$t$to the result, where $t$has the same value as$t_r$on$r$ $t$has the same value as$t_s$on$s$

即共同属性要有相同的值，才能在拼接后的结果中保留。

对乘法的扩展，相当于先$\times$再 select, 最后 project.

\[ assiciative: (instructor \bowtie teaches)\bowtie course = instructor \bowtie(teaches \bowtie course) \]

\[ communitative: instructor \bowtie course = course \bowtie instructor \]

\[ \begin{aligned} R &= (A, B, C, D)\\ S &= (E, B, D)\\ result \ schema &= (A,B,C,D,E)\\ r \bowtie s &= \prod_{r_A,r_B,r_C,r_D,s_E}(\sigma_{r.B = s.B \wedge r.D = s.D}(r \times s))\\ 优先保证R和S共有的属性&，具有相同的值，之后再插入s.E \end{aligned} \]

Theta Join $r\bowtie_\theta s=\sigma_\theta (r\times s)$ 条件连接

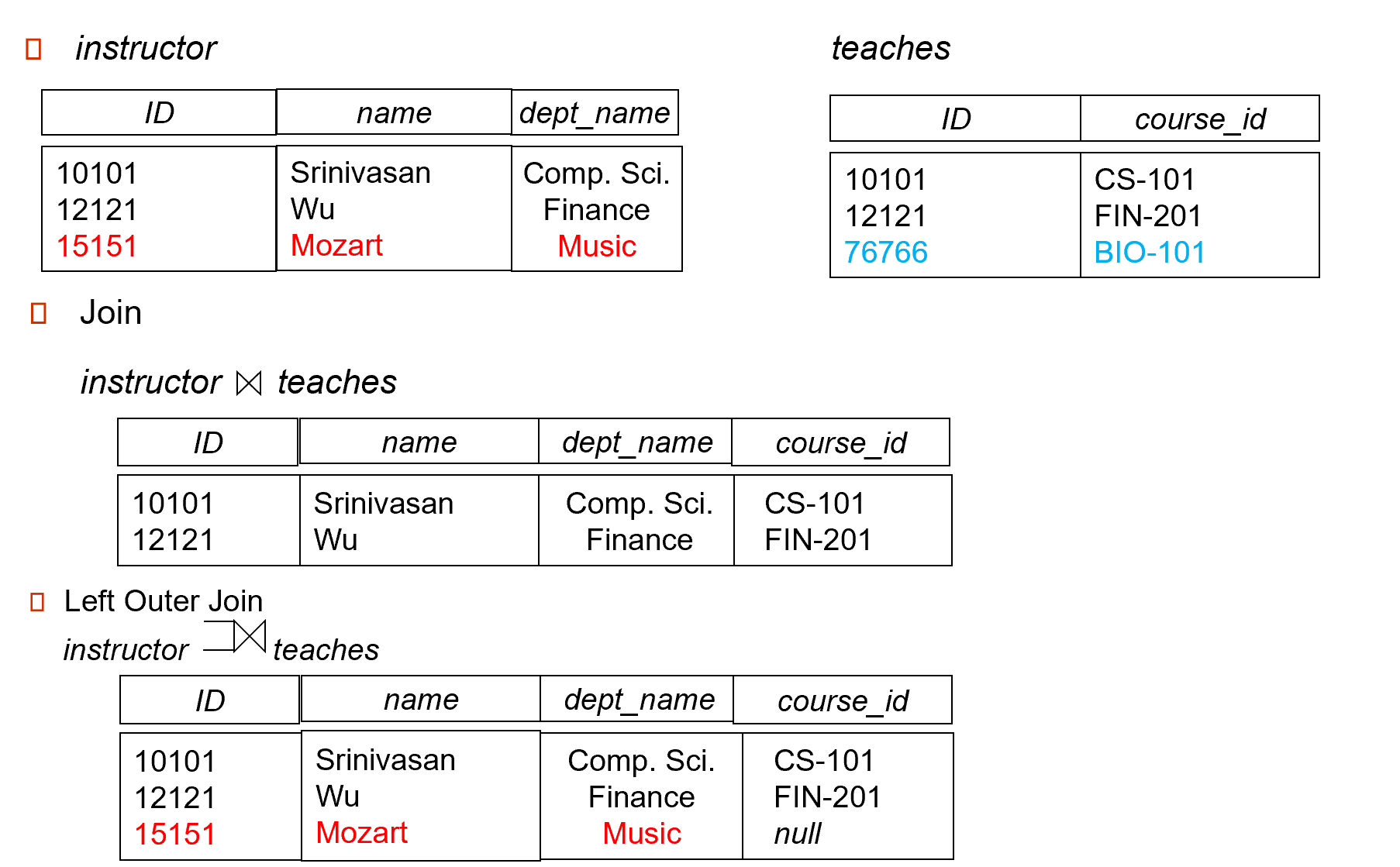
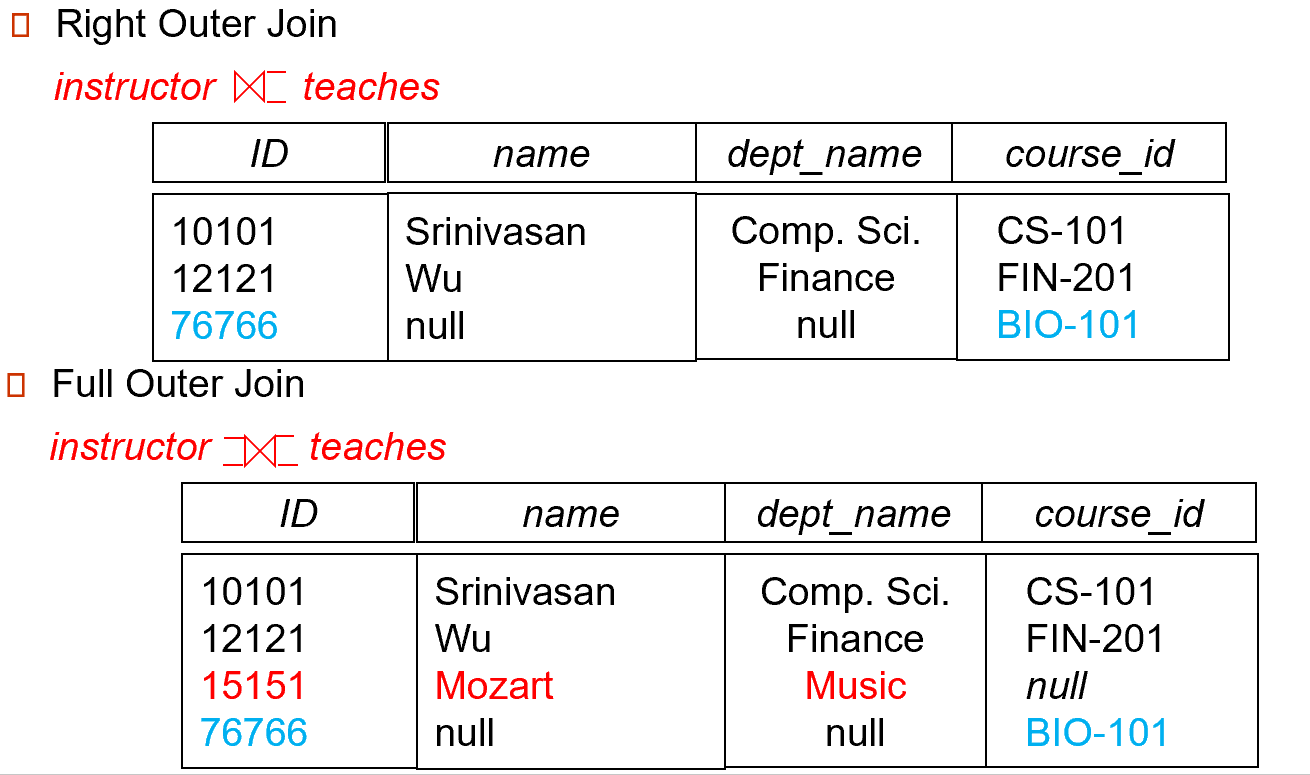
2.4.7.3 Outer Join¶

Computes the join and then adds tuples form one relation that does not match tuples in the other relation to the result of the join.

Uses null values:

null signifies that the value is unknown or does not exist null 表示该值未知或不存在
All comparisons involving null are (roughly speaking) false by definition

普通的join就是natural join，选择共有属性的共有tuple联结

left outer join，左边的table为全集，非共有tuple，value未知补NULL

right outer join，右边为全集，非共有tuple，value未知补NULL

Full outer join，两个table先进行$\cup$,未知的value补NULL

Outer join can be expressed using basic operations.

$r\rtimes s=(r\bowtie s)\cup (r-\cap_R(r\bowtie s)\times \{null,\ldots,null\})$右边补NULL
$r\ltimes s=(r\bowtie s)\cup \{null,\ldots,null\}\times (s-\cap_R(r\bowtie s))$左边补NULL
$r$⟗$s$$=(r\bowtie s)\cup (r-\cap_R(r\bowtie s))\times \{(null, \ldots)\}\cup\{(null,\ldots,null)\}\times (s-\cap_s(r\bowtie s))$

相当于$r⟗s=r \ltimes s \cup r \rtimes s$

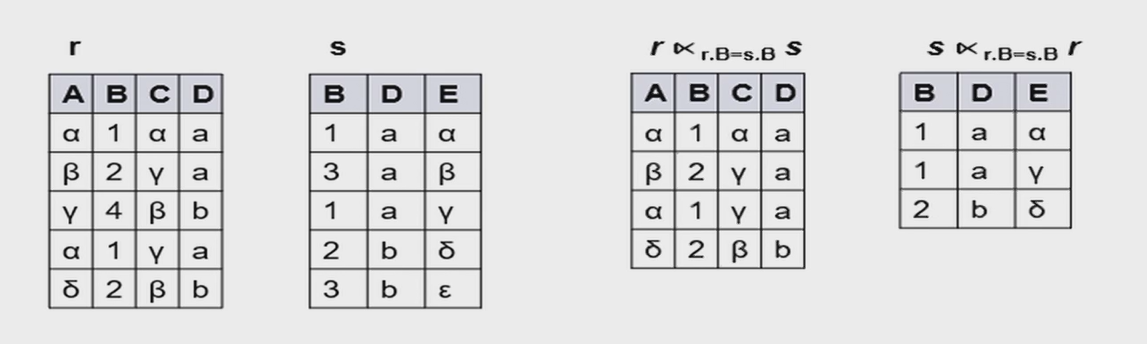
2.4.7.4 Semijoin 半连接¶

$r\ltimes_\theta s$ Is a subset of r, in which every tuple$r_i$matches at least one tuple$s_i$in s under the condition$\theta$.

保留$r$中能与$s$相连的元组。

$$ r \ltimes_{\theta} s = \prod_R(r \bowtie _{\theta} s) $$

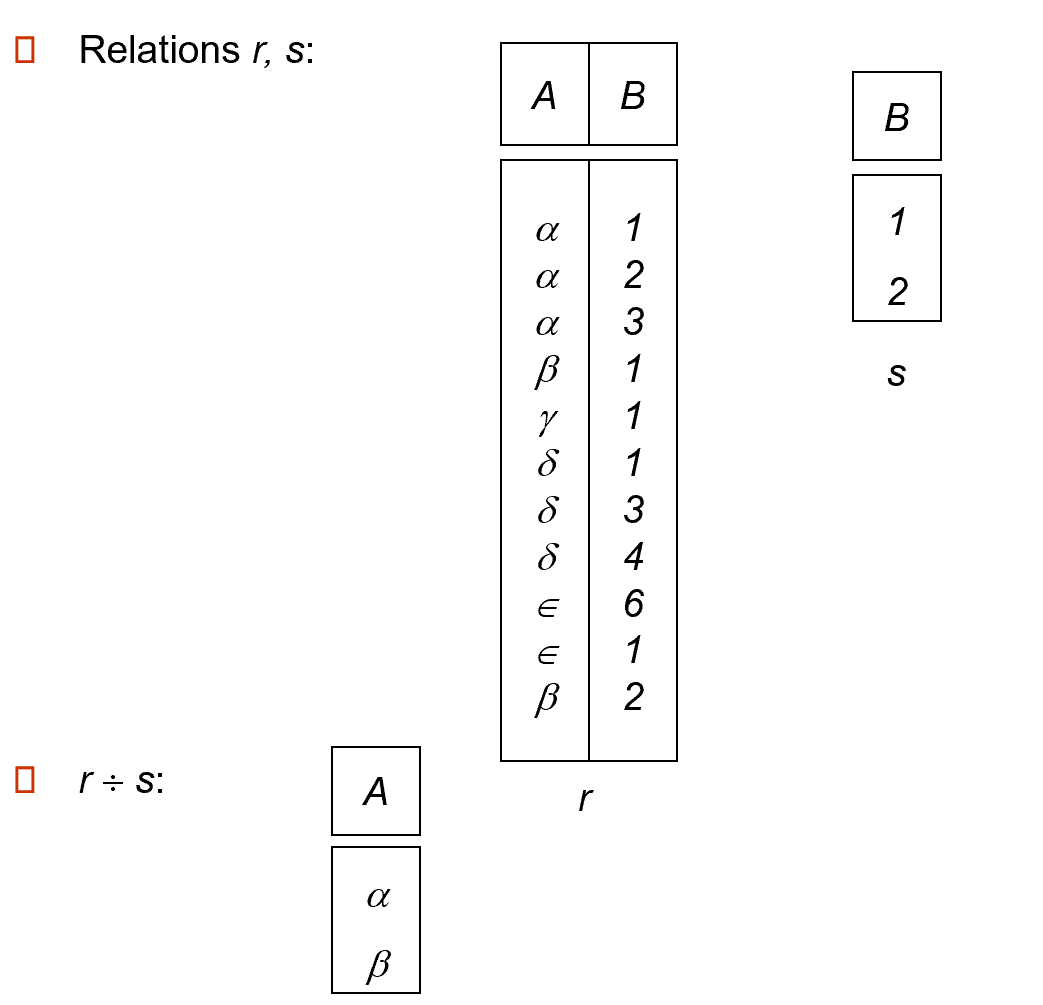
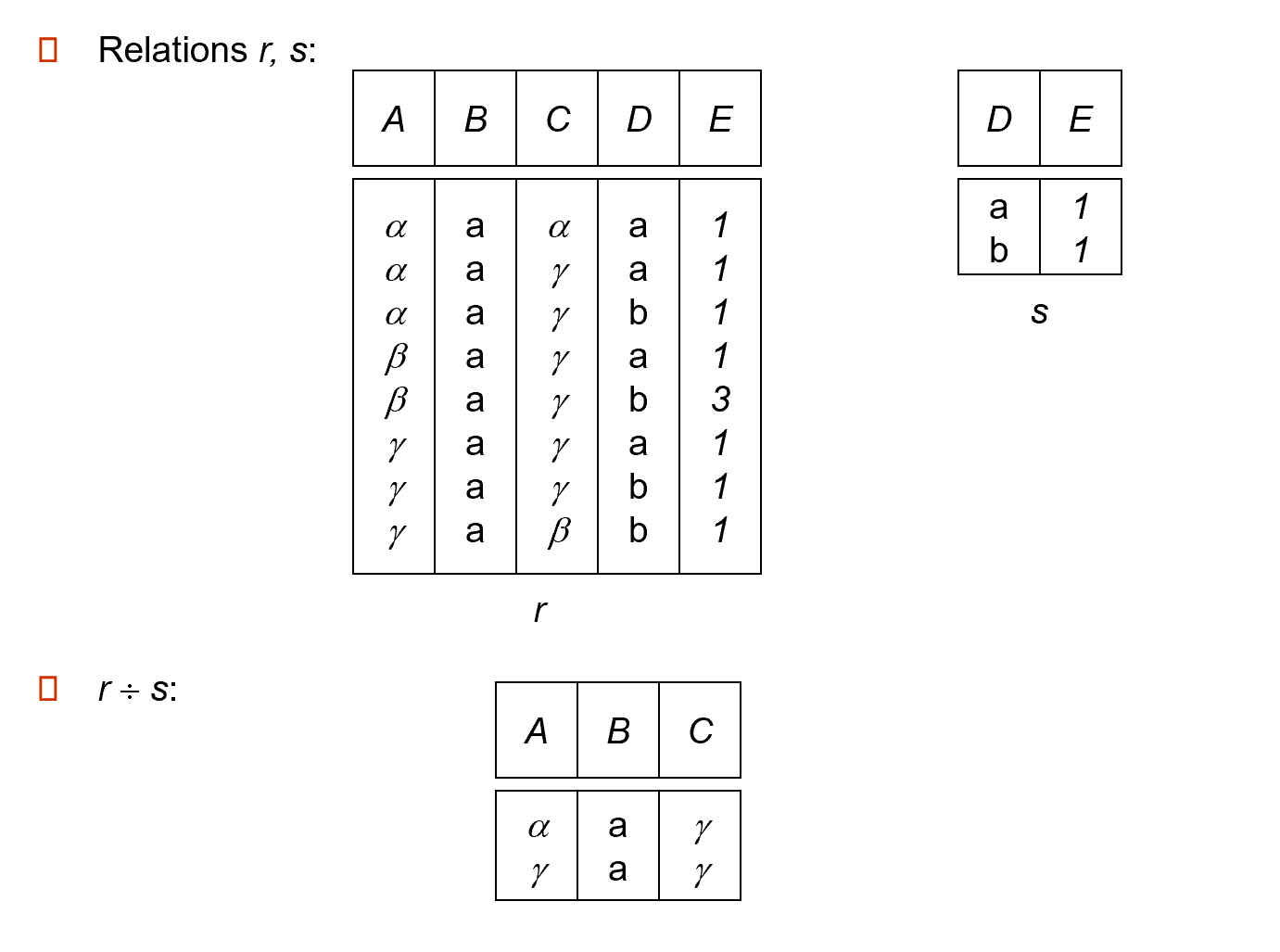
2.4.7.5 Division¶

Given relations$r(R)$and$s(S)$, such that$S \subset R$,$r\div s$is the largest relation$t(R-S)$such that$t\times s \subsetneqq r$

We can write$r\div s$as

\[ \begin{align*} temp1 & \leftarrow \Pi_{R-S}(r)\\ temp2 & \leftarrow \Pi_{R-S}((temp1 \times s)- \Pi_{R-S,S}(r))\\ result & = temp1 - temp2 \end{align*} \]

2.4.8 Extended Relational-Algebra-Operation¶

2.4.8.1 Generalized Projection¶

广义投影: 允许在投影列表使用算术函数来扩展投影操作 $$ \prod_{F_1, F_2,\cdots,F_n}(E) $$

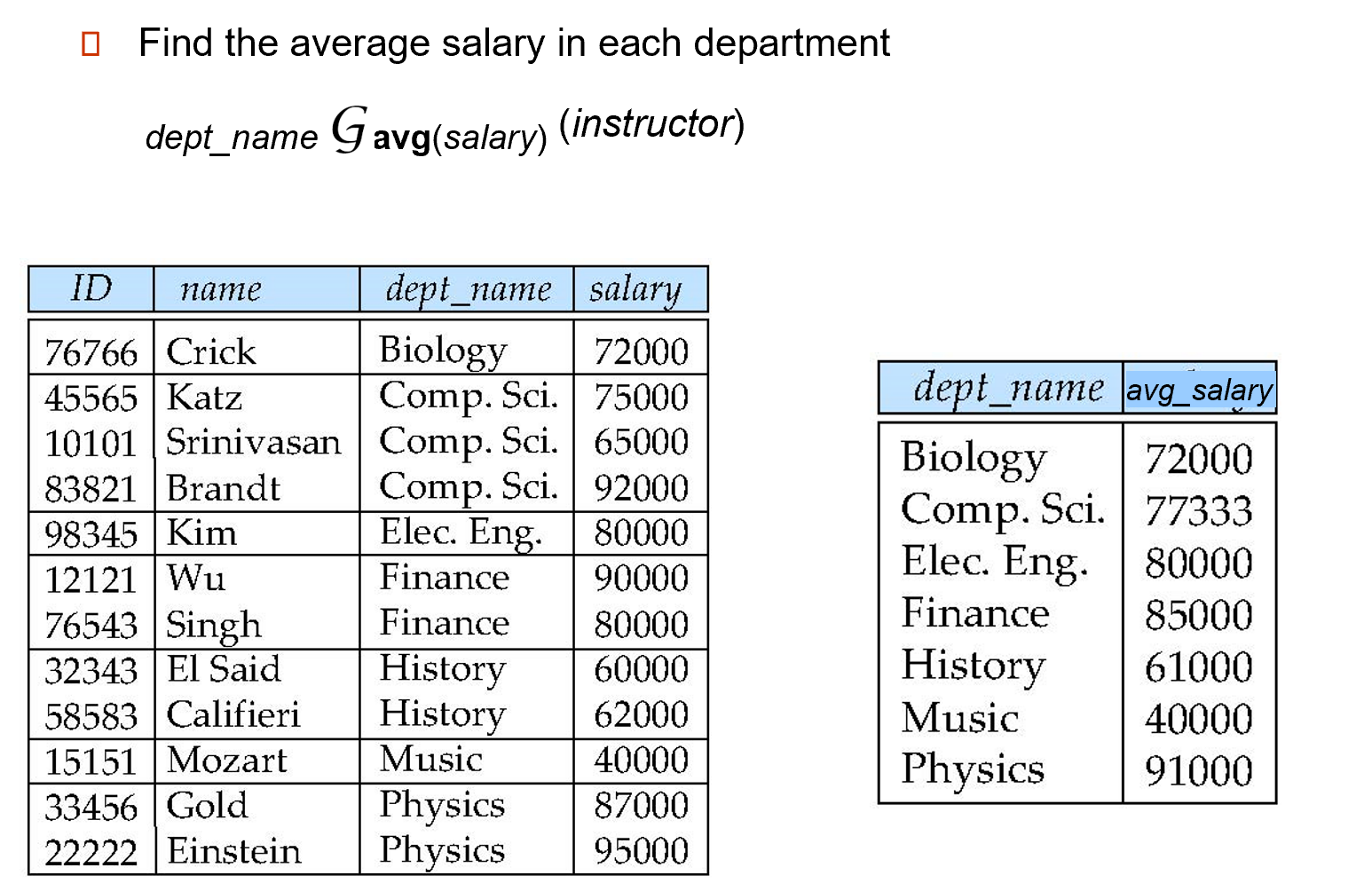
2.4.8.2 Aggregate Functions and Operations¶

Aggregation function（聚合函数）takes a collection of values and returns a single value as a result.
- avg: average value
- min: minimum value
- max: maximum value
- sum: sum of values
- count: number of values
Aggregate operation in relational algebra$G_1,G_2,\ldots,G_n \mathcal{G}_{F_1(A_1),\ldots F_n(A_n)}(E)$

-$G_1,G_2,\cdots,G_n$是目标table的属性，可以为空， -$F_i$是聚合函数，$A_i$是属性名

分组结果没有名字，可以用 rename 或者 as 进行改名。
e.g. dept_name G_ {avg(salary) as avg_sal} (instructor)

2.4.9 Multiset Relational Algebra¶

在纯关系代数中，会删除all duplicates（project 投影）
多重集关系代数会保留重复项
- 对于select：如果元组符合要求，那么元组的重复次数于输入的重复次数相同（也就是全部输出）
- 对于project：即使是重复项，仍然满足元组重复数和输入重复数相等
- 对于笛卡尔积：If there are m copies of t1 in r, and n copies of t2 in s, there are m x n copies of t1.t2 in r x s
- 对于集合操作
  - union： m + n copies
  - intersection： min{m，n}copies
  - difference： min{0，m-n} copies

但实际数据库中并不是，而是一个多重集，允许有重复元素存在。

因为一些操作的中间结果会带来重复元素，要保持集合特性开销很大，因此实际操作中不会去重。

2.5 SQL and Relational Algebra¶

select A1, A2, ... An from r1, r2, ... rm where P is equivalent to$\Pi_{A_1,\ldots, A_n}(\sigma_P(r_1\times r_2\ldots r_m))$
select A1, A2, sum(A3) from r1, r2, ... rm where P group by A1, A2 is equivalent to$A_1, A_2 \mathcal{G} sum(A_3)(\sigma_P(r_1\times r_2\times\ldots r_m))$

这里按$A_1,A_2$分组，那么结果的表中会有$A_1,A_2,sum(A_3)$三列（分组依据+分组后的聚合结果），这里我们需要的就是这三列，所以分组即可。但是假设我们只需要$A_1, sumA3$那么最后还需要投影。